Розміри зубців та вінців зубчастих коліс

Параметри прямо– та косозубих зубчастих передач

ЦИЛІНДРИЧНІ ЗУБЧАСТІ ПЕРЕДАЧІ

Параметри початкового контуру. Згідно з діючими стандартами параметри початкового контуру для циліндричних прямо­та косозубих передач регламентовані такими значеннями (для зубчастих коліс із модулем т ≥ 1 мм): кут головного профілю α = 20°; коефіцієнти – висоти головки зубця h_a^* = 1, радіального зазора

с*= 0,25, висоти ніжки зубця h_f^* = h*_a + c* = 1,25, радіуса кривини перехідної кривої ρ_f ^* = 0,38.

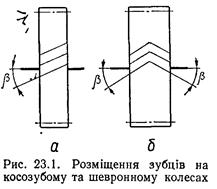
Основною відмінністю косозубих коліс у порівнянні з прямозубими є те, що у косозубих лінія зубців нахилена під деяким кутом β до твірної ділильного циліндра (рис. 23.1, а). Різновидністю косозу­бих коліс є шевронні зубчасті колеса (рис. 23.1, б). Шевронне зубчасте колесо складається як би з двох косозубих коліс, суміщених торцями так, щоб зубці мали протилежний нахил. Косозубі колеса використовують із кутом нахилу зубців β = 8...20°, а у шевронних колесах беруть β = 20...40°, кут нахилу зубців прямозубих коліс β = 0.

Зважаючи на те, що косозубі (ше­вронні) зубчасті колеса можуть нарізуватись таким самим стандартним інструментом, як і прямозубі, кут профілю зубців косозубих (шевронних) коліс у їх нормальному перерізі α_n = α = 20° (відповідно до початко­вого контуру).

За стандартний модуль зубців косозубих (шевронних) коліс беруть модуль m_n також у нормальному перерізі зубців. У пря–мозубих колесах нормальний та коловий модулі однакові: т = т_п = m_t.

Згідно зі значеннями параметрів стандартного початкового конту­ру розміри зубців циліндричних зубчастих коліс (рис. 23.2) визнача­ють за формулами, наведеними у табл. 23.1.

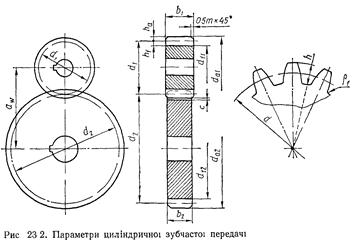
Формули для розмірів вінців циліндричних зубчастих коліс із числами зубців z₁ і z₂, що утворюють зубчасту передачу згідно з рис. 23 2, наведені у табл. 23.2.

Таблиця 23.1 Розміри елементів зубців циліндричних зубчатих коліс

Елементи зубця	Колесо
прямозубе	косозубе (шевронне)
Висота: головки ніжки зубця Радіальний зазор Радіус кривини перехідної кривої	ha – h"а ·m = m hf = (h*+c*) · m = 1,25m h = ha + hf = 2,25m с = c* · m = 0,25m pf = pf* · m = 0,38m	ha = ha* · mn = mn hf =(ha* + c*)· mn= l,25mn h = ha + hf = 2,25mn c = c* · mn = 0,25mn pf = pf* · mn = 0,38mn

Таблиця 23.2. Розміри вінців пари циліндричних зубчастих коліс

Діаметри вінців	Передача
прямозуба	косозуба (шевронна)
Ділильні   Вершин зубців     Впадин	d1 = m · z1; d2 = m · z2   da1 = d1 + 2ha = d1 + 2m, da2 = d2 + 2ha = d2 + 2m;   df1 = d1 – 2hf = dl – 2,5m; df2 = d2 – 2hf = d2 – 2,5m	d1 = mn · z1/cosβ; d2 = mn · z2/cosβ   da1 = d1 + 2ha = d1 + 2mn; da2 = d2 + 2ha = d1 + 2mn;   df1 = d1 – 2hf = d1 – 2,5mn; df2 = d2 – 2hf = d2 – 2,5mn

Міжосьова відстань циліндричних зубчастих передач:

прямозубої а_ω = 0,5 · (d₁ + d₂ ) = 0,5m · (z_l + z₂); (23. 1)

косозубої або (шевронної)

a_ω = 0,5m_n · (z₁ + z₂) / cos β. (23.2)

Враховуючи те, що передаточне число зубчастої передачі u = z₂ / z₁ , ділильні діаметри зубчастих коліс (у некоригованих передачах початкові збігаються з ділильними) можуть бути виражені через міжосьову відстань:

d₁ = 2a_ω / (u ± 1); d₂ = 2a_ω · u / (u ± 1). (23.3)

Тут знак плюс – для передачі зовнішнього зачеплення; знак мінус – для передачі внутрішнього зачеплення.

Ширину зубчастого вінця b₂ колеса (рис. 23.2) потрібно брати залежно від міжосьової відстані передачі

b₂ = ψ_ba · a_ω, (23.4)

де ψ_ba – коєфіцієнт ширини вінця, який беруть: ψ_ba = 0,1...0,4 –для прямозубих передач, ψ_ba = 0,2...0,5 – для косозубих та ψ_ba = 0, 4...0,8 – для шевронних передач. Менші значення ψ_ba вживають при несиметричному або консольному розміщенні зубчастого колеса щодо опор вала, а також при твердості зубчастих коліс Н > 350 НВ.

Граничні значення ψ_ba повинні бути такими, щоб виконувались умови:

ψ_ba = b₂ / d₁= 0,5 ψ_ba (u + 1) ≤ 1 – для прямозубих пере­дач, ψ_ba ≤ 1,5 – для косозубих передач та ψ_ba ≤ 2,5 – для шев­ронних зубчастих передач.

Ширину зубчастого вінця шестірні b₁ беруть на 2 – 5 мм більшою від ширини вінця колеса з метою забезпечення повноти контакту зубців по довжині їх при можливих похибках у монтажі валів пере­дачі в осьовому напрямі.

Коефіціенти торцевого та осьового перекриття. Загальний коефшент перекриття зубчастої передачі

ε_γ =ε_α + ε_β, (23.5)

де ε_α і ε_β – коефіціенти торцевого та осьового перекриття зубців відповідно.

Для зубчастих передач без модифікації зубців і з некоригованими вубцями коефщіент торцевого перекриття можна визначити за такою наближеною залежшстю:

ε_α = [1,88 – 3,2 · (1/z₁ ± 1/z₂,)] · соs β. (23.6)

Тут знак плюс для передач зовнішнього, а знак мінус – внутрішнього зачеплення. У прямозубих передачах (β= 0) рекомендують ε_α ≥ 1,2, а у косозубих

(β ≠ 0) – ε_α ≥ 1.

Коефіціент осьового перекриття ε_β виражаеться відношенням ширини зубчастого вінця колеса b₂ до осьового кроку зубщв Р_х:

ε_β = b₂ / Р_х = b₂ · sin β / Р_n = (b₂ · sin β)/(π · m_n). (23.7)

У прямозубих зубчастих передачах ε_β = 0, а у косозубих переда­чах рекомендують брати ε_β ≥ 1,1, що досягається вибором ширини вшця Ь₂ при заданих β та m_n.

Дата добавления: 2014-01-05