
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Створення планових геодезичних
|
|
|
|
МЕРЕЖ МЕТОДОМ ПОЛІГОНОМЕТРІЇ
Полігонометрія — один з традиційних, найбільш поширених методів створення планових геодезичних мереж усіх класів і розрядів.
Комплекс робіт при створенні планових геодезичних мереж методом полігонометрії складається з таких процесів:
- проектування полігонометричних мереж;
- рекогностування полігонометричних ходів;
- виготовлення і закладання центрів;
- вимірювання кутів;
- вимірювання сторін;
- прив’язка полігонометричних мереж до пунктів вищого класу;
- попередня обробка результатів польових спостережень;
- вирівнювальні обчислення в полігонометрії.
Розглянемо комплекс полігонометричних робіт на прикладі створення мереж згущення 4 класу, 1 і 2 розрядів.
3.1 Проектування полігонометричних мереж
3.1.1 Складання проекту на топографічній карті
Полігонометричні мережі 4 класу, 1 і 2 розрядів створюють для згущення державних планових геодезичних мереж 1, 2 і 3 класів, яких недостатньо для виконання топографічних знімань. Згущення здійснюють до тих пір, поки не буде забезпечена необхідна щільність пунктів, яка забезпечить умови для виконання топографічного знімання.
Полігонометричні мережі 4 класу, 1 і 2 розряду для територій поза населеними пунктами проектують на топографічних картах, як правило, масштабів 1:25000–1:10000, а для територій, що знаходяться в населених пунктах або на будівельних майданчиках — на планах масштабів 1:5000 та 1:2000.
Полігонометричні мережі проектують у вигляді окремих ходів або систем з однією або кількома вузловими точками.
При проектуванні дотримуються технічних вимог “Інструкції” [1].
Вони представлені в табл. 3.1. Проектується прив’язка полігонометричних ходів 4 класу, 1 і 2 розряду до пунктів державної геодезичної мережі. Висячі ходи не допускаються.
Віддалі між пунктами паралельних ходів полігонометрії одного і того ж класу чи розряду повинні бути не меншими у полігонометрії 4 класу — 2.5 км, у полігонометрії 1 розряду — 1.5 км.
При менших віддалях найближчі пункти паралельних ходів повинні бути зв’язані ходами відповідного класу чи розряду [1, п.4.1.4].
Таблиця 3.1 - Технічні характеристики мереж полігонометрії
| Показники | 4 клас | 1 розряд | 2 розряд |
| Гранична довжина ходу, км: окремого між вихідною і вузловою точками між вузловими точками | 14,0 9,0 7,0 | 7,0 5,0 4,0 | 4,0 3,0 2,0 |
| Граничний периметр полігону, км | |||
| Довжини сторін ходу, км: найбільша найменша середня | 3,00 0,25 0,50 | 0,80 0,12 0,30 | 0,50 0,08 0,20 |
| Кількість сторін у ході, не більше | |||
| Відносна помилка ходу, не більше | 1:25000 | 1:10000 | 1:5000 |
| Середня квадратична помилка виміряного кута (за нев’язками у ходах і в полігонах), кутові секунди, не більше | |||
| Кутова нев’язка ходу або полігона, кутові секунди, не більше, де n +1 — кількість кутів у ході | 
| 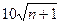
| 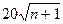
|
| Середня квадратична помилка вимірювання довжини сторони, см: до 500 м від 500 до 1000 м понад 1000 м | 1:40000 | — | — — |
3.1.2 Оцінка проектів окремих полігонометричних ходів
3.1.2.1 Загальні питання оцінки проектів. Видовжені і зігнуті ходи
Запроектовані на карті мережі підлягають попередній оцінці, при якій встановлюється очікувана точність полігонометричних мереж і відповідність її вимогам “Інструкції” [1].
У даному підрозділі ми зупинимося лише на методиках оцінки проектів окремих ходів. Оцінка проектів систем ходів з вузловими точками вивчатиметься на старших курсах при вивченні спеціальних дисциплін.
При оцінці проектів окремих ходів полігонометрії обчислюють очікувану середню квадратичну помилку положення кінцевої точки М. На її величину здійснюють помилки лінійних та кутових вимірів. Якщо позначити сумарний вплив помилок лінійних вимірів mL, а кутових вимірів mu, то для видовженого ходу
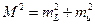 . .
| (3.1) |
Величина впливу помилок лінійних та кутових вимірів на величину М залежить від конфігурації ходу, довжини ходу, довжин сторін, точності кутових і лінійних вимірів.
За конфігурацією окремі ходи поділяються на видовжені, зігнуті і замкнені.
Для того, щоб вияснити, який хід вважається видовженим, а який зігнутим чи замкненим, введемо поняття замикаючої ходу. Замикаюча ходу — це пряма, яка з’єднує початкову і кінцеву точки окремого ходу (рис. 3.1).

Рисунок 3.1 - Полігонометричний хід і його замикаюча
Довжина ходу:

| (3.2) |
де [D х ], [D y ] — суми приростків координат вздовж осей х і y.
3.1.2.2 Критерії зігнутості полігонометричних ходів
Хід вважається видовженим, якщо задовольняються одночасно такі три умови:
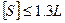 , ,
| (3.3) |
де S — периметр ходу,
L — довжина замикаючої ходу.
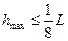 , ,
| (3.4) |
де h max — найбільша віддаль пунктів ходу від замикаючої ходу;
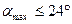 , ,
| (3.5) |
де amax — найбільше кутове відхилення сторін ходу від замикаючої.
Умови (3.3), (3.4) і (3.5) називають критеріями видовженості ходів.
Якщо хоча б одна з трьох умов не задовольняється, хід вважається зігнутим.
Замкнений хід — це один з окремих випадків зігнутого ходу. Оскільки в замкненому ході початкова і кінцева точки співпадають, його замикаюча L =0 (рис. 3.2).
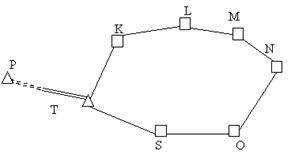
Рисунок 3.2 - Замкнений полігонометричний хід
3.1.2.3 Оцінка проектів видовжених ходів
Розглянемо як впливають помилки лінійних та кутових вимірів на положення кінцевої точки видовженого полігонометричного ходу. Нехай в полігонометричному ході n сторін і n +1 кутів. Якщо допустити, що кожна сторона вимірюється з своєю помилкою, тобто mS 1, mS 2 . .... mSn, то сумарна помилка впливу лінійних вимірів
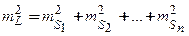
| (3.6) |
Якщо довжини сторін приблизно однакові, а отже виміри рівноточні, тобто
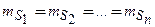 , ,
| (3.7) |
то
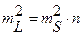 , ,
| (3.8) |
де mS — середня квадратична помилка вимірювання однієї лінії ходу середньої довжини.
Встановимо зв’язок між сумарним впливом кутових вимірів 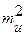 та помилкою вимірювання кутів mb. Розглянемо рис. 3.3
та помилкою вимірювання кутів mb. Розглянемо рис. 3.3
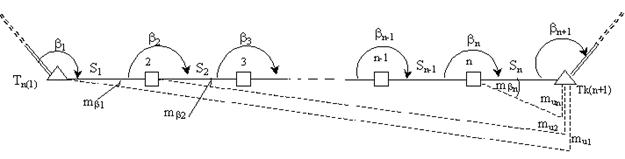
Рисунок 3.3 - Зв’язок між помилками кутових вимірів і
зміщеннями кінцевої точки ходу
Помилка в куті b 1 приведе до зміщення кінцевої точки Тк на величину
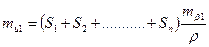 . .
| (3.9) |
Помилка в куті b 2 приведе до додаткового зміщення кінцевої точки Тк на величину
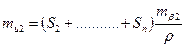
| (3.10) |
і т.д., нарешті під впливом помилки в куті bn точка Тк зміститься ще на величину

| (3.11) |
Сумарний вплив помилок кутових вимірів на зміщення кінцевої точки ходу Тк може бути записаний

| (3.12) |
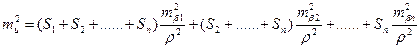
| (3.13) |
При рівноточних вимірах кутів, тобто
 , ,
| (3.14) |
а також приймаючи, що усі сторони приблизно рівні, тобто
| S 1» S 2»..... S» S, | (3.15) |
будемо мати
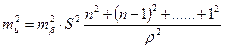 . .
| (3.16) |
Але відомо,що
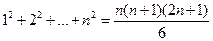 . .
| (3.17) |
Тоді
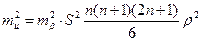
| (3.18) |
Спростимо останній вираз, домноживши чисельник і знаменник правої частини на n. Матимемо

| (3.19) |
Перетворимо член 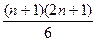 .
.
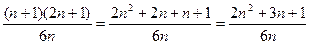
| (3.20) |
Поділимо чисельник і знаменник на 2 n. Отримаємо вираз 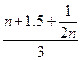 , в якому членом
, в якому членом 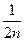 можна знехтувати, врахувавши його малу величину. Таким чином, врахувавши у формулі (3.19), що S×n»L, де L — довжина замикаючої ходу, запишемо
можна знехтувати, врахувавши його малу величину. Таким чином, врахувавши у формулі (3.19), що S×n»L, де L — довжина замикаючої ходу, запишемо
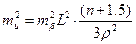 . .
| (3.21) |
Якщо хід прокладений між двома пунктами з вихідними дирекційними кутами, сумарний вплив помилок кутових вимірів буде приблизно вдвоє меншим за рахунок вирівнювання кутів за нев’язку. В цьому випадку формула (3.21) прийме дещо інший вигляд [6]
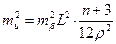
| (3.22) |
Таким чином, формула (3.1) для обчислення очікуваної середньої квадратичної помилки кінцевої точки видовженого ходу прийме вигляд
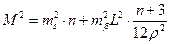
| (3.23) |
У формулі (3.23)
mS — середня квадратична помилка вимірювання сторін, яка в залежності від довжин сторін вибирається з табл. 3.1,
n — кількість сторін,
mb — середня квадратична помилка вимірювання кутів, яка залежить від класу чи розряду полігонометрії і вибирається з табл. 3.1,
L — довжина замикаючої полігонометричного ходу, яку можна визначити з карти графічно, приклавши лінійку до початкової і кінцевої точок ходу.
Після цього обчислюють очікувану абсолютну нев’язку полігонометричного ходу
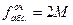 , ,
| (3.24) |
і очікувану відносну нев’язку полігонометричного ходу
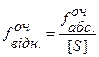 , ,
| (3.25) |
і порівнюють її з граничною відносною нев’язкою, що вибирається з табл.3.1.
Якщо
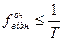 , ,
| (3.26) |
де 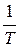 =1:25000 для полігонометрії 4 класу,
=1:25000 для полігонометрії 4 класу,
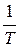 =1:10000 для полігонометрії 1 розряду,
=1:10000 для полігонометрії 1 розряду,
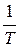 =1:5000 для полігонометрії 2 розряду.
=1:5000 для полігонометрії 2 розряду.
Це свідчить про те, що запроектований хід відповідає необхідним технічним вимогам.
У протилежному випадку хід необхідно перепроектувати, змінивши його параметри (периметр, кількість сторін, середні довжини сторін).
Зауважимо, що формула (3.23) дає наближені результати. Тому замість L у формулу можна підставити [ S ]. Для видовженого ходу [ S ]≤1.3 L, тому другий член формули зросте на 30%. Це приведе до деякого завищення величини М. Якщо при цьому значенні хід відповідає необхідним технічним вимогам, то він тим більше задовольнятиме ці вимоги, коли у формулі використана довжина замикаючої L.
3.1.2.4 Оцінка проектів зігнутих полігонометричних ходів
Очікувана середня квадратична помилка М найбільш слабкої точки зігнутого ходу розраховується за формулою [6]
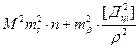 , ,
| (3.27) |
де Дці — віддаль від точки з номером і до центра ваги ходу, координати якого визначаються як середнє арифметичне з усіх точок ходу, а саме
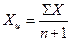 , ,
| (3.28) |
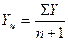 . .
| (3.29) |
Віддаль Дці може бути знайдена як
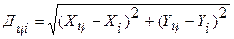 . .
| (3.30) |
Величину Дці можна знайти графічним способом. На карті або на папері в масштабі наносять запроектований хід (рис.3.4). Спочатку визначають центр ваги ходу. Для цього першу сторону ходу ділять наполовину, одержану точку а з’єднують з наступною точкою ходу, отриману лінію ділять на три частини, відмічають точку в, яка віддалена від а на 1/3 лінії, потім точку в з’єднують з наступною точкою ходу і т.д. до кінцевої точки ходу. Після знаходження центру ваги значення Дці знаходять безпосередньо на схемі ходу з графічною точністю.
Потім обчислюють величини Дці, а з їх допомогою 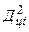 , які сумують і знаходять
, які сумують і знаходять 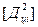 . Цю величину підставляють у формулу (3.27), звідки знаходять спочатку М 2, а потім М.
. Цю величину підставляють у формулу (3.27), звідки знаходять спочатку М 2, а потім М.

Рисунок 3.4 - Визначення центру ваги полігонометричного ходу
графічним способом
Аналогічно до видовженого ходу, обчислюється очікувана абсолютна нев’язка ходу
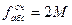 , ,
| (3.31) |
очікувана відносна нев’язка
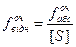 , ,
| (3.32) |
яка порівнюється з гранично допустимою величиною 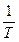 , на основі чого робиться висновок про відповідність запроектованого ходу необхідним технічним вимогам.
, на основі чого робиться висновок про відповідність запроектованого ходу необхідним технічним вимогам.
Дослідження показали, що оцінка проекту зігнутих ходів за формулами 3.23–3.25 дає результати, які незначно відрізняються від результатів, які отримують за формулами 3.27, 3.31, 3.32. Таким чином, для оцінки проектів зігнутих ходів рекомендуємо застосовувати простіші формули 3.23–3.25
3.2 Рекогностування полігонометричних ходів
Рекогностування полігонометричних ходів — це уточнення проекту ходів на місцевості і остаточний вибір місць закладання пунктів.
При рекогностуванні перевіряють взаємну видимість між пунктами і якщо вона відсутня, здійснюють заходи для її забезпечення шляхом усунення перешкод на шляху візирного променя, зміни місця закладання пункту тощо.
Місця для закладання пунктів вибирають так, щоб забезпечувалась їхня непорушність і довготривала збереженість. Тому не можна вибирати місця на зсувних ділянках, на ріллі, на штучних насипах, на проїжджих частинах доріг, на територіях, які підлягають забудові тощо. Пункти повинні бути закладені в таких місцях, щоб візирний промінь проходив не ближче ніж 0.5 м від перешкоди. Для дотримання вимог техніки безпеки пункти полігонометрії не повинні знаходитись дуже близько до колії, ліній електропередач високої напруги тощо.
При виборі місць закладання ґрунтових центрів враховують наявність підземних і наземних комунікацій і майбутню забудову. На забудованих територіях місця закладання полігонометричних пунктів вибирають переважно в фундаментах і стінах капітальних бетонних або цегляних споруд, передбачаючи закріплення їх стінними центрами.
Вибрані на місцевості місця закладання пунктів закріплюють тимчасовими центрами: кілками, металічними стержнями тощо і складають на них абриси з прив’язкою до постійних предметів місцевості.
3.3 Виготовлення і закладання центрів
Пункти полігонометричних мереж закріплюються на місцевості центрами. Центри служать для точного позначення місця розміщення пункта і довготривалого його збереження. Центри можуть мати різну конструкцію, в залежності від фізико-географічних умов їх закладання. Пункти планових мереж закріплюються ґрунтовими, скельними, стінними центрами, а також пунктами на будівлі.
Типи центрів геодезичних мереж регламентуються “Інструкцією про типи центрів геодезичних пунктів” (ГКНТА — 2.01, 02–01–93), ГУГК і К, Київ, 1994 [3]
Зокрема, вузлові пункти полігонометричних мереж 4 класу та суміжні з ними пункти 4 класу закріплюються центрами типу 160 (рис. 3.5).
Ці центри закладаються на глибину, що знаходиться нижче межі промерзання ґрунту на 50 см. Таким чином, висота залізобетонного моноліту становить не менше 120 см.
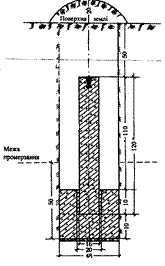
Рисунок 3.5 - Центр пункту полігонометрії 4 класу (тип 160)
Зовнішнє оформлення центру типу 160 виконують обкопуванням квадратної форми з канавою, розміри якої приведені на рис. 3.6
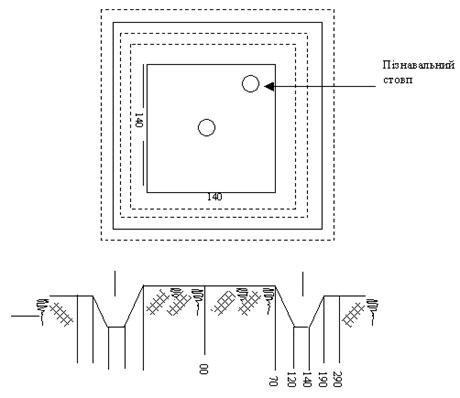
Рисунок 3.6 - Зовнішнє оформлення центру типу 160
Інші пункти полігонометричних мереж 4 класу (тобто не вузлові і не суміжні з вузловими), а також пункти полігонометрії 1 і 2 розрядів закріплюються менш капітальними монолітами, висота яких становить 70–75 см. На незабудованих територіях закладають центр типу У15Н, на забудованих — типу У15 або У15к (див. рис.2.17, 2.18,2.19). Про виготовлення і закладання вказаних типів центрів розповідалось в п.2.3.1.
На забудованих територіях пункти полігонометрії також можуть бути закріплені стінними знаками. Загальний вигляд стінного знаку типу 143 показано на рис 3.7.
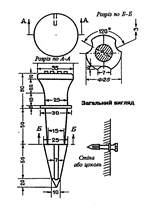
Рисунок 3.7 - Стінний знак типу 143
У стіні або фундаменті капітальної будівлі видовбують отвір, у який на цементному розчині встановлюють стінний знак. Використовувати його для роботи можна не раніше ніж через два дні після закладання.
На забудованих територіях пункти планових мереж усіх класів і розрядів встановлюють також на будівлях. В цьому випадку застосовується конструкція типу У16 що була розглянута в п.2.3.1 (рис.2.16).
3.4 Кутові вимірювання в полігонометричних ходах
3.4.1 Способи кутових вимірювань
Застосовують два способи кутових вимірювань в полігонометричних ходах: спосіб вимірювання окремого кута і спосіб кругових заходів.
Спосіб вимірювання окремого кута застосовується, якщо на пункті два напрямки. В цьому випадку вимірюється кут між двома напрямками.
Якщо на пункті три або більше напрямків, застосовується спосіб кругових заходів. В цьому випадку вибирається початковий напрямок і вимірюються усі напрямки по відношенню до початкового.
Три і більше напрямків вимірюють на вузлових точках, на прив’язках до державних мереж тощо.
3.4.2 Кількість заходів вимірювання кутів
Кількість заходів вимірювання кутів залежить від класу чи розряду полігонометрії та від точності теодоліта. Вона регламентується табл. 3.2.
Таблиця 3.2 - Кількість заходів вимірювання кутів у полігонометрії
| Точність теодоліта | Клас або розряд | ||
| 4 клас | 1 розряд | 2 розряд | |
| 1″ | – | – | |
| 2″ 5″ | – |
3.4.3 Підготовка до вимірів
Кожний захід вимірювання кута виконується на певній частині лімба. Для кожного заходу вимірювання попередньо обчислюється установка лімба, при якій виконується наведення на початкову точку.
Якщо на пункті два напрямки, то за початкову вибирається ліва (задня в ході) точка, якщо три напрями — будь-яка з трьох але як правило вибирають точку з найкращими умовами спостережень.
Між заходами лімб переставляють на величину
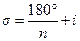
| (3.31) |
або
 , ,
| (3.32) |
де n — кількість заходів, і — ціна ділення лімба теодоліта.
Наприклад, кути вимірюються на пункті полігонометрії 1 розряду трьома заходами.
Тоді 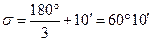 .
.
Отже, установки лімба при наведенні на початкову точку будуть:
у 1 заході 0º10′,
у 2 заході 60º20′,
у 3 заході 120º30′.
Методика встановлення установки лімба для різних типів теодолітів вивчається в курсі “Геодезичні прилади”. Методика приведення теодоліта в робоче положення, наведення теодоліта на візирну ціль і взяття відліків розглянута в п.2.4.2.3 і п.2.4.2.4.
3.4.4 Спосіб окремого кута
Вимірювання окремого кута в одному заході здійснюється 2 півзаходами.
Перший півзахід:
а) наводять попередньо візирну вісь зорової труби при КЛ на ліву (задню у ході) марку, закріплюють алідаду, встановлюють на лімбі розраховану для даного заходу установку (краще встановити відлік на 0.1–0.2′ більший від розрахованого);
б) виконують наведення теодоліта на ліву марку і беруть двічі відлік;
в) виконують наведення теодоліта на праву марку і беруть двічі відлік.
Другий півзахід:
г) переводять трубу через зеніт, наводять теодоліт на праву марку і двічі беруть відлік;
д) виконують наведення на ліву марку і двічі беруть відлік.
При цьому в межах одного заходу алідаду обертають тільки за ходом годинникової стрілки або тільки проти ходу годинникової стрілки.
З двох півзаходів обчислюють середнє значення кута в заході.
Кількість заходів вимірювання кута вибирається згідно з табл. 3.2.
Допуски при вимірюваннях окремого кута в одному заході і між заходами приводяться в табл. 3.3.
Таблиця 3.3 - Допуски при вимірюваннях окремого кута
| Елементи вимірювання | При точності теодоліта | ||
| 1″ | 2″ | 5″ | |
| Різниці в значеннях одного і того самого кута, що отримані з двох півзаходів | 6″ | 8″ | 0′, 2 |
| Коливання значення кута з різних заходів | 5″ | 8″ | 0′, 2 |
3.4.5 Вимірювання напрямків способом кругових заходів
Методика способу розглянута в розділі “Створення планових геодезичних мереж методом тріангуляції” (п.2.4.2.5).
3.4.6 Помилки кутових вимірів у полігонометрії
3.4.6.1 Обґрунтування необхідної точності кутових вимірів у полігонометрії
При обґрунтуванні необхідної точності кутових вимірів виходитимемо з того, що повинна забезпечуватись необхідна точність полігонометричних ходів. Відносна помилка ходу не повинна перевищувати величини 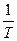 , яка передбачена “Інструкцією” [1], тобто повинна забезпечуватися умова
, яка передбачена “Інструкцією” [1], тобто повинна забезпечуватися умова
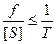 , ,
| (3.33) |
де ¦ — абсолютна нев’язка,
[ S ] — периметр ходу,
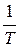 =1/25000 для полігонометрії 4 класу,
=1/25000 для полігонометрії 4 класу,
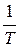 =1/10000 для полігонометрії 1 розряду,
=1/10000 для полігонометрії 1 розряду,
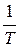 =1/5000 для полігонометрії 2 розряду.
=1/5000 для полігонометрії 2 розряду.
Відомо, що очікувана величина нев’язки
¦=2 М,
де М — очікувана середня квадратична помилка кінцевої точки ходу.
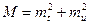
| (3.34) |
Але де mt і mu — середні квадратичні помилки поздовжнього і поперечного зміщень кінцевої точки ходу.
Застосовуючи принцип однакових впливів впливів, тобто допускаючи вплив помилок кутових і лінійних вимірів однаковим, а саме
| mt=mu, | (3.35) |
Запишемо 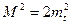
Тоді
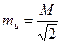 , ,
| (3.36) |
або враховуючи, що ¦ =2 М, а значить 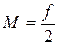 , запишемо
, запишемо 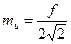
Але з (3.33) граничне значення ¦ запишемо як 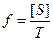 .
.
Тоді 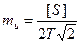
або
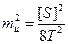 . .
| (3.37) |
Але також відомо з (3.22), що
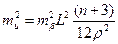 .
.
Прирівнявши (3.37) і (3.22), запишемо
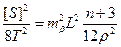 , ,
| (3.38) |
Для видовжених ходів L»[ S ]. З врахуванням цього, отримаємо з формули (3.38)
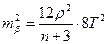
| (3.39) |
або
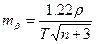 . .
| (3.40) |
Формула (3.40) являє собою залежність між точністю кутових вимірів mb і точністю 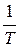 полігонометричних ходів.
полігонометричних ходів.
Виконавши розрахунки за формулою (3.40), знайдемо, що в полігонометрії 4 класу кути необхідно вимірювати з середньою квадратичною помилкою
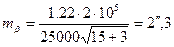 .
.
Тут n =15 — максимальна кількість сторін у ході.
Отримаємо аналогічно для 1-го розряду mb =5″,8, для 2-го розряду: mb =12″,5.
Інструкція [1] вимагає виконувати кутові виміри з середніми квадратичними помилками 3″, 5″ і 10″ у 4 класі, 1 і 2 розряді відповідно.
Відзначимо, що для 4 класу ця точність “Інструкцією” дещо занижена.
3.4.6.2 Джерела помилок кутових вимірів. Обґрунтування величини впливу одного джерела помилок
| На точність кутових вимірів здійснюють вплив такі помилки: | |
| за неточність центрування марки, (помилка за редукцію) | mред, |
| за неточність центрування теодоліта | mц, |
| приладу | mпр, |
| власне виміру | mвл.вим, |
| зовнішніх умов | mзовн, |
| вихідних даних | mвих. |
Якщо допустити принцип однакових впливів, тобто
| m ред= m ц= m пр= m вл.вим.= m зовн= m вих= m і, | (3.41) |
Тоді можемо записати
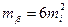 , ,
| (3.42) |
де
mb — середня квадратична помилка вимірювання кута,
mi — середня квадратична помилка впливу одного джерела.
З формули (3.42)
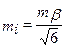 . .
| (3.43) |
Задаючись середніми квадратичними помилками вимірювання кутів у полігонометрії, отриманими вище, за формулою (3.43) обчислимо середню квадратичну помилку впливу одного джерела помилок на вимірювання кутів в полігонометрії 4 класу
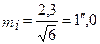 ,
,
в полігонометрії 1 розряду,
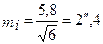 ,
,
в полігонометрії 2 розряду
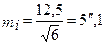 .
.
Враховуючи, що кут складається з 2 напрямків, середня квадратична помилка впливу одного джерела для одного напрямку буде в 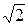 разів менша, тобто становитиме 0″,7; 1″,7; 3″,6 для полігонометрії 4 класу, 1 розряду, 2 розряду відповідно.
разів менша, тобто становитиме 0″,7; 1″,7; 3″,6 для полігонометрії 4 класу, 1 розряду, 2 розряду відповідно.
3.4.6.3 Аналіз впливу окремих джерел на точність кутових вимірів
Помилка за неточність центрування марки (помилка редукції)
Нехай 1 — точка стояння теодоліта над центром пункта 1, 2 — центр пункта 2, на який вимірюється напрямок з пункта 1. М — точка фактичного стояння марки, яка встановлена над точкою 2 з помилкою ml 1, яка на рис. 3.8 зображена відрізком 2 М.
За рахунок помилки центрування марки ml 1 (помилки редукції) замість напряму 1–2 виміряємо напрям 1– М, тобто помилка у виміряному напрямку за редукцію буде виражена кутом mред.
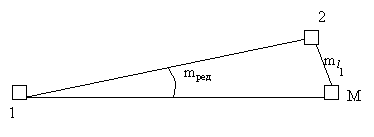
Рисунок 3.8 - Помилка редукції
З рис. 3.8 можемо записати

| (3.44) |
або, враховуючи малу величину кута mред,
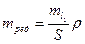
| (3.45) |
Формула (3.45) показує, як впливає помилка центрування марки ml 1, на помилку в напрямі mред.
Задаючись середньою квадратичною помилкою впливу одного джерела на вимірювання напряму, можна встановити середню квадратичну помилку з якого необхідно центрувати марку над центром пункта
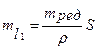 , ,
| (3.46) |
а отже для полігонометрії 4 класу при найбільшій довжині сторони
S =3 км
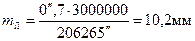
при середній довжині сторони S=500 м
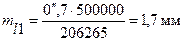 ,
,
при найменшій стороні S=250 м

Точності центрування 1,7 мм і 0,85 мм можна досягнути оптичним виском.
Аналогічні розрахунки можна зробити для полігонометрії 1 і 2 розряду.
Помилка за неточність центрування теодоліта
Нехай 1 — центр пункта 1, 2 — центр пункта 2, на який вимірюється напрямок з пункта 1, Т — точка фактичного стояння теодоліта, який встановлений над точкою 1 з помилкою me, яка на рис. 3.7 зображена відрізком 1 Т.

Рисунок3.9 - Помилка за неточність центрування теодоліта
За рахунок помилки центрування теодоліта me замість напряму 1–2 виміряємо напрям Т-2, тоді помилка у виміряному напрямі буде виражена кутом mц між напрямом Т-2 і напрямом Т-2′, проведеним у точці Т паралельно напряму 1–2.
Цей же кут знаходиться у видовженому трикутнику 1Т2 в точці 2.
Із трикутника 1Т2 запишемо

| (3.47) |
або
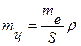 . .
| (3.48) |
Формула (3.48) показує, як впливає помилка центрування теодоліта ml на помилку в напрямі mц.
Задаючись середньою квадратичною помилкою впливу одного джерела на вимірювання напряму, можна встановити середню квадратичну помилку, з якою необхідно центрувати теодоліт над центром пункта
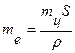 , ,
| (3.49) |
а отже для полігонометрії 4 класу, виконавши розрахунки, як і для помилки редукції, знайдемо що при найбільшій довжині сторони (S =3 км) теодоліт необхідно центрувати з помилкою 10.2 мм, що може бути забезпечено нитяним виском, при середній стороні S =0.5 км з помилкою1.7 мм, при найменшій стороні S =0.25 км з помилкою 0.8 мм, що може бути забезпечено оптичним виском.
Розрахунки для полігонометрії 1 і 2 розряду пропонуємо виконати самостійно.
Триштативна система вимірювання кутів
З метою ослаблення помилок центрування і редукції і зменшення трудомісткості робіт при прокладанні полігонометричних ходів застосовують триштативну систему.
Вона полягає в тому, що на трьох сусідніх точках А, В, С ходу встановлюються три штативи з закріпленими в них трегерами (рис. 3.8).

Рисунок 3.10 - Триштативна система
На задньому А і передньому С встановлюються марки, на середньому В — теодоліт. Після вимірювання кута в т. В, штативи в т. В і т. С з трегерами залишаються в тому ж положенні, а штатив з т. С з трегером переносять в т. D.
Теодоліт виймають з трегера в т. В, переносять і встановлюють в трегер, що залишився на т. С; в трегер, що залишився на т. В встановлюють марку, яку вийняли з трегера в т. А і перенесли на т. В. Марку, яку вийняли з трегера на
т. С встановлюють в трегер на т. D.
Таким чином, якщо прилади попередньо від’юстовані, в точці В вісь обертання марки на наступній станції співпадає з віссю обертання теодоліта на попередній станції, а в точці С — вісь обертання теодоліта на наступній станції співпадає з віссю обертання марки на попередній станції, тобто операція центрування приладів на точках В і С на двох суміжних станціях виконується один раз.
Зменшення кількості операцій центрування приводить до зменшення помилок за центрування приладів і прискорює процес прокладання ходу.
Для прискорення кутових вимірів доцільно мати ще 1–2 запасних штативи з трегерами, які в той час коли виконуються виміри на попередніх точках, центрують з допомогою перевіреного оптичного виска в наступних точках ходу.
Помилка приладу
Помилка приладу залежить від спроможної здатності труби теодоліта та інших його конструктивних особливостей. Величину цієї помилки можна обчислити, виходячи з середньої квадратичної помилки вимірювання кута в одному заході, яка залежить від типу теодоліта, і кількості заходів вимірювання кута.
Формула для обчислення середньої квадратичної помилки приладу має вигляд
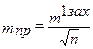 , ,
| (3.50) |
де m 1 зах — середня квадратична помилка вимірювання кута в одному заході теодолітом, згідно з паспортом.
Враховуючи те, що в залежності від типу теодоліта і класу чи розряду полігонометрії, кількість заходів вимірювання кута в кожному випадку різна, складемо таблицю помилок приладу для кожного з цих випадків.
Таблиця 3.5 - Кількість заходів вимірювання кута n (в чисельнику) і середні квадратичні помилки приладу mпр (в знаменнику)
| Клас або розряд полігонометрії | Допустима помилка впливу 1 джерела | n/mпр | ||
| При точності теодоліта | ||||
| 1″ | 2″ | 5″ | ||
| 4 клас | 1″,0 | 4/0″,5 | 6/0,8 | - |
| 1 розряд | 2″,4 | – | 3/1″,1 | 4/2″,5 |
| 2 розряд | 5″,1 | – | 2/1,4 | 3/2″,9 |
З таблиці бачимо, що для усіх випадків, крім одного (застосування теодоліта 5″-ї точності в полігонометрії 1 розряду), помилка приладу не перевищує впливу одного джерела помилок.
Помилка власне вимірювання кута
Процес вимірювання напрямку теодолітом складається з операцій наведення візирної осі на предмет і взяття відліку на горизонтальному крузі.
Середня квадратична помилка власне вимірювання кута mвл.вим може бути знайдена за формулою
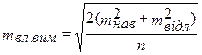
| (3.51) |
де mнавед . — середня квадратична помилка наведення візирної осі на предмет, яка дорівнює
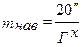 . .
| (3.52) |
Тут Гх — збільшення труби теодоліта, яке становить 30 х для теодолітів типу Т1,
27.5 х для теодолітів типу Т2,
20 х для теодолітів типу Т5,
mвідл . — помилка відліку, яку можна прийняти
0″.2 для теодолітів типу Т1,
0″.5 для теодолітів типу Т2,
0′.1»6″ для теодолітів типу Т5,
n — кількість заходів вимірювання кута, “2” в чисельнику — 2 напрямки, що входять в кут.
Складемо таблицю власне вимірювання кута в залежності від точності теодоліта і класу (розряду) полігонометрії (табл. 3.6).
З табл. 3.6 бачимо, що при вимірюванні теодолітом 1″-ої та 2″-ої точності помилка власне вимірювання кута в 4 класі, 1 і 2 розряді не перевищує допустимого впливу одного джерела, при застосуванні ж 5″-ого теодоліта вона перевищує допустимий вплив одного джерела для 1-го розряду майже вдвоє.
Таблиця 3.6 - Кількість заходів вимірювання кута n (в чисельнику) і середні квадратичні помилки власне вимірювання кута mвл.вим (в знаменнику)
| Клас або розряд полігонометрії | Допустима помилка впливу 1 джерела | n/mвл.вим | ||
| При точності теодоліта | ||||
| 1″ | 2″ | 5″ | ||
| 4 клас | 1″,0 | 4/0″,5 | 6/0″,5 | – |
| 1 розряд | 2″,4 | – | 3/0″,7 | 4/4,0 |
| 2 розряд | 5″,1 | – | 2/0″,9 | 3/5,0 |
З врахуванням висновків до табл. 3.5 і 3.6, рекомендуємо в полігонометрії 1 розряду не застосовувати теодоліти 5″-ої точності, хоча вони передбачені “Інструкцією” [1], а теодоліти 2″-ої точності.
Вплив зовнішніх умов на кутові вимірювання
Значний вплив на точність вимірювання кутів у полігонометрії здійснюють фактори, пов’язані з зовнішнім середовищем, серед яких основними є:
а) рефракція;
б) безпосередня близькість предметів;
в) видимість;
г) коливання зображень.
Рефракція — це заломлення візирного променя, який проходить крізь шари повітря з неоднаковою густиною. Неоднакова густина обумовлена різною підстилаючою поверхнею, різними метеорологічними факторами на шляху променя.
Заломлення променя в горизонтальній площині — це горизонтальна рефракція, у вертикальній — вертикальна. На точність вимірювання горизонтальних кутів здійснює вплив горизонтальна рефракція.
Вплив горизонтальної рефракції на точність кутових вимірів достатньо вивчений, але враховувати його аналітичними залежностями досить складно, в зв’язку з відсутністю даних про розподіл метеорологічних параметрів на шляху візирного променя. Тому ослаблюють вплив горизонтальної рефракції на кутові вимірювання застосуванням спеціальної методики робіт, а саме:
при проектуванні полігонометричних ходів намагаються, щоб на шляху візирного променя в межах кожної сторони не було різких змін метеофакторів;
кутові спостереження виконують в такі періоди доби, коли вплив рефракції мінімальний: це години коли вертикальний температурний градієнт близький до нуля (таке явище починається вранці 0.5 год. після сходу Сонця і триває 1.5–2 год. в сонячну і 2–3 год. в хмарну погоду; і ввечері, приблизно з 16 год. в хмарну і з 17 год. в сонячну погоду і закінчуються за 0.5 год. до заходу Сонця).
Якщо візирний промінь проходить в безпосередній близькості від будівель, інших бетонних, дерев’яних чи металевих споруд, лісових та інших рослинних масивів чи земної поверхні, він заломлюється. Природа цього заломлення приблизно така ж як при рефракції: поблизу цих предметів, які мають іншу температуру, ніж навколишнє середовище, знаходяться шари повітря з іншою густиною.
Щоб уникнути цього заломлення, сторони ходу треба проектувати таким чином, щоб візирний промінь не проходив від будь-яких предметів, рослинних масивів чи земної поверхні ближче ніж на 0.2 м.
Вплив видимості та коливання зображень на точність кутових спостережень в полігонометрії має таку ж природу, як і в тріангуляції (див. п.2.4.6.3).
Якщо вести спостереження в найбільш сприятливі періоди доби, тоді будуть найкращі умови для спостережень і найбільш послаблений вплив на кутові спостереження різноманітних факторів, а саме рефракції, близькості предметів, видимості та коливання зображень.
Такими періодами доби є проміжок часу: вранці, що починається 0,5 год. після сходу Сонця і триває 2–3 год. та ввечері, що починається о 16–17 годині і закінчується за 0,5 год. перед заходом Сонця.
3.5 Вимірювання сторін в полігонометричних ходах
У практиці прокладання полігонометричних ходів на різних етапах розвитку геодезії застосовувалися різні методи вимірювання ліній, основою яких було використання:
- підвісних мірних приладів;
- базисних жезлів;
- оптичних віддалемірів;
- радіовіддалемірів;
- світловіддалемірів або електронних тахеометрів.
Перші чотири групи приладів відіграли в свій час важливу роль при виконанні лінійних вимірів. На сучасному етапі їх використання в полігонометрії, зокрема при створенні мереж згущення (4 класу, 1 і 2 розряду), можливе (при забезпеченні необхідної точності вимірювання ліній) [1], але недоцільне.
Геодезичне виробництво сьогодні забезпечене достатньою кількістю сучасних світловіддалемірів та електронних тахеометрів, які є основними засобами при лінійних вимірах полігонометрії.
Світловіддалеміри та електронні тахеометри — це прилади, в яких вимірювання віддалей здійснюється за допомогою світлових сигналів. Електронними тахеометрами, крім того, вимірюють горизонтальні і вертикальні кути або зенітні віддалі.
Детально світловіддалеміри, електронні тахеометри та методика вимірювання відстаней ними вивчаються в курсах “Геодезичні прилади” та “Електрооптичні та радіогеодезичні вимірювання”.
Тут ми лише коротко зупинимося на питаннях їх точності, в зв’язку з використанням їх у полігонометрії 4 класу, 1 і 2 розрядів.
Згідно з інструкцією [1], при вимірюванні сторін полігонометричних ходів 4 класу, 1 і 2 розрядів треба дотримуватися таких вимог (див. табл. 3.1):
середня квадратична помилка вимірювання довжини сторони
до 500 м — 10 мм,
від 500 до 1000 м — 20 мм,
понад 1000 м — 25 мм· S км.
Вказаної точності можна досягнути при використанні тих чи інших типів світловіддалемірів чи електронних тахеометрів.
Інструкція [1] рекомендує для вимірювання сторін використовувати сучасні світловіддалеміри типів СТ5, 2СТ10, електронні тахеометри Та3М, ТС1010 (Lejca), Elta 50.
Це не виключає можливості використання найсучасніших електронних тахеометрів, які з’явилися в останні роки на світовому ринку, зокрема SOKKIΛ та інші.
Слід відмітити також, що на виробництві сьогодні використовують також інші типи приладів, які були випущені в попередні роки різними фірмами, зокрема, світловіддалеміри: ЕОК 2000, СМ5, 2СМ2, 3СМ2, електронні тахеометри Та5, Та3 (“Агат”), ЕОТ 2000, RECOTA та інші.
Кожен з названих приладів знаходить своє використання в залежності від його далекосяжності та точності вимірів відстаней.
У більшості світловіддалемірів (ТА3М, ТС1010, Elta 50, RECOTA та інших) середня квадратична помилка вимірювання відстаней залежить від довжини ліній і виражається формулою
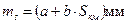 , ,
| (3.53) |
де a і b — постійні величини для даного типу світлрвіддалеміра.
У деяких світловіддалемірів (СМ5, ЕОК 2000), тахеометрів (Та5, ЕОТ 2000) ця помилка від відстані не залежить і виражається величиною
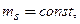
| (3.54) |
де const — постійна величина для даного типу приладу.
У табл 3.7 наведені технічні характеристики деяких типів світловіддалемірів та електронних тахеометрів, які застосовуються в геодезичному виробництві.
Таблиця 3.7 - Технічні характеристики світловіддалемірів та електронних тахеометрів
| Тип приладу | Країна, що випустила прилад | Далекосяжність, м | Середня квадратична помилка вимірювання відстані |
| Світловіддалеміри | |||
| СТ5 | Росія | 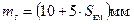
| |
| 2СТ10 | Росія | 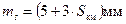
| |
| ЕОК 2000 | НДР | 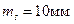
| |
| СМ5 | СРСР | 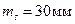
| |
| 2СМ2 | СРСР | 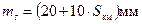
| |
| 3СМ2 | СРСР | 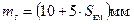
| |
| Електронні тахеометри | |||
| ТаЗМ | Росія | 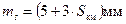
| |
| ТС1010 “Leica” | Німеччина | 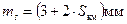
| |
| Elta 50 | НДР | 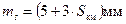
| |
| Та3 “Агат” | СРСР | 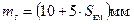
| |
| Та5 | СРСР | 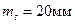
| |
| ЕОТ 2000 | НДР | 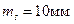
| |
| RECOTA | НДР | 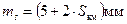
|
Дані табл. 3.7 використовуються при виборі типу світловіддалеміра для забезпечення далекосяжності та необхідної точності вимірювання ліній в запроектованих полігонометричних ходах.
3.6 Прив’язка полігонометричних мереж до пунктів державної геодезичної мережі
Як відомо з класифікації планових геодезичних мереж, мережі 1, 2 і 3 класів відносяться до державних, а мережі 4 класу, 1 і 2 розрядів до мереж згущення. Мережі згущення повинні бути прив’язані до державних. Прив’язка полігонометричних ходів 4 класу, 1 і 2 розрядів до державних передбачає передачу на них координат з пунктів державних мереж та орієнтацію полігонометричного ходу відносно істинного меридіану.
Інструкція [1] передбачає такі варіанти прив’язки полігонометричних ходів 4 класу, 1 і 2 розрядів до пунктів державних геодезичних мереж.
1) Окремий хід полігонометрії повинен опиратися на два вихідних пункти вищого класу, на кожному з яких є видимість як мінімум на один пункт цього ж або вищого класу, а отже є два вихідних дирекційних кути апоч і акінц (рис. 3.11). На вихідних пунктах вимірюють прилеглі кути β 1 і βn+ 1
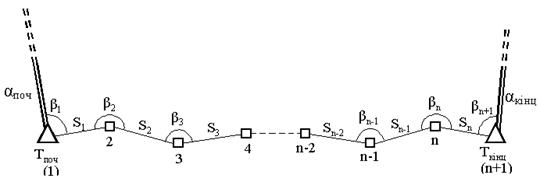
Рисунок 3.11 - Варіант 1
2) Окремий хід полігонометрії опирається на два вихідні пункти вищого класу, на одному з яких відсутня видимість на пункти цього ж або вищого класу і отже є лише один вихідний дирекційний кут і вимірюється один прилеглий кут β 1 (рис. 3.12).

Рисунок 3.12 - Варіант 2
У цьому випадку на пункті Ткінц для контролю кутових вимірів використовують дирекційні кути на орієнтирні пункти, які є на пункті Ткінц . або вимірюють дирекційний кут сторони Sn, астрономічними методами або гіротеодолітами.
3) Окремий хід полігонометрії опирається на два вихідних пункти вищого класу, на яких відсутня видимість на пункти цього ж або вищого класу, отже є лише координатна прив’язка до пунктів геодезичної мережі вищого класу (рис. 3.13).
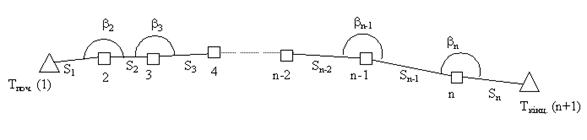
Рисунок 3.13 - Варіант 3
У цьому випадку для контролю кутових вимірів використовують дирекційні кути на пунктах Тпоч . і Ткінц. на орієнтирні пункти або дирекційнні кути сторін S1 і Sn, отримані з астрономічних вимірів або вимірів гіротеодолітами.
4) Окремий хід полігонометрії прокладається у вигляді замкненого, який опирається на пункт вищого класу, на якому існує видимість на пункт того ж або вищого класу (рис. 3.14).
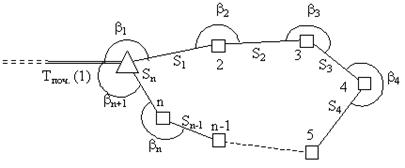
Рисунок 3.14 - Варіант 4
У цьому випадку вимірюються прилеглі кути β 1 і βn+ 1 та визначається дирекційний кут сторони Si, що знаходиться приблизно на середині ходу, астрономічним або гіроскопічним методом.
5) Окремий хід полігонометії прокладається у вигляді замкненого ходу, що опирається на пункт вищого класу, на якому відсутня видимість на пункти того ж або вищого класу. В цьому випадку для контролю кутових вимірів на пункті Тпоч . вимірюється дирекційний кут на орієнтирний пункт або визначається дирекційний кут сторони S 1 астрономічним чи гіроскопічним методом. Крім того, необхідно визначити астрономічним чи гіроскопічним методом дирекційний кут сторони Si, що знаходиться приблизно на середині ходу (рис. 3.15).
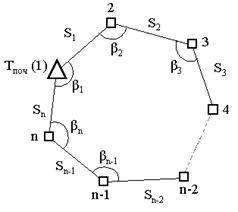
Рисунок 3.15 - Варіант 5
Прокладання висячих ходів не допускається.
3.7 Попередня обробка результатів польових спостережень
Попередня обробка — це проміжний етап робіт, який виконується між польовими вимірами і вирівнювальними обчисленнями. Метою попередньої обробки є оцінка якості польових матеріалів та підготовка їх до вирівнювання. Попередня обробка полігонометричних ходів складається з таких процесів:
- перевірка і обробка польових журналів;
- обчислення ліній, приведених на площу в проекції Гаусса-Крюгера і на рівень моря;
- складання робочої схеми полігонометричного ходу;
- обчислення кутової нев’язки ходу та порівняння її з допустимим значенням;
- обчислення нев’язок координат fx та fy, абсолютної fабс, та відносної fвідн нев’язок та порівняння їх з допустимими значеннями;
- визначення поздовжнього і поперечного зміщень кінцевої точки ходу;
- оцінка точності кутових вимірів;
- оцінка точності лінійних вимірів.
3.7.1 Перевірка та обробка польових журналів
Польові журнали повинні бути належним чином оформлені і перевірені. Усі обчислення, в т.ч. контрольні, виконують у дві руки. Якщо при кутових та лінійних вимірюваннях використовувалися електронні геодезичні прилади та персональні комп’ютери, то виконують обробку результатів вимірювань, знятих з реєстраторів чи накопичувачів інформації.
3.7.2 Обчислення ліній, приведених на рівень моря і на площину в проекції Гаусса-Крюгера
У довжини ліній, які приведені до горизонту, вводять поправку за приведення на рівень моря за формулою
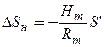 , ,
| (3.55) |
де Hm — середня висота лінії над рівнем моря, яка обчислюється як середнє арифметичне з висот кінців лінії

| (3.56) |
Rm — радіус кривизни земного еліпсоїда в точці m, що лежить посередині лінії, він обчислюється за формулами, які вивчаються в курсі вищої геодезії або знаходиться за спеціальними таблицями як функція широти точки, S' — лінія виміряна і приведена до горизонту.
Оскільки в Україні від’ємні висоти точок земної поверхні на суші відсутні, поправки Δ SH завжди будуть від’ємними.
Поправку за редукування лінії на площину в проекції Гаусса-Крюгера обчислюють за формулою
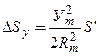 , ,
| (3.57) |
де Уm – віддаль точки m, що лежить посередині лінії, від осьового меридіана.
Хоча віддаль Уm може бути як додатною так і від’ємною, але оскільки у формулі (3.57) вона знаходиться у квадраті, величина Δ Sy завжди буде додатною.
3.7.3 Складання робочої схеми полігонометриного ходу