Коливальний рух. Вільні й вимушені механічні коливання. Гармонічні коливання. Зміщення, амплітуда, період, частота і фаза гармонічнихколивань

Тема 15. Коливання та хвилі

Коливання та хвилі (2 год)

Мета: Дати означення коливанням.Визначити закони коливання маятнику.

План 1. Загальна характеристика гармонічних коливань. 2. Пружинний, математичний та фізичний маятники. 3. Вільні коливання в контурі без активного опору.  

Коливаннями або коливальними рухами називають такі види механічного руху чи зміни стану системи, які періодично повторюються в часі, наприклад, механічні коливання тіла на пружині, коливання маятників, коливання струн, вібрації фундаментів будівель, електромагнітні коливання в коливальному контурі.

За фізичною природою коливання поділяють на механічні та електромагнітні, за характером коливань - на вільні, вимушені та автоколивання. Хоча коливання досить різноманітні за своєю фізичною природою, але вони мають спільні закономірності й описуються однотипними математичними методами.

Механічні коливання - періодичне зміщення тіла то в один, то в другий бік відносно положення рівноваги.

Механічна система, в якій одне або декілька тіл можуть здійснювати коливальні рухи, називають коливальною системою.

Коливання, які відбуваються лише під дією внутрішніх сил, називають вільними. Щоб система виконувала ці коливання, треба вивести тіло з положення рівноваги, тобто надати коливальній системі енергію. При цьому рівнодійна всіх сил, що діють на тіло, має бути відмінною від нуля і спрямованою до положення рівноваги, в якому рівнодійна дорівнює нулю. Вільні коливання виникали б, якби не було впливу зовнішніх сил. Цього досягти неможливо, тому вільні коливання це абстракція. Вони з часом стають згасальними.

Виникла потреба в коливаннях під дією зовнішньої сили, що періодично змінюється, такі коливання називають вимушеними. Ці коливання здійснюють поршні в циліндрах двигунів, голка швацької машини тощо.

Ще одним видом незагасальних коливань є автоколивання. Це коливання, які підтримуються внутрішніми джерелами енергії системи, коли не діє зовнішня періодична сила. Наприклад, настінний годинник з маятником або наручний механічний годинник - це механічні автоколивальні системи.

У годинниках потенціальна енергія тягарця (або стиснутої пружини) поступово, окремими порціями передається маятнику і компенсує втрати на тертя. Можна спостерігати автоколивання струни під дією смичка, голосових зв'язок під час розмови або співу.

Коливання називають періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через однакові проміжки часу. Найпростішим прикладом періодичних коливань є гармонічні коливання, під час яких фізична величина змінюється з плином часу за законом

x = A sin(w t + j₀), або x = A cos(w t + j₀), (5.1.1)

де А, w, і j₀ - постійні величини, причому А > 0, w > 0.

Найпростіший приклад гармонічного коливання - це коливання вздовж осі Ох проекції кінця радіуса-вектора точки, що рухається по колу радіуса А (рис.5.1.2). Якщо t = 0 радіус вектор ОВ утворює з віссю Оу кут j₀, а за час t описує кут w t, так що в довільний момент часу x = A sin(w t + j₀).

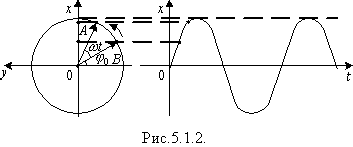
У механічних коливаннях х - зміщення тіла (коливальної системи) від положення рівноваги. У СІ [ x ] = м; А - амплітуда - найбільше відхилення від положення рівноваги. Якщо коливання незагасальні, то амплітуда не змінюється. У СІ [ А ] = м.

Мінімальний проміжок часу Т, через який повторюється певне значення змінної величини, що характеризує коливальну систему, називають періодомколивань. Або ж простіше: період - це час одного повного коливання. Якщо за час t відбулося N коливань, тоді

.

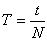У СІ [ Т ] = c.

Величину, обернену до періоду коливань Т, називають частотоюколивань n:

.

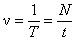Частота n показує скільки повних коливань здійснює коливальна система за одиницю часу. У СІ частоту вимірюють у герцах: частота дорівнює 1 Гц, якщо за 1 с коливальна система (маятник) виконує одне повне коливання: [ n ] = 1 Гц = 1/с = с^-1.

У теорії коливань часто користуються циклічною частотою (w) - величиною, яка показує скільки коливань здійснює маятник за 2p секунд. У СІ її вимірюють у герцах (Гц). Між частотою і циклічною частотою існує зв'язок:

.

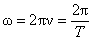У рівняннях (5.1.1) вираз в дужках під знаком синуса або косинуса називають фазоюколивань j = w t + j₀. Фаза коливань визначає при заданій амплітуді стан коливальної системи в довільний момент часу. У СІ цю величину вимірюють у радіанах (рад).

Якщо відлік часу в коливальній системі розпочати з моменту проходження тілом положення рівноваги, то коливання відбуваються за законом синуса, а якщо з точки максимального відхилення - то за законом косинуса.

У формулах (5.1.1) j₀ - початкова фаза - показує, на якому етапі знаходився коливальний рух у момент початку відліку часу.

Оскільки механічні коливання відбуваються під дією сил, то при цьому відбувається періодична зміна величини і напряму швидкості та прискорення тіла, що здійснює коливальний рух. Швидкість дорівнює першій похідній від зміщення х:

,

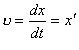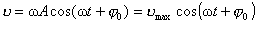, або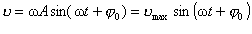

де _max = w A.

Прискорення дорівнює першій похідній від швидкості або другій похідній від зміщення

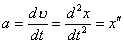
або

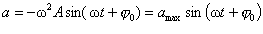, (5.1.2)

де a _max = – w² A.

Порівнюючи вирази (5.1.1) та (5.1.2) дістанемо диференціальне рівняння вільних гармонічних коливань.

Дата добавления: 2014-01-05