Математичне формулювання

Якісний опис

Нехай у певний момент часу на обкладинках конденсатора C існує певний заряд: додатній на одній із них, від'ємний на іншій. Оскільки обкладинки сполучені між собою колом, що складається з індуктивності і опору, то конденсатор почне розряджатися, а через коло потече струм. Збільшення струму на котушці індуктивності викликає в нійелектрорушійну силу, яка діятиме проти струму, перешкоджаючи йому зростати миттєво. Крім того, проходячи через активний опір, струм буде викликати нагрівання цього опору за законом Джоуля-Ленца, призводячи до втрат енергії.

Сила струму в колі буде збільшуватися доти, доки на обкладинках конденсатора залишатиметься заряд. Тоді, коли заряд на обкладинках конденсатора дорівнюватиме нулю, сила струму в колі буде максимальною, і відтоді почне зменшуватися. Зменшення струму в індуктивності призводить до виникнення електрорушійної сили, яка намагатиметься сповільнити це зменшення, тому струм в колі не зменшиться до нуля миттєво, а продовжуватиме протікати, заряджаючи конденсатор уже оберненим зарядом. На обкладинці, зарядженій спочатку додатньо, зосереджуватиметься від'ємний заряд, і навпаки. Максимального значення заряд досягне тоді, коли струм через коло спаде до нуля. В цю мить на обкладинках конденсатора утвориться заряд майже рівний початковому, тільки з оберненим знаком. Зменшення заряду зумовлене втратами в активному опорі, що викликають зменшення струму перезарядки. Далі процес повторюється в зворотньму напрямку - конденсатор починає розряджатися, викликаючи в колі струм, індуктивність спочатку обмежує швидкість зростання струму, а потім швидкість його зменшення викликає електрорушійну силу, що втримуе заряд, і, як наслідок, конденсатор знову заряджається.

Якщо втрати струму (на утворення тепла, на випромінювання електромагнітних хвиль, тощо) невеликі, то коливання можуть продовжуватися дуже довго. У ідеальному випадку нульвого опору - вічно. В реальних колах активний опір завжди існує, а тому реальні коливання завжди затухають.

Основним критерієм розгляду є умова постійності сили струму у всіх точках контура. Тобто сила струму в довільний момент часу повинна задовольняти всім законам притаманним постійному струму. Такий змінний струм називаєть квазістаціонарним. Диференціальне рівняння для класичного RLC-контура записується для невідомої динамічної змінної - електричного заряду і є математичним виразом закону Кірхгофа. Рівняння складається з трьох доданків - спадів напруги на індуктивності, на резисторі та напрузі на ємності, які в сумі повинні давати нуль:

,

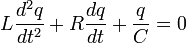Розв'язок цього рівняння має вигляд:

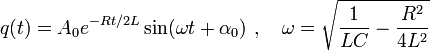
де 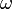- резонансна частота контура, - амплітуда коливань, 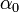- фаза. Таким чином, при замиканні перемикача в RLC-контурі виникають затухаючі коливання. Тому цей контур і називають коливальним контуром. Декремент затухання коливань у контурі визначається активним опором за формулою:

.

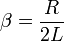Через цей коефіцієнт затухання можна виразити миттєву амплітуду коливань заряду конденсатора:

.

Різниця потенціалів 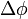на обкладинках конденсатора пропорційна заряду :

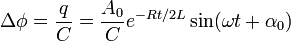
Залежність сили струму в коливальному контурі від часу має вигляд:

.

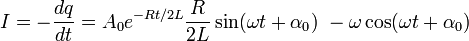Якщо в початковий момент часу заряд на обкладках конденсатора дорівнював , а струм в контурі був відсутній, то початкову фаза коливань 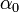та їхня амплітуда дорівнюють:

.

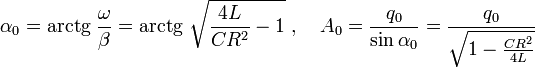Незатухаючі коливання

Якщо опір контура зменшувати до нуля 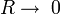, тоді в 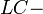контурі виникають незатухаючі коливання, для яких справедливі такі співвідношення:

.

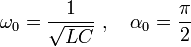Заряди, напруги та струми в коливальному контурі будуть у цьому випадку рівні:

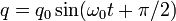
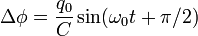
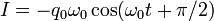
Період вільних незатухаючих коливань дорівнює

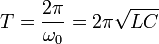(12)

Ця формула вперше була отримана в 1853 році В. Томсоном, тому і називається формулою Томсона.

Струм в контурі можна переписати у вигляді:

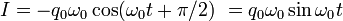. (13)

Тобто він відстає по фазі від різниці потенціалів на обкладках конденсатора на 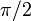. Амплітуда 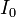сили струму, та амплітуда 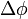різниці потенціалів дорівнюють:

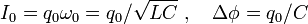(14b)

тому

,

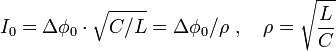де величину 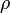називають хвилевим опором контура.

Дата добавления: 2014-01-05