Співвідношення невизначеностей як прояв корпускулярно-хвильового дуалізму властивостей матерії. Обмеженість механічного детермінізму

Розглянемо, наслідки що випливають з корпускулярно-хвильової двоїстості електронів, фотонів, протонів та інших об’єктів мікросвіту, і які обмеження накладає цей дуалізм на класичний метод описування їх руху і, зокрема, на можливість одночасного визначення їх імпульсів і координат.

У класичній механіці всяка частинка рухається певною траєкторією так, що фіксовані її координати та імпульс. Мікрочастинки внаслідок наявності в них хвильових властивостей відрізняються від класичних частинок. Одна з основних відмінностей полягає в тому, що мікрочастинка не має чіткої траєкторії, і неправомірно говорити одночасно про точні значення її координат та імпульсу.

Як відомо, будь-яка хвиля, незалежно від її природи, є процесом, що заповнює більшу чи меншу область простору, а через це не може локалізуватися в одній точці. Наприклад, уздовж осі ОХ рухається фотон, для якого точно відомий імпульс 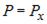, тобто 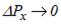. Такому фотону відповідає хвиля, довжина якої однозначно визначається величиною імпульсу .

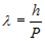Така монохроматична хвиля в просторі нічим не обмежена, область її існування – вся вісь ОХ. Це означає, що в цьому випадку просторовий інтервал 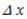, в якому замкнено об’єкт з хвильовими властивостями – фотон, дорівнює нескінченності. Іншими словами, при 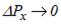маємо 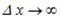. Отже, якщо точно відомий імпульс, локалізація фотона стає цілком невизначеною.

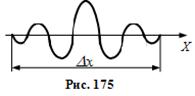
Якщо ж область локалізації фотона є обмеженою, то це означає, що амплітуда відповідного хвильового процесу відрізняється від нуля тільки всередині скінченного інтервалу 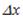і дорівнює нулю поза ним. Такий хвильовий процес уже не можна зобразити якою-небудь монохроматичною хвилею. Його можна уявити як суперпозицію ряду монохроматичних хвиль різної довжини. На рис. 175 наведено простий приклад суперпозиції трьох синусоїдальних хвиль, внаслідок чого відбувається хвильовий процес – так званий хвильовий пакет, амплітуда якого відрізняється від нуля в скінченному інтервалі .

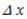Чим ширший інтервал 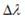можливих значень інтерферуючих хвиль (а разом з тим інтервал 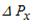можливих значень імпульсів), тим вужча область локалізації 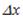результуючого пакета. Інакше кажучи, чим більша невизначеність імпульсу фотона, тим точніше можна визначити його координати. При 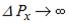маємо 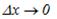, тобто точне значення координат фотона можливе тільки при повній невизначеності його імпульсу. Такі висновки справедливі не тільки для фотонів, а й для електронів, протонів та інших мікрочастинок.

У 1927 р. В. Гейзенберг, враховуючи хвильові властивості мікрочастинок, дійшов висновку, що об’єкт мікросвіту неможливо одночасно з однаковим ступенем точності характеризувати і координатами, й імпульсом. Згідно з співвідношенням невизначеностей Гейзенберга мікрочастинка не може одночасно мати і певну координату 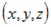і певну відповідну проекцію імпульс 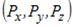, причому невизначеності в значеннях цих всіх величин задовольняють умови

, , ,

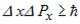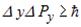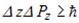тобто добуток невизначеностей координати і відповідної їй проекції імпульсу не може бути меншим від величини .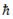

Неможливість одночасно точно визначити координату і відповідну складову імпульсу не пов’язана з недосконалістю методів вимірювання та вимірювальних приладів, а є наслідком подвійної корпускулярно-хвильової природи мікрооб’єктів. Співвідношення невизначеностей отримано при одночасному використанні класичних характеристик руху частинки (координати, імпульсу) і наявності у неї хвильових властивостей.

Оскільки в класичній механіці приймається, що вимірювання координати та імпульсу може бути проведено з будь-якою точністю, то, таким чином, співвідношення невизначеностей є квантовим обмеженням застосовності класичної механіки до мікрооб’єктів.

4. Подання стану частинки в квантовій механіці.

В класичній механіці при одномірному русі вздовж осі х стан частинки в кожний момент часу t задається двома величинами: координатою частинки x(t) і її швидкістю 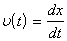або імпульсом частинки 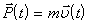. Таке визначення стану частинки є головним вихідним моментом побудови класичної механіки.
В фізиці мікрочастинок з наявністю у них хвильових властивостей, класичне визначення стану частинки втрачає будь-який зміст, а з ним і поняття сили, яка за визначенням є функцією класичного стану.
Встановити фізичний зміст квантового стану допомогло відкриття корпускулярно-хвильового дуалізму матерії. В квантовій фізиці стан частинки задається хвильовою функцією, яка є комплексною величиною і визначається у всіх точках простору і в будь-який момент часу.
Аналогічно класичним хвилям рух елементарних частинок характеризується хвилями де Бройля.
Рівняння хвилі де Бройля елементарної частини називається хвильовою функцією і позначається 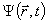. Хвильова функція Y(r,t) не має жодного відношення до механічних хвиль. Класичні хвилі поширюються в пружних середовищах, а елементарні частинки можуть рухатись також і у вакуумі. Слід мати на увазі, що хвилі де Бройля властиві будь-яким частинкам, як зарядженим так і нейтральним, в той час як електромагнітні хвилі випромінюються лише зарядженими частинками при їх прискореному русі.
Для класичних хвиль характерні найбільш суттєві властивості, такі як енергія, імпульс, інтенсивність, яка визначається квадратом амплітуди хвилі.
Поняття фізичного змісту хвильової функції прийшло після того, як вияснилось, що в інтерференції хвиль де Бройля проявляються властивості окремих частинок, а не їх системи. Це підтверджується незалежністю інтерференції від інтенсивності частинок в пучку. Інтерференція спостерігається навіть в тих випадках, коли за час польоту від джерела до детектора пролітає лише одна частинка. Цей факт можна тлумачити так лише у випадках, коли рух будь-якої мікрочастинки підпорядковується статистичним закономірностям.
За аналогією з класичними хвилями знайдемо фізичний зміст квадрата модуля хвильової функції

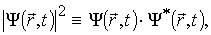, (1.19)
де 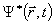-функція, комплексно спряжена до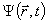
В досліді Девісона і Джермера, схема якого показана на рис.1.1 встановлено, що струм, який реєструється гальванометром, пропорційний квадрату модуля хвильової функції
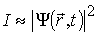. (1.20)
З іншого боку величина цього струму пропорційна також об’єму детектора dV
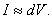. (1.21)
З урахуванням (1.20) і (1.21) маємо:
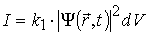. (1.22)
Якщо імовірність попадання частинок в детектор дорівнює dp, то величина струму гальванометра буде також пропорційною величині цієї імовірності
I = k₂dp. (1.23)
Прирівнявши рівності (1.22) і (1.23), одержимо:
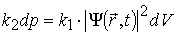. (1.24)

Завжди можна вибрати значення хвильової функції такою, щоб k₁=k_2. Тоді (1.24) набуде вигляду
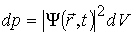. (1.25)
Звідки
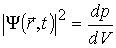. (1.26)
Квадрат модуля хвильової функції (1.26) визначає густину імовірності виявити частинку в точці з радіусом-вектором 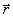в момент часу t. Квантова механіка на відміну від класичної дає імовірнісне пояснення квантового стану, а хвильова функція має статичний зміст.
При відомій хвильовій функції рівність (1.26) дозволяє визначити імовірність виявити частинку в об’ємі dV
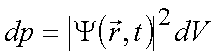. (1.27)
Якщо частинка знаходиться в довільній точці простору, то ця подія є достовірною, а імовірність такої події дорівнює одиниці, тобто
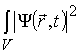dV =1. (1.28)
Умова (1.28) називається умовою нормування.
Як бачимо, квантова механіка має статистичний характер; у ній не ставиться питання про знаходження положення частинки або її траєкторії в просторі, так як завдяки хвильових властивостей мікрочастинок такі питання взагалі втрачають зміст. В квантовій механіці за допомогою хвильової функції 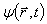визначається лише імовірність виявлення мікрочастинки в різних точках простору. З сказаного випливає, що хвильова функція 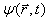повинна задовольняти певним обмежувальним умовам, які ще називаються стандартними умовами: воно має бути скінченою, однозначною і неперервною, так як імовірність не може бути більшою за 1; бути неоднозначною і змінюватись стрибкоподібно.

Дата добавления: 2014-01-05