Та контролю знань

Щодо закріплення знань і навиків розв’язання практичних задач при здійсненні статистичних групувань і побудові атрибутивних і варіаційних рядів пропонується виконати лабораторну роботу під час лабораторних занять, а також під час практичних занять і самостійно розв’язати декілька задач, аналогічних наведеним у цьому параграфі.

Таблиця 3

Термін (поняття)	Визначення (формула)
§ 3.1. Зміст статистичного узагальнення(► рис.1.2)
1. Узагальнення статистичних даних (СУ)	Другий етап процесу статистичного дослідження соціально-економічних явищ (процесів), метою якого є опрацювання даних первинного обліку (результатів СС) шляхом їх систематизації в певній формі відповідно до спеціальної програми СУ (► п.3.2) і, як правило, з подальшим поданням результатів опрацювання у відповідних звітно-статистичних документах (статистичних звітах) (► п.3.19). Основа СУ – метод статистичних групувань (► п.1.9).
§ 3.2. Програма статистичного узагальнення
2. Програма статистичного узагальнення	Документ (організаційний план), що регламентує способи, правила та порядок систематизації первинних даних, переважно, в системі макетів розроблюваних таблиць; є логічним продовженням програми СС.
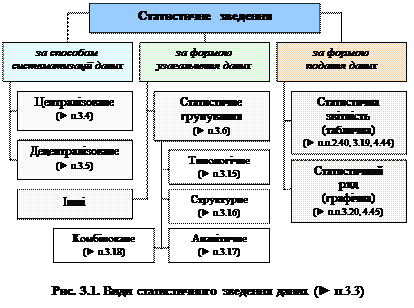
3. Статистичне зведення (► рис.3.1)	Систематизація первинної статистичної інформації, що відбувається в певній формі й дозволяє перейти до узагальнюючих показників, які характеризують досліджувану сукупність у цілому й її окремі частини. Задачами зведення є: 1) утворення соціально-економічних типів явищ; 2) вивчення структури явищ й їх структурних зрушень; 3) виявлення зв’язків між досліджуваними ознаками. Відбувається в два способи: централізований (► п.3.4) і децентралізований (► п.3.5). Кінцевою метою зведення є система макетів розроблюваних таблиць (► п.4.44), в яких містяться систематизовані дані.
4. Централізоване зведення	Спосіб статистичного зведення, що передбачає зосередження усіх даних в одному місці за розробленою методикою.
5. Децентралізоване зведення	Спосіб статистичного зведення, що передбачає систематизацію даних знизу доверху за ієрархічною системою управління, в якій дані опрацьовуються на кожному етапі їх передачі (управління).
6. Статистичне групування	Одна з основних форм статистичного зведення, що має на меті утворення однорідних груп шляхом поділу статистичної сукупності на однорідні частини або об’єднання досліджуваних одиниць в окремі сукупності за суттєвими для них групувальними ознаками (► п.3.7).

Продовження таблиці 3

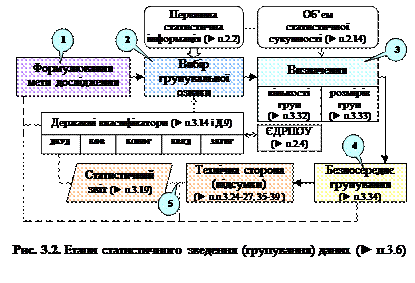
6. Статистичне групування (продовження)	Групування поділяють на: типологічні (► п.3.15), структурні (► п.3.16), аналітичні (► п.3.17), комбіновані (► п.3.18). Особливим видом групувань є класифікація (► п.3.14). Етапами групування є (► рис.3.2): 1) формування задачі зведення даних; 2) визначення групувальної ознаки, кількості груп, їх розмірів, безпосереднє формування груп і підгруп; 3) технічна сторона зведення (перевірка повноти і якості даних, підведення підсумків, розрахунки окремих показників тощо). Групування мають відповідати наступним вимогам: 1) утворювані групи мають бути однорідними (якісно і кількісно); 2) не можна поєднувати в одну і ту ж саму групу одиниці, що відносяться до інших сукупностей; 3) має бути забезпеченою оптимальна наповнюваність одиницями сукупності в групах; 4) групувальна ознака має відповідати меті дослідження.
7. Групувальна ознака (ГО)	Статистична ознака, покладена в основу групування. Групувальні ознаки класифікуються аналогічно (► п.п.1.2, 3.8-13).
8. Атрибутивна ГО	Ознака, що має лише змістовне (якісне) вираження. Приклади: стать людини (чоловіча і жіноча), спеціалізація магазинів (продовольчі та непродовольчі), форма власності (державна, колективна, приватна) і т.д.
9. Варіаційна (кількісна) ГО	Ознака, що має числове (кількісне) вираження. Приклади: об’єм товарообороту, прибуток, трудовий стаж, розмір заробітної плати, чисельність працівників тощо.
10. Альтернативна ГО	Ознака, що набуває одного з двох протилежних за змістом значень. Приклади: стать людини (чоловіча і жіноча), час доби (день і ніч), боки медалі (аверс і реверс), рівні цифрового сигналу (нуль і одиниця), якість продукції (стандартна і бракована) тощо.
11. Множинна ГО	Ознака, що набуває множини значень, тобто окремі одиниці досліджуваного явища можуть мати різні значення (варіанти). Приклади: організаційно-правові форми, види економічної діяльності, трудовий стаж, кількість членів сім’ї, рівень доходів тощо.
12. Факторна ГО	Причинна ознака, що обумовлює зміну іншої, результативної, ознаки. Приклади: трудовий стаж або рівень кваліфікації працівника (факторні ознаки) зумовлюють його заробітну плату (результативна ознака); заробітна плата (факторна ознака), у свою чергу, зумовлює рівень споживання (ціну, кількість, вартість, якість) людиною товарів і послуг (результативна ознака) тощо.

Продовження таблиці 3

13. Результативна ГО	Наслідкова ознака, зміна якої зумовлена впливом іншої, факторної, ознаки. Приклади див. в п.12 цієї таблиці.
14. Класифікація (класифікатор)	Стала номенклатура класів і груп, що утворені на основі схожості та відмінностей одиниць спостереження; виступає в ролі своєрідного статистичного стандарту. Приклади: класифікація виробленої продукції, товарів народного споживання, що враховуються в роздрібному товарообороті, у витратах обігу; класифікації по труду – по професіях, по заняттях тощо. Серед державних розповсюдженими є такі класифікатори: Державний класифікатор управлінської документації (ДКУД), класифікатор організаційно-правових форм (КОПФ), класифікатор форм власності (КФВ), класифікатор видів економічної діяльності (КВЕД), загальний класифікатор галузей народного господарства (ЗКГНГ), система позначень об’єктів державного управління (СПОДУ), класифікатор об’єктів адміністративно-територіального устрою України (КОАТУУ) (► Д.9).
§ 3.3. Види статистичних групувань(► рис.3.1)
15. Типологічне групування	Групування, що утворює в якісно різнорідній сукупності даних однорідні групи явищ за основною (типовою) ознакою. Основною ознакою є суттєва ознака, що визначає головний зміст досліджуваного явища. Приклади: групування населення за статево-віковою ознакою, підприємств – за формою власності і т.д. (► з.№2).
16. Структурне групування	Групування, метою якого є вивчення структури досліджуваної сукупності шляхом поділу якісно однорідної сукупності на групи за певною варіаційною ознакою. Приклади: вивчення складу товарообороту по товарних групах, поділ торгівельної мережі за спеціалізацією, розподіл працівників по професіях, за віком, трудовим стажем, освітою тощо (► з.№№3-5).
17. Аналітичне групування	Групування, метою якого є вивчення причинно-наслідкових зв’язків між ознаками, що характеризують досліджуване явище в якісно однорідній сукупності даних, причому факторні і результативні ознаки можуть бути і атрибутивними, і варіаційними. Приклади (► п.3.12 і з.№6).
18. Комбіноване групування	Групування, що утворює однорідні групи за двома і більше ознаками, взятими в певному сполученні, у послідовності, виходячи з логіки взаємозв’язків цих ознак. Приклади: розподіл підприємств за формою господарювання, по підгрупах за рівнем рентабельності, продуктивності праці, фондоємності тощо (► з.№7).

Продовження таблиці 3

§ 3.4. Форми подання зведених даних. Статистична звітність
19. Форми систематизації даних	Це, перш за все, статистичні звіти, основу яких складають статистичні таблиці (таблична форма) (► п.4.44). Крім того, поширеною формою є статистичні графіки (графічна форма) (► п.4.45), які, разом зі статистичними таблицями, уможливлюють представлення результатів зведення (групування) у виді статистичних рядів. Види статистичних звітів: а) за призначенням: б) за змістом: - загальнодержавні; - типові; - відомчі (галузеві); - спеціалізовані; в) за часом реєстрації даних: г) за способом подання: - поточні (місячні, квартальні); - термінові; - річні; - поштові.
§ 3.5. Статистичні ряди(► рис.3.2)
20. Статистичний ряд розподілу	Упорядковане представлення (розташування) одиниць досліджуваної сукупності в групах за групувальною ознакою.
21. Варіаційний ряд	Статистичний ряд, утворений за кількісною ознакою, як залежність числової характеристики чисельності цієї ознаки від її значень у статистичному ряду.
Дискретний варіаційний ряд
22. Дискретний варіаційний ряд (ДР)	Статистичний ряд, оснований на перервній варіації ознаки, котрий встановлює залежність між абсолютною (відносною) частотою дискретної ознаки й її фактичними значеннями в ряду (варіантами) (► п.3.28/рис.).
23. Варіант (хj)	Окреме значення ознаки, якого вона набуває у статистичному ряду (j = 1,…, m).
24. Абсолютна частота дискретної ознаки (fj)	Кількість одиниць статистичної сукупності з одним і тим самим значенням ознаки (або чисельність окремого варіанта в дискретному ряду) (j = 1,…, m).
25. Об’єм ДР (N)	Сума абсолютних частот дискретного ряду:

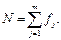
Продовження таблиці 3

26. Відносна частота (частість) дискретної ознаки (ω_j)

Відношення абсолютної частоти дискретної ознаки до об’єму ряду (нормування):  

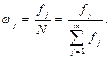
27. Умови нормування в ДР

Сума відносних частот (частостей) дискретного ряду завжди дорівнює одиниці (ста відсоткам):  

28. Многокутник розподілу

Графічне зображення (лінійна діаграма) дискретного варіаційного ряду (► п.3.22). Інша назва – полігон частот.

f ₃(ω ₃)

f_N (ω_N)

f_{N -1}(ω_{N -1})

f ₂(ω ₂)

f ₁(ω ₁)

Рис. Много-

кутник

розподілу.

Інтервальний варіаційний ряд

29. Інтервальний варіаційний ряд (ІР)

Статистичний ряд, оснований на неперервній зміні ознаки, котрий встановлює залежність між щільністю (► п.3.40/рис.1 і рис.2) (крім того, абсолютною (відносною) частотою в рівномірному інтервальному ряду (рис.1)) інтервальної ознаки й її значеннями на границях інтервалів.

30. Рівномірний ІР

Інтервальний ряд з однаковими за довжиною інтервалами (► п.3.40/рис.1).

31. Нерівномірний ІР

Інтервальний ряд з неоднаковими за довжиною інтервалами (► п.3.40/рис.2).

32. Кількість інтервалів в рівномірному ряду (n)

Визначається за формулою Стерджесса: n = 1 + 3,322 ∙ lg N,   де N – об’єм інтервального ряду.

Продовження таблиці 3

33. Довжина інтервалу в ІР (∆ j)	∆ j = x в j – x н j ,   де x в j і x н j – верхня і нижня границі j -го інтервалу. В рівномірному інтервальному ряду вона визначається так:   ∆ = (x max – x min) /n, –   де x max і x min – максимальне і мінімальне значення ознаки.
34. Правило групування в ІР	В j -ий інтервал потрапляють тільки ті значення ознаки, що є не меншими, ніж його нижня границя (є «закритою», або «включно»), і менші за його верхню границю (є «відкритою», або «виключно»), крім останнього j -го інтервалу, обидві границі якого є «закритими»; нижня границя першого інтервалу і верхня границя останнього інтервалу співпадають з мінімальним і максимальним значеннями ознаки відповідно; нижня границя кожного наступного інтервалу співпадає з верхньою границею попереднього інтервалу:   x н j ≤ xij < x в j (j = 1, …, n – 1), x н n ≤ xin ≤ x в n ; x н1 = x min, x в n = x max; x в j = x н j + Δ j, x н j = x в j -1.   Іноді, під час аналітичних групувань, результативна ознака може бути представленою інтервально, так, що і верхня, і нижня границі всіх інтервалів визначаються «закритими».
35. Абсолютна частота інтервальної ознаки (fj)	Кількість значень ознаки в межах j -го інтервалу.
36. Об’єм ІР (N)	Сума абсолютних частот інтервального ряду:
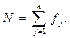
37. Відносна частота (частість) інтервальної ознаки (ωj)	Відношення абсолютної частоти інтервальної ознаки до об’єму інтервального ряду (нормування):

Продовження таблиці 3

38. Умови нормування в ІР

Сума відносних частот (частостей) інтервального ряду завжди дорівнює одиниці (ста відсоткам):  

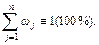
39. Щільність інтервальної ознаки (φ_j)

Співвідношення частості інтервальної ознаки j -го інтервалу і довжини цього інтервалу:   φ_j = ω_j / ∆ _j.

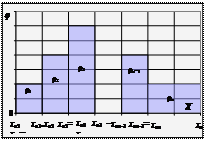
40. Гістограма    

Графічне зображення (стовпчикова діаграма) інтервального варіаційного ряду. ←Рис. 1. Гістограма рівномірного інтер- вального ряду

…

ряду.

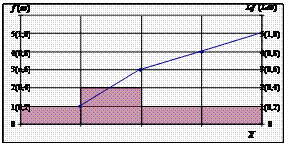
41. Кумулята (∑ f або ∑ ω)   Рис. Кумулята

Накопичена частота (частість) ознаки; уворюється як сума частот (частостей) окремих варіантів (інтервалів) статистичного ряду із зростанням значень ознаки: Графічно – це зростаюча від 0 до N ламана лінія з точками перегину, що відповідають рівностям:

 

3.4. Питання для підготовки до занять, самоаналізу

1. Узагальнення статистичних даних: сутність, місце у структурно-логічній схемі процесу статистичного дослідження, використовуваний метод статистики.

2. Програма статистичного узагальнення: визначення, програмно-методичні й організаційні питання, форми укладання.

3. Поняття статистичного зведення, способи зведення даних.

4. Поняття статистичного групування, групувальної ознаки та класифікації; види класифікаторів.

5. Види групувальних ознак, їх сутність.

6. Види статистичних групувань, їх сутність.

7. Задачі й етапи зведення та групування даних, вимоги до статистичних групувань.

8. Форми систематизації даних, поняття статистичного ряду.

9. Види статистичних рядів, основні елементи ряду, способи подання.

10. Дискретний варіаційний ряд: визначення, елементи ряду (варіант, абсолютна частота, частість), основні форми подання, способи та правила побудови.

11. Інтервальні варіаційні ряди: визначення, види, елементи ряду (границі інтервалів, абсолютна інтервальна частота, частість, щільність ознаки в інтервалі), основні форми подання, способи та правила побудови.

12. Кумулята: визначення, елементи (накопичена частота, накопичена частість), основні форми подання, способи та правила побудови.

13. Правила побудови рівномірного інтервального ряду по даних дискретної статистичної ознаки.

Дата добавления: 2014-01-05