
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для нотаток
|
|
|
|
Щодо закріплення знань і навиків розв’язання практичних задач з оцінки параметрів і перевірки статистичних гіпотез пропонується виконати лабораторну роботу під час лабораторних занять, а також під час практичних занять і самостійно розв’язати декілька задач, аналогічних наведеним у цьому параграфі.
4.3. Статистичні таблиці та графіки
Формалізовано статистична інформація подається, в першу чергу, у статистичних таблицях (► п.4.44 і рис.4.3) і статистичних графіках (► п.4.45 і рис.4.4), а, по-друге, існує аналітична форма представлення статистичної інформації, як результат математичних дій з первинними даними під час статистичного аналізу.
Статистичні таблиці (надалі – таблиці) складають основу звітно-статистичної документації (► п.2.7) і є головним елементом статистичних звітів (► п.п.2.40 і 3.19).
Термін «таблиця» має латинське походження: «tabula» – дошка [36, 37].
Таблична форма відображення інформації полягає в такій організації структури даних, в якій окремі елементи розташовані в комірках (клітинках), кожній з яких відповідає пара значень – номер рядка і номер графи (стовпчика). Таким чином встановлюється змістовний зв’язок між елементами таблиці: підметом і присудком.
Будуючи таблиці, треба дотримуватись таких правил.
1. Таблиця будується невеликого розміру, легко доступною для огляду; краще замість однієї складної таблиці великого розміру побудувати декілька логічно пов’язаних між собою таблиць меншого розміру.
2. Таблиця супроводжується заголовком, в якому відображається час, територія, одиниці вимірювання ознаки або показника (якщо вона єдина для всього присудка; в протилежному випадку кожна графа міститиме у своєму заголовку відповідну одиницю вимірювання).
3. Скорочення в таблицях забороняються, крім загальноприйнятих.
4. Підмет і присудок мають бути об’єктивно пов’язаними між собою, а присудок повинен давати повну характеристику кожної групи підмета відповідно до мети дослідження.
5. Звичайно по графах і рядках таблиці підводиться підсумок (там, де він є доцільним). Якщо певна кількість одиниць представлена складовими по окремих групах, останні подаються в таблиці після фрази «в тому числі» (скорочено – «в т.ч.»).
6. Графи підмета звичайно позначаються буквами (А, Б, В, …), а графи присудка – арабськими цифрами (1, 2, 3, …). Нумерація рядків, якщо вона є доцільною, наскрізна та виконується арабськими цифрами, починаючи з 1, першого найменування в підметі.
7. У клітинках таблиці допускається застосування наступних символів:
- «-» – прочерк – означає відсутність явища;
- «…» – три крапки – відсутність інформації або «немає відомостей»;
- «×» – перехрестя – інформація відповідно запису присудка є нелогічною.
8. Дані однієї й той же самої графи повинні подаватися з однаковим ступенем точності (однаковою кількістю цифр після коми), для чого застосовуються правила округлення чисел; відсутні розряди заповнюються нулями, наприклад, число 1,5 із ступенем точності 0,01 записується як «1,50». У багатозначних числах класи зручно виділяти пробілами, наприклад, число 1000000 записується як «1 000 000». Іноді такі числа записуються із застосуванням умовних скорочень, наприклад: «1 млн.» або «1 × 106», – а якщо всі дані цієї графи одного порядку, умовне скорочення, в даному випадку «млн.» або «× 106», виноситься в заголовок присудка.
9. Якщо звітні дані супроводжуються додатковими математичними обрахунками, пояснення до останніх робляться в довідці внизу під таблицею, рідше – в заголовку присудка.
10. Аналіз таблиці краще виконувати, починаючи з підсумку, який характеризує сукупність у цілому, переходячи потім до характеристики складових за їх значущістю (важливістю) в підсумку.
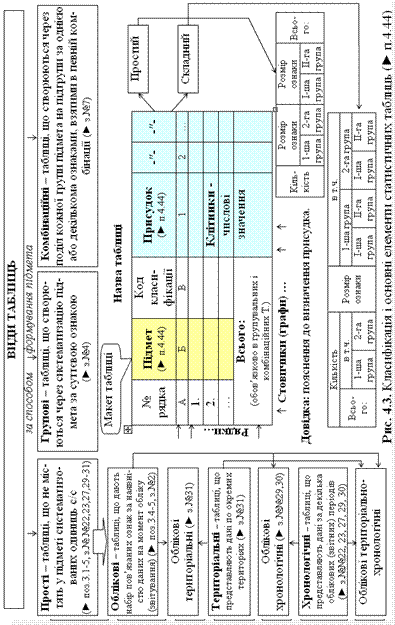
Статистичний графік (надалі – графік) – це наочна, виразно сприймана форма відображення статистичної інформації, яка передбачає використання в якості основних зображувальних засобів ліній, штрихів, точок, є логічним продовженням і доповненням до табличної форми й, поряд з цим, має важливе аналітичне значення.
Термін «графік» має грецьке походження: «γραφω» – пишу, креслю, малюю[18].
Порівнянність показників, тенденції розвитку досліджуваної ознаки у часі (просторі) або взаємозв’язку ознак між собою, приховані за великим обсягом інформації у таблицях, на графіках відразу можна побачити явно. На відміну від таблиці, графік завжди потребує впорядкованості даних – прив’язки до шкали, де числові дані розташовані в порядку збільшення їх значень.
Засновником графічного методу у статистиці вважають шотландського інженера і політичного економіста Вільяма Плейфейра (1759-1823), в «Комерційному і політичному атласі» якого вперше (1786) статистичні дані були зображені на лінійних, стовпчикових, секторних й ін. діаграмах.
Будуючи графіки треба дотримуватись таких правил.
1. Сторони поля графіка звичайно пов’язані пропорцією «золотого перерізу», як сторони прямокутника з відношенням сторін від 1: 1,3 до 1: 1,5, рідше – як сторони квадрату.
2. Графік має найбільш дохідливо відображати досліджувані показники та відповідати меті дослідження. Дохідливість зображення залежить від правильно й оптимально вибраного масштабу.
3. Відображаючи на графіку дані, необхідно суворо дотримуватись встановленого масштабу.
4. Універсальним графіком є діаграма – графік, на якому статистична інформація відображається за допомогою геометричних фігур або символічних знаків (► з.№№2-10, 14, 22-29, 31, 32). Діаграми є більш наочним та дохідливим, ніж картограми [19], тому їх поєднання з географічною картою дає картодіаграму.
5. Для побудови лінійних діаграм звичайно застосовується прямокутна[20] система координат, в якій початок відліку даних починається від 0 – початку координат, а осями є вісь абсцис і вісь ординат (в двомірній системі).
6. Для раціонального використання поля графіка допускається умовне перенесення початку координат в певну точку масштабної шкали, наприклад: в найближчу зліва від мінімального значення змінної (► з.№№3-7, 9) або в центр області визначення незалежної змінної (► п.7.16 і з.№№22, 23).
7. По осі абсцис завжди відлічуються значення незалежної змінної, а по осі ординат – залежної змінної: відповідно зліва на право і від низу до верху. Масштабні орієнтири впродовж осі абсцис розташовуються під віссю, а впродовж осі ординат – зліва від осі, так, що б відповідні числа і точки масштабної шкали знаходились напроти одне одної.
8. Контрольні точки лінійної діаграми в площині графіка з’єднуються прямими лініями, якщо така діаграма характеризує емпіричні дані (► з.№4), і плавною лінією, якщо вона представляє теоретичну функціональну залежність (► з.№8).
9. На одному й тому ж самому полі графіка можна зображати декілька показників з метою порівняння специфіки їх розвитку, наприклад, у часі (► з.№№22-28) або характеру зміни певного показника, властивого різним просторовим (територіальним) об’єктам (► з.№31).
10. При побудові стрічкових (► з.№№2, 29) і стовпчикових (► з.№10) діаграм повинно дотримуватись таких правил: ширина стрічок (стовпчиків) має бути однаковою, а відлік на масштабній шкалі починається з нульової відмітки.
11. Площина кола кругової діаграми (► з.№14) обирається за 100% об’єму досліджуваної статистичної сукупності, а площина кожного сектора – це частість (%) окремої частини (групи) сукупності.
12. Символи фігурних діаграм (► з.№31) мають відповідати змісту зображених понять; вони є найбільш виразними та зорове легко сприймаються.
13. Порівнянність шуканих показників через застосування знаків Варзара (► з.№29) досягається визначенням площини кожного знака-прямокутника, яка повинна дорівнювати добутку довжини його сторін: основи і висоти.
14. Заголовок (титул) графіка повинен бути стислим, чітко пояснюючи зміст останнього.
15. Числові дані, по яких будується графік, звичайно доповнюють його зображення, розташовуючись в окремій таблиці, яка, так само, як і графік, відбиває залежність між змінними.
Таблиці та графіки стали невід’ємною складовою опрацювання статистичних даних. Їх побудова сьогодні спрощується завдяки розробленню прикладних комп’ютерних програм.

Рис. 4.1. Методологія статистичного аналізу
 Форми
Етапи
дослідження Форми
Етапи
дослідження
| Таблична | Графічна | Аналітична | |||||
| І. Статистичне спостереження (► гл.2) | Статистичні таблиці (► п.4.44 і рис.4.3): | Статистичні формуляри (► п.2.53) | х | х | ||||
| ІІ. Статистичне узагальнення (► гл.3) |   Статистичні
звіти
Статистичні
звіти
 (► п.п.2.40 і 3.19) (► п.п.2.40 і 3.19)
| Діаграми, картограми, картодіаграми (► п.4.45 і рис.4.4) | х | |||||
| Емпіричні функції розподілу (варіаційні ряди): многокутник розподілу (► п.3.28), гістограма (► п.4.40), кумулята (► п.4.41) |  + теоретичні розподіли теорії ймовірностей (► п.п.4.12-19) + теоретичні розподіли теорії ймовірностей (► п.п.4.12-19)
| |||||||
| ІІІ. Статистичний аналіз (► гл.4) | Розрахункові таблиці-матриці | Система статистичних показників (► гл.5), в т.ч. числові характеристики закономірності (► § 4.2) | ||||||
| Вибірковий метод (► гл.6) | Довірчий
  інтервал
(► п.6.22) інтервал
(► п.6.22)
| + вибіркові розподіли
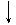
|  Вибіркові оцінки (► п.п.4.24 і 6.10): Вибіркові оцінки (► п.п.4.24 і 6.10):
| параметрів ГСС (► п.6.9) | + функціонали (квантилі, ► п.4.8) | |||
| Метод рядів динаміки (► гл.7) | Діаграма ряду динаміки; модель сезонної хвилі | + лінія тренду | параметрів моделі тренду | Показники динаміки (► § 7.2) | ||||
| КРАЗ (► гл.9) | Кореляційне поле | + лінія регресії | параметрів моделі регресії | Показники зв’язку (►§§9.2, 3) | ||||
| Індексний метод (► гл.8) | х | Статистичні індекси (► § 8.2) |
Рис. 4.2. Форми подання статистичної інформації (► п.3.19)
 |
 |
Таблиця 4
| Термін (поняття) | Визначення (формула) |
| § 4.1. Зміст статистичного аналізу(► рис.4.1) | |
| 1. Статистичний аналіз (СА) | Третій етап процесу статистичного дослідження соціально-економічних явищ (процесів), метою якого є виявлення властивих їм закономірностей (► п.4.5) на основі системи узагальнюючих статистичних показників (► п.4.2) відповідно до методів статистичного аналізу (► п.4.3). Основа СА – метод узагальнюючих статистичних показників (► п.1.9). Обраний метод статистичного аналізу (► п.1.9) та відповідні статистичні показники (► п.1.3) мають бути адекватними задачі дослідження (► п.1.11). |
| 2. Система узагальнюючих статистичних показників | Основа статистичного аналізу (► рис.1.2); сукупність статистичних показників, обчислюваних по всіх одиницях досліджуваної сукупності або її окремої частини, таких, що представляють у цієї сукупності шукані закономірності у виді числових характеристик (чисел). Їх основу складають середні величини (► §5.3) і показники варіації (► §5.4), за допомогою яких обчислюються числові характеристики закономірностей статистичних розподілів (положення (► п.4.9), розсіювання (► п.4.10), асиметрії й ексцесу (► п.4.11) й ін.), показники динаміки (► §7.2), індекси (► §8.2), показники зв’язку (► §§9.2, 3). |
| 3. Метод (задачі) СА | Комплекс методів, способів, прийомів, операцій, правил, необхідних для досягнення мети аналізу, розв’язання конкретної задачі або певної задачі з конкретного класу задач. Основним класам задач статистичного аналізу відповідають певні методи статистики (► п.1.9): 1) вивчення структури об’єкта дослідження відбувається за допомогою методів статистичних групувань, узагальнюючих статистичних показників; 2) оцінка просторових, часових змін ознаки, а також впливу факторів, що їх зумовлюють, здійснюється за допомогою методу рядів динаміки (► гл.7) й індексного методу (► гл.8); 3) виявлення й оцінка причинно-наслідкових (факторних) зв’язків між ознаками проводяться за допомогою КРАЗ (► гл.9). В основу цих методів покладений принцип несуцільного вибіркового статистичного дослідження (► гл.6). |
Продовження таблиці 4
| 3. Метод (задачі) СА (продовження) | Дві головні задачі методу – оцінка параметра (► п.4.24) і перевірка статистичної гіпотези (► п.4.31). До поширених конкретних задач статистичного аналізу відносять: аналітичне вирівнювання у статистичних рядах (► п.4.29); пошук основної тенденції розвитку (тренду, регресії) (► §§7.3, 9.2), прогнозування (►§§7.4, 9.6) та вивчення сезонних коливань в рядах динаміки (► §7.5); індексація статистичних сукупностей (► §8.1). У комплексі, крім того, застосовуються такі поширені методи: максимальної правдоподібності (► п.6.15) та найменших квадратів (► п.п.7.16, 9.12), апроксимації (► п.7.16) й екстраполяції (► п.7.23) (у вибіркових дослідженнях, рядах динаміки, КРАЗ), збільшення інтервалів (► п.7.28) і плинного середнього (► п.7.29) (в рядах динаміки щодо виявлення тренду) й ін. До поширених способів відносять наступні: відліку часу від умовного початку (► п.7.16) (у рядах динаміки щодо визначення параметрів моделі тренду), постійного (змінного) середнього (► п.7.31) (в рядах динаміки щодо побудови моделі сезонної хвилі), визначників (щодо визначення параметрів моделей тренду в рядах динаміки (► п.7.16) й регресійних моделей в КРАЗ (► п.9.12)) й ін. |
| § 4.2. Статистичний закон і закономірність | |
| 4. Закон розподілу ймовірностей випадкової величини | Співвідношення, що встановлює залежність між імовірністю випадкової величини X і значеннями цієї випадкової величини х, найчастіше: у значеннях її ймовірностей[21] p(x) = P{ X = x }, функції F(x) = P{ X < x }[22] або щільності f(x) = dF / d x [23] розподілу її ймовірностей (остання характеристика справедлива для неперервних величин). Закони розподілу випадкових величин застосовують як імовірнісні моделі у статистичному аналізі досліджуваних ознак (статистик), характеризуючи залежність між числовою характеристикою чисельності статистичної ознаки X (статистики) і значеннями цієї ознаки х (статистики) у статистичних рядах (розподілах) (► п.3.20). |
Продовження таблиці 4
| 5. Закономірність розподілу | Властивість розподілу, що має прояв у його узагальнюючих числових характеристиках (моментах): квантилях (статистиках, ► п.4.8), характеристиках положення (середніх величинах, ► п.4.9), характеристиках розсіювання (показниках варіації, ► п.4.10), характеристиках асиметрії й ексцесу (► п.4.11). |
| 6. Початковий момент порядку r (M r (Х) або M r) | Числова характеристики закономірності розподілу ймовірностей дискретної та неперервної випадкових величин (положення), яка дорівнює відповідно:
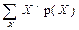 і і 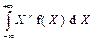 .
У статистичних рядах p (X) набуває змісту частості ω. .
У статистичних рядах p (X) набуває змісту частості ω.
|
7. Центральний момент порядку r (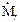 (Х) або (Х) або 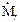 ) )
| Числова характеристики закономірності розподілу ймовірностей дискретної та неперервної випадкових величин (розсіювання), яка дорівнює відповідно:
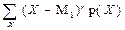 і і 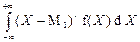 .
У статистичних рядах p(X) набуває змісту частості ω. .
У статистичних рядах p(X) набуває змісту частості ω.
|
8. Квантиль (xq) порядку q
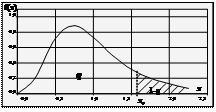 (статистика) (статистика)
| Таке значення xq випадкової величини (ознаки) Х, для якого існує ймовірність q = Р{ X < xq } = F(xq) (0 < q < 1). У розподілах розрізняють такі квантилі: х 1/2 – медіану; х 1/4 , х 2/4 , х 3/4 – квартилі; х 1/10, х 2/10, …, х 1/10, х 2/10, х 9/10 – децилі; х 1/100, х 2/100, …, х 99/100 – процентилі. процентилі. Рис. Квантиль xq розподілу f(x). |
| 9. Характеристики положення (середні величини) | 1) Центр розподілу (математичне сподівання) M(X) = m Х. 2) Медіана Me = х 1/2. 3) Мода (Mo): найчисельніше (найімовірніше) значення Х (розподіл з однією, двома і більше модами називають відповідно одно-, двох- і багатомодальним). |
Продовження таблиці 4
| 10. Характеристики розсіювання (показники варіації) | 1) Розмах варіації (R) – різниця між найбільшим x max і найменшим x min значеннями випадкової величини (ознаки) Х: R = x max – x min.
2) Середнє лінійне абсолютне відхилення (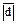 ): ):
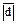 = M(|X – m Х|).
3) Дисперсія (D(Х), або D, або σ Х 2):
D = M((X – m Х)2).
4) Середнє квадратичне відхилення (СКВ, σ Х):
σ Х = √ D.
5) Інтерквартальна широта х 3/4 – х 1/4 і (10-90)-процентильна широта х 90/100 – х 10/100.
6) Півширота одномодального неперервного розподілу – піврізниця двох значень Х, у котрих f (X) = maxf(X) / 2 = f(m Х)/2. = M(|X – m Х|).
3) Дисперсія (D(Х), або D, або σ Х 2):
D = M((X – m Х)2).
4) Середнє квадратичне відхилення (СКВ, σ Х):
σ Х = √ D.
5) Інтерквартальна широта х 3/4 – х 1/4 і (10-90)-процентильна широта х 90/100 – х 10/100.
6) Півширота одномодального неперервного розподілу – піврізниця двох значень Х, у котрих f (X) = maxf(X) / 2 = f(m Х)/2.
|
| 11. Характеристики асиметрії й ексцесу | 1) Коефіцієнт асиметрії: 2) Коефіцієнт ексцесу:
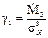 . . 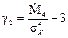 .
3) Пірсонівська міра асиметрії одномодального розподілу: .
3) Пірсонівська міра асиметрії одномодального розподілу:
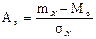 , , 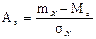 . .
|
| Типові теоретичні розподіли | |
12. Біноміальний розподіл b(k; N, p)
(Бернуллі)

| Розподіл (з параметрами N і p) ймовірностей дискретної випадкової величини Х, яка набуває невід’ємного цілого значення k з ймовірністю (інакше, ймовірність того, що випадкова подія трапляється k раз у N можливих випробуваннях):
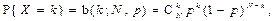 де
де 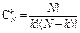 –
кількість k -елементних
сполучень;
p – імовірність події в
кожному випробуванні
(0 < p < 1).
Рис. Біноміальний розподіл
b(k; N, p) з N = 8 і p = 0,2. –
кількість k -елементних
сполучень;
p – імовірність події в
кожному випробуванні
(0 < p < 1).
Рис. Біноміальний розподіл
b(k; N, p) з N = 8 і p = 0,2.
|
Продовження таблиці 4
| 13. Умови, за яких розподіл Бернуллі зводиться до розподілу Пуассона | Якщо N → ∞, p → 0, а Np має скінченну границю λ > 0, то біноміальний розподіл зводиться до розподілу Пуассона (► п.4.14) (апроксимується останнім) з центром Np і дисперсією Np (закон «малих» чисел). |
14. Розподіл
 Пуассона
p(k; λ) Пуассона
p(k; λ)
| Розподіл (з фіксованим параметром λ = Np > 0) ймовірностей дискретної випадкової величини Х, яка набуває невід’ємного цілого значення k з ймовірніс-
тю:
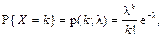 де p – імовірність події
в кожному випробуванні
(0 < p < 0,1).
Рис. Розподіл Пуассона з λ =0,5
де p – імовірність події
в кожному випробуванні
(0 < p < 0,1).
Рис. Розподіл Пуассона з λ =0,5
|
| 15. Умови, за яких біноміальний розподіл зводиться до нормального | Якщо N → ∞, 0 < (p = const) < 1, а Np → ∞, то біноміальний розподіл є асимптотично нормальним з центром Np і дисперсією Np (1 – p) (теорема Муавра-Лапласа, поодинокий випадок центральної граничної теореми). |
| 16. Нормальний розподіл (Гауса, або N -розподіл) (f(x)) | Розподіл ймовірностей неперервної випадкової величини Х з математичним сподіванням m Х і дисперсією σ Х2, який має щільність (крива розподілу – гаусіана):
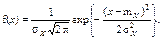
|
| 17. Стандартизована нормальна величина (и -розподіл) | Неперервна випадкова величина U = (X – m Х) / σ Х, яка має розподіл Гауса (представлена щільністю f(u) або функцією розподілу F(u)) з нульовим математичним сподіванням і одиничною дисперсією (гаусіаною):
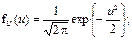 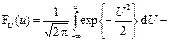 інтеграл Лебега-Стілтьєса.
В області визначення U від 0 до +∞ значення f(U) і F(U) представлені статистичними таблицями (► Д.3, 4).
інтеграл Лебега-Стілтьєса.
В області визначення U від 0 до +∞ значення f(U) і F(U) представлені статистичними таблицями (► Д.3, 4).
|
Продовження таблиці 4
| 17. и -розподіл (продовження) Рис. 1. Щільність стандартизованого нормального розподілу f(U). Рис. 2. Інтегральна функція стандартизованого нормального розподілу F(U). | 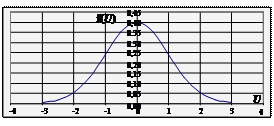


| |||||||||||||||||
| 18. Інтеграл ймовірностей Лапласа (Ф U (u)) (► Д.4) | Імовірність того, що неперервна випадкова величина U набуває значень в інтервалі від 0 до u (► п.4.17/рис.):
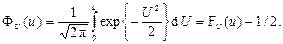
| |||||||||||||||||
| 19. Деякі властивості нормального розподілу | 1) f(±∞) → 0, f max (x) = f(m Х) = 1 /√ (2π),
f(x) = f U (u) / σ Х;
2) m Х = Mo = Me, γ1 = γ2 = 0;
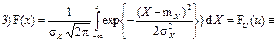
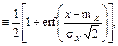 F(-∞) → 0, F(+∞) → 1,
функція похибок erf z ≡ -erf(- z) = 2F U (z √2) – 1; F(-∞) → 0, F(+∞) → 1,
функція похибок erf z ≡ -erf(- z) = 2F U (z √2) – 1;
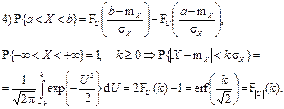
|
Продовження таблиці 4
| 19. Деякі властивості нормального розподілу (продовження) | Типові значення k і відповідні значення p: k = {1; 2; 3} і p = = {0,683; 0,954; 0,997}.
5) Квантилі, що обираються в якості довірчих границь U (α -значень U) (► п.п.4.17, 38, 39):
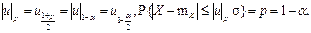 Типові α -значення U (α = {0,05; 0,01; 0,001}):
| u |0,95 = u 0,975 ≈ 1,96, | u |0,99 = u 0,995 ≈ 2,58, | u |0,999 = u 0,9995 ≈ 3,29.
6) Характеристики розсіювання:
- середнє абсолютне відхилення
M| X – m X | = σM| u | = √(2/π)σ ≈ 0,798σ.
- імовірне відхилення, або Me(| Х – m Х |):
| u |1/2σ Х = - u 1/4σ Х = u 3/4σ Х ≈ 0,674σ Х.
- половина півшироти: √(2ln2)σ ≈ 1,177σ.
- нижній і верхній квартилі:
x 1/4 = m X + u 1/4σ = m X – | u |1/2σ, x 3/4 = m X + u 3/4 = m X + | u |1/2σ.
- міра точності: h = 1/(σ√2).
Типові α -значення U (α = {0,05; 0,01; 0,001}):
| u |0,95 = u 0,975 ≈ 1,96, | u |0,99 = u 0,995 ≈ 2,58, | u |0,999 = u 0,9995 ≈ 3,29.
6) Характеристики розсіювання:
- середнє абсолютне відхилення
M| X – m X | = σM| u | = √(2/π)σ ≈ 0,798σ.
- імовірне відхилення, або Me(| Х – m Х |):
| u |1/2σ Х = - u 1/4σ Х = u 3/4σ Х ≈ 0,674σ Х.
- половина півшироти: √(2ln2)σ ≈ 1,177σ.
- нижній і верхній квартилі:
x 1/4 = m X + u 1/4σ = m X – | u |1/2σ, x 3/4 = m X + u 3/4 = m X + | u |1/2σ.
- міра точності: h = 1/(σ√2).
| ||||||
20. t -розподіл
(Стьюдента)
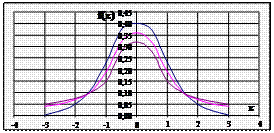
| Неперервна випадкова величина Х має t -розподіл з m ступенями свободи (m – натуральне число) в області визначення від -∞ до +∞, якщо щільність її ймовірності можна представити формулою
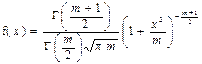 , ,
Г(1) = 1, Г(1/2) = √π.
Рис. Щільність t -розподілу для різних значень ступенів свободи m: 1) m = 1, 2) m = 2, 3) m = ∞ |
Продовження таблиці 4
| 20. t -розподіл (продовження) | Властивості розподілу:
1) f(±∞) → 0, f(- х) = f(+ х), maxf(X) = f(0).
2) Числові характеристики:
а) математичне сподівання М(Х) = 0 (m > 1);
б) дисперсія D(X) = m /(m – 2) (m > 2);
в) мода і медіана Мо = Ме = 0;
г) коефіцієнт асиметрії γ1=0 (m > 3);
ґ) коефіцієнт ексцесу γ2 = 3(m – 2)/(m – 4) (m > 4);
д) момент r -го порядку(r ≤ m – 1, m > 2)(відносно Х = 0).
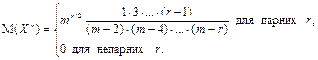 3) Типова інтерпретація. Якщо m випадкових величин X0, X1, …, Xm взаємно незалежні та нормально розподілені з нульовим математичним сподіванням і дисперсіями σ Х ², то випадкова величина
3) Типова інтерпретація. Якщо m випадкових величин X0, X1, …, Xm взаємно незалежні та нормально розподілені з нульовим математичним сподіванням і дисперсіями σ Х ², то випадкова величина
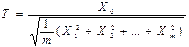 має t -розподіл з m ступенями свободи. T від σ Х ² не залежить.
4) Квантилі tm ; р = - tm ;1 -р за рахунок симетричності розподілу.
До того ж, |t | m ;1- α = tm ;1- α /2, що відповідає рівності P{| T | > | t |m;1 -α } = = α. Ці квантилі зведені у статистичні таблиці (► Д.6).
5) Наближення. Якщо m → ∞, тоді t -розподіл є асимптотично нормальним з центром 0 і дисперсією 1, так, що tm ; р ≈ uр, | t | m ;1 -α = t m ;1 -α/2 ≈ | u |1 -α = u 1 -α/2 для N > 30 (► п.п.4.33 і 6.8).
має t -розподіл з m ступенями свободи. T від σ Х ² не залежить.
4) Квантилі tm ; р = - tm ;1 -р за рахунок симетричності розподілу.
До того ж, |t | m ;1- α = tm ;1- α /2, що відповідає рівності P{| T | > | t |m;1 -α } = = α. Ці квантилі зведені у статистичні таблиці (► Д.6).
5) Наближення. Якщо m → ∞, тоді t -розподіл є асимптотично нормальним з центром 0 і дисперсією 1, так, що tm ; р ≈ uр, | t | m ;1 -α = t m ;1 -α/2 ≈ | u |1 -α = u 1 -α/2 для N > 30 (► п.п.4.33 і 6.8).
| ||||||||
21. χ² -розподіл
 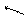 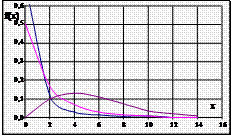 ( (   | Неперервна випадкова величина Х має χ² -розподіл з m ступенями свободи (m – натуральне число) в області визначення від -∞ до +∞, якщо щільність її ймовірності можна
представити формулою
 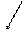  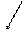 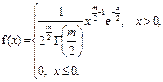
Рис. Щільність χ²-розподілу для різних значень ступенів свобо- ди m: 1) m = 1; 2) m = 2; 3) m = 6 |
Продовження таблиці 4
| 21. χ² -розподіл (продовження) | Властивості розподілу:
1) f(+∞) → 0.
2) Числові характеристики:
а) математичне сподівання М(Х) = m;
б) дисперсія D(X) = 2 m;
в) мода Мо = m – 2 (m ≥ 2);
г) коефіцієнт асиметрії γ1 = 2√(2/ m);
ґ) коефіцієнт ексцесу γ 2 = 12/ m;
д) момент r -го порядку (відносно Х = 0)
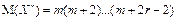 .
3) Типова інтерпретація. Якщо m взаємно незалежних стандартизованих випадкових величин Uj = (Xj – M(Xj))/σ Xj мають нормальні розподіли, то сума їх квадратів .
3) Типова інтерпретація. Якщо m взаємно незалежних стандартизованих випадкових величин Uj = (Xj – M(Xj))/σ Xj мають нормальні розподіли, то сума їх квадратів
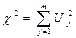 має χ² -розподіл з m ступенями свободи.
4) Квантилі χ²m ; p або χ²m ;1- α зведені у статистичні таблиці (► Д.5).
5) Наближення. Якщо m → ∞, тоді
- Х розподілена асимптотично нормально з центром m і дисперсією 2 m;
- Х / m розподілена асимптотично нормально з центром 1 і дисперсією 2/ m;
- √(2 X) розподілена асимптотично нормально з центром √(2 m – 1) і дисперсією 1, так, що
χ²m ; p ≈ 1/2(√(2 m – 1) + Up)²
для m > 30 (► п.п.4.33 і 6.8). Up – квантилі стандартизованого нормального розподілу. Ця апроксимація непридатна при p наближених до 0 або до 1. Кращою щодо цього є апроксимація
має χ² -розподіл з m ступенями свободи.
4) Квантилі χ²m ; p або χ²m ;1- α зведені у статистичні таблиці (► Д.5).
5) Наближення. Якщо m → ∞, тоді
- Х розподілена асимптотично нормально з центром m і дисперсією 2 m;
- Х / m розподілена асимптотично нормально з центром 1 і дисперсією 2/ m;
- √(2 X) розподілена асимптотично нормально з центром √(2 m – 1) і дисперсією 1, так, що
χ²m ; p ≈ 1/2(√(2 m – 1) + Up)²
для m > 30 (► п.п.4.33 і 6.8). Up – квантилі стандартизованого нормального розподілу. Ця апроксимація непридатна при p наближених до 0 або до 1. Кращою щодо цього є апроксимація
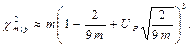
|
Продовження таблиці 4
22. F -розподіл
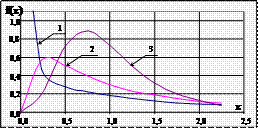 (Фішера) (Фішера)
| Неперервна випадкова величина Х має F -розподіл з k 1 і k 2 ступенями свободи (k 1 і k 2 – натуральні числа) в області визначення від -∞ до +∞, якщо щільність її ймовірностей можна представити формулою
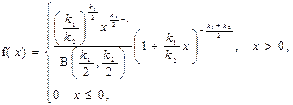 де В – бета-функція[25].
Рис.Щільність F-розподілу
для різних значень
с ступенів свободи k 1 і k 2:
1) k 1 = 1 і k 2 = 4;
2) k 1 = 4 і k 2 = 2;
3) k 1 = 10 і k 2 = 50
Властивості розподілу:
1) f(+∞) → 0.
2) Числові характеристики:
а) математичне сподівання М(Х) = k 2/(k 2 – 2) (k 2 > 2);
б) дисперсія D(X) = 2 k 2²(k 1 + k 2 – 2)/(k 1(k2 – 2)²(k 2 – 4)) (k 2 > 4);
в) мода Мо= k 2(k 1 – 2)/ k 1(k 2 + 2) (k 1 > 2);
г) момент r -го порядку (відносно Х = 0)
де В – бета-функція[25].
Рис.Щільність F-розподілу
для різних значень
с ступенів свободи k 1 і k 2:
1) k 1 = 1 і k 2 = 4;
2) k 1 = 4 і k 2 = 2;
3) k 1 = 10 і k 2 = 50
Властивості розподілу:
1) f(+∞) → 0.
2) Числові характеристики:
а) математичне сподівання М(Х) = k 2/(k 2 – 2) (k 2 > 2);
б) дисперсія D(X) = 2 k 2²(k 1 + k 2 – 2)/(k 1(k2 – 2)²(k 2 – 4)) (k 2 > 4);
в) мода Мо= k 2(k 1 – 2)/ k 1(k 2 + 2) (k 1 > 2);
г) момент r -го порядку (відносно Х = 0)
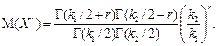 3) Типова інтерпретація. Якщо k 1 + k 2 взаємно незалежних випадкових величин Хi (i = 1, 2, …, k 1) і Xj (j = 1, 2, …, k 2) мають нормальні розподіли з центрами 0 і дисперсіями σ Х ², то відношення двох випадкових величин
3) Типова інтерпретація. Якщо k 1 + k 2 взаємно незалежних випадкових величин Хi (i = 1, 2, …, k 1) і Xj (j = 1, 2, …, k 2) мають нормальні розподіли з центрами 0 і дисперсіями σ Х ², то відношення двох випадкових величин
|
Продовження таблиці 4
| 22. F -розподіл (продовження) | 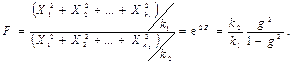 що мають χ ²-розподіли з k 1 і k 2 ступенями свободи відповідно, підпорядковано F -розподілу з k 1 і k 2 ступенями свободи. F від σ Х ² не залежить.
що мають χ ²-розподіли з k 1 і k 2 ступенями свободи відповідно, підпорядковано F -розподілу з k 1 і k 2 ступенями свободи. F від σ Х ² не залежить.
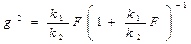 має бета-розподіл.
Змінна
має бета-розподіл.
Змінна 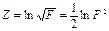 має щільність з розподілом Фішера: має щільність з розподілом Фішера:
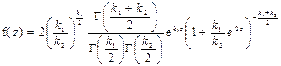 ;
4) Квантилі Fk 1, k 2;1 - α = 1/ Fk 2, k 1; α зведені у статистичні таблиці (► Д.7).
5) Наближення. Якщо k 1 → ∞, k 2 → ∞, тоді величина Z розподілена асимптотично нормально з центром (k 1 – – k 2)/(2 k 1 k 2) і дисперсією (k 1 + k 2)/(2 k 1 k 2). Ця апроксимація є придатною для k 1 > 30 і k 2 > 30 (► п.п.4.33 і 6.8). ;
4) Квантилі Fk 1, k 2;1 - α = 1/ Fk 2, k 1; α зведені у статистичні таблиці (► Д.7).
5) Наближення. Якщо k 1 → ∞, k 2 → ∞, тоді величина Z розподілена асимптотично нормально з центром (k 1 – – k 2)/(2 k 1 k 2) і дисперсією (k 1 + k 2)/(2 k 1 k 2). Ця апроксимація є придатною для k 1 > 30 і k 2 > 30 (► п.п.4.33 і 6.8).
|
| 23. Центральна гранична теорема (ЦГТ) (умови нормалізації розподілів) | Якщо випадкова величина являє собою суму N взаємно незалежних випадкових величин Хі (i = 1, …, N) із скінченними математичними сподіваннями m Хi і дисперсіями σ Хi 2, то при необмеженому збільшенні їх кількості (N → ∞) вона має асимптотично нормальний розподіл з центром Σm Хi і дисперсією Σσ Хi 2, до того ж, для будь-якого додатного числа ε існує границя (умови Ліндеберга):
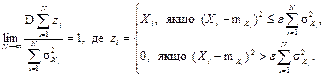 Якщо Хі мають один і той же самий розподіл ймовірностей із скінченим математичним сподіванням m Х і загальною дисперсією σ Х 2, то випадкова величина
Якщо Хі мають один і той же самий розподіл ймовірностей із скінченим математичним сподіванням m Х і загальною дисперсією σ Х 2, то випадкова величина 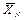 = (Х 1 + Х 2 + … + ХN)/ N має асимптотично нормальний розподіл ймовірностей з центром m Х і дисперсією σ Х 2/ N (теорема Ліндеберга-Леві). = (Х 1 + Х 2 + … + ХN)/ N має асимптотично нормальний розподіл ймовірностей з центром m Х і дисперсією σ Х 2/ N (теорема Ліндеберга-Леві).
|
Продовження таблиці 4
| § 4.3. Методологія статистичного аналізу(► рис.4.1) | |
| 24. Параметр і його оцінка | Таке уточнення параметра η розподілу статистичної ознаки Х в генеральній сукупності (► п.6.2), ідеалізованого певною імовірнісною моделлю F(Х) з тим же самим параметром, по даних (X 1, X 2, …, Xn) вибіркового дослідження (вибірки (► п.6.4)), що дає певну статистику (вибіркову оцінку (► п.6.10)) Y (X 1, X 2, …, Xn), яка надійно (► п.4.25) представляє цей параметр своїм значенням yj = y (x 1, x 2, …, xn) (j = 1, 2, …), отриманим по реалізації вибіркових даних (x 1, x 2, …, xn). Поширені оцінки – вибіркові частка та середнє арифметичне. Оцінка може бути точковою й інтервальною (► п.4.39). |
| 25. Властивості надійної оцінки | Шукана оцінка є надійною, якщо вона є слушною (► п.4.26), незміщеною (► п.4.27) й ефективною (► п.4.28). Вона може бути достатньо надійною, якщо задовольняє хоча б однієї з цих властивостей. |
| 26. Слушна оцінка | Така оцінка Y параметра η, яка при n → ∞ наближається по ймовірності до значення параметра η:
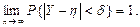 Різниця Δ j = yj – η є похибкою оцінювання і має випадковий характер.
Різниця Δ j = yj – η є похибкою оцінювання і має випадковий характер.
|
| 27. Незміщена оцінка | Така оцінка Y параметра η, математичне сподівання якої M(Y) дорівнює значенню параметра η:
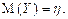 Величина |M(Y) – η | є зміщенням оцінки.
Величина |M(Y) – η | є зміщенням оцінки.
|
| 28. Ефективна оцінка | Така оцінка Y параметра η (обов’язково незміщена та слушна), дисперсія якої існує й є найменшою для асимптотично нормальних (► п.6.11/2) розподілів f(Y) із середнім η і дисперсією D(Y) = λ/ n:
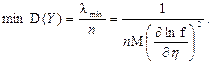 Відношення
Відношення 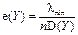 називають ефективністю оцінки Y. називають ефективністю оцінки Y.
|
Продовження таблиці 4
| 29. Аналітичне вирівнювання[26] статистичного розподілу | Процедура розповсюдження властивостей певного теоретичного розподілу ймовірностей випадкової величини на числові характеристики статистичного розподілу частоти (частості, щільності) досліджуваної ознаки з метою їх наближеного взаємного представлення (з певною ймовірністю або на певному рівні значущості (► п.4.35)). Типові інтерпретації: 1) представлення статистичного (емпіричного) ряду теоретичною функцією (гаусіаною, розподілом Пуассона й ін.) з параметрами, що дорівнюють аналогічним емпіричним числовим характеристикам закономірності (► п.4.5); 2) представлення основної тенденції розвитку в ряду динаміки (► п.7.15) та 3) факторного зв’язку між ознаками (► п.9.4) адекватною математичною функцією (► п.п.7.17 і 9.13) (відповідно трендом (► п.7.15) і лінією регресії (► п.9.10)) з використанням методу найменших квадратів (► п.п.7.16 і 9.12). |
| 30. Статистична гіпотеза | Припущення про певний можливий закон розподілу F(X) або f(X) статистичної ознаки Х у вибірковій сукупності, або про значущість вибіркової оцінки Y. Гіпотеза може бути простою і складною (► п.4.34). |
| 31. Перевірка статистичної гіпотези | Для перевірки статистичних гіпотез, які встановлюють деякі властивості теоретичного розподілу (η), оцінюється правдоподібність досліджуваної вибірки за умови, що для обчислення функції правдоподібності (► п.6.5) застосовується передбачувана щільність розподілу f(X). Перевірка виконується за певними статистичними критеріями, або критеріями статистичних гіпотез (► п.4.32). |
| 32. Критерій статистичної гіпотези | Нехай задана деяка фіксована вибірка об’єму n (► п.6.4); критерій статистичної гіпотези Н – це правило, що дозволяє спростувати або прийняти гіпотезу Н за умов вибірки { х 1, х 2, …, хn }. Кожен критерій визначає критичну множину (область) S «точок» (Х 1, Х 2, …, Хn): гіпотеза відкидається як хибна (спростовується), якщо вибірка { х 1, х 2, …, хn } належить критичній множині, або потрапляє в область малої правдоподібності, тобто вибіркова статистика Y (Х 1, Х 2, …, Хn) малоймовірна за обраною гіпотетичною функцією правдоподібності (► п.6.11/3), й вважається істинною у протилежному випадку. |
Продовження таблиці 4
 32. Критерій статистичної гіпотези (продовження) 32. Критерій статистичної гіпотези (продовження)
| Таке прийняття або відкидання гіпотези не дає логічного її доказування або спростовування. Тут можливі чотири ситуації:
а) гіпотеза Н є вірною та приймається згідно критерію;
б) гіпотеза Н є невірною (хибною) та відкидається згідно критерію;
в) гіпотеза Н є вірною, але відкидається згідно критерію (похибка першого роду (► п.4.35));
г) гіпотеза Н є невірною (хибною), але прийма-
ється згідно критерію (похибка другого роду).
Для будь-якої множини фактичних
значень параметрів η 1, η 2, … ймовірність
відкинути гіпотезу по даній критичній
області S дорівнює
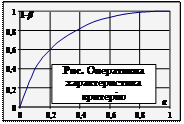
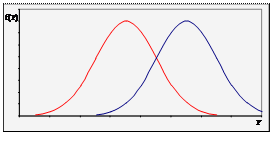
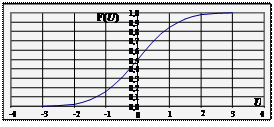
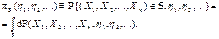 Якщо з гіпотезою Н конкурує лише одна альтернативна проста гіпотеза Н1 ≡ { η 1 = η 11, η 2 = η 21,…}, то ймовірність πS(η 11, η 21,…) відкинути гіпотезу Н, коли є вірною гіпотеза Н1, називають потужністю критерію, що визначений на S, по відношенню до гіпотези Н1. Залежність імовірності (1 – β) правильного відкидання гіпотези Н від імовірності α хибного її відкидання називають оперативною характеристикою критерію (рис.).
Якщо з гіпотезою Н конкурує лише одна альтернативна проста гіпотеза Н1 ≡ { η 1 = η 11, η 2 = η 21,…}, то ймовірність πS(η 11, η 21,…) відкинути гіпотезу Н, коли є вірною гіпотеза Н1, називають потужністю критерію, що визначений на S, по відношенню до гіпотези Н1. Залежність імовірності (1 – β) правильного відкидання гіпотези Н від імовірності α хибного її відкидання називають оперативною характеристикою критерію (рис.).
|
| 33. Кількість ступенів свободи критерію | Кількість «вільних» елементів даних, на які не накладені обмеження при обчисленні статистики вибірки або критерію перевірки. Інакше, це – кількість одиниць статистичної сукупності, які можуть набувати довільних значень, не змінюючи середнього значення ознаки. Наприклад, сукупність чотирьох (N = 4) вибіркових чисел 16, 21, 25, 30 дає середнє арифметичне число 23; їх відхилення від середнього становлять -7, -2, 2, 7 відповідно; сума відхилень дорівнює 0. Якщо необхідно зберегти значення середнього для інших чотирьох вибіркових чисел, лише три перших з них можуть набувати вільних значень, наприклад: 15, 22, 24, – четверте ж має бути таким, щоб забезпечити нульову суму чотирьох їх відхилень від середнього (-8 + (-1) + 1 + Δ4 = 0, Δ4 = 0 – (-8) – (-1) – 1 = 8, х 4 = 23 + 8 = 31). Отже, значення четвертого елемента сукупності, х 4 = 31, залежить від значень перших трьох її елементів, а тому кількість ступенів свободи m цього критерію (оцінки схожості чи відмінності величин середніх двох вибірок) з одним оцінюваним параметром, середнім арифметичним, (кількість параметрів s = 1) становить m = N – s = 4 – 1 = 3. |
Продовження таблиці 4
| 34. Проста та складна статистичні гіпотези | Статистична гіпотеза, яка однозначно визначає розподіл ймовірностей n -мірної величини (Х 1, Х 2, …, Хn) з параметрами η 1= η 10, η 2= η 20, …, що є координатами «точки» в просторі параметрів, вважається простою. У протилежному випадку (неоднозначна визначеність розподілу) гіпотеза є складною і обмежує «точки» η 1, η 2, … деякою областю в просторі параметрів. | ||||||||||||||||||||||||||||||||||
35. Рівень
значущості
критерію
 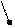   
  (α) (α)
| Бажано вибрати таку критичну область, щоб імовірність πS(η 1, η 2, …) була малою, якщо гіпотеза, яка перевіряється, є вірною, й значною в протилежному випадку. Нехай критична область S застосовується для перевірки простої гіпотези Н0 ≡ { η 1 = η 10, η 2 = η 20, …} («нульова гіпотеза»), і нехай вона є вірною, тоді ймовірність даремно відкинути гіпотезу Н0 (похибка першого роду) є πS(η 10, η 20, …) = α; α називають рівнем значущості даного


| ||||||||||||||||||||||||||||||||||
| 36. Правило Неймана-Пірсона відбору критеріїв для простих гіпотез | 1. Найбільш потужний критерій для простої гіпотези Н0 ≡ { η 1 = η 10, η 2 = η 20, …} відносно простої альтернативної гіпотези Н1 ≡ { η 1 = η 11, η 2 = η 21, …} визначається такою критичною областюS, яка дає найбільше значення ймовірності πS(η 11, η 21, …). 2. Рівномірно найбільш потужний критерій є найбільш потужним критерієм відносно всіх доступних альтернативних гіпотез; він не завжди існує. 3. Критерій є незміщеним, якщо πS(η 11, η 21, …) ≥ α для кожної простої альтернативної гіпотезиН1; в протилежному випадку критерій є зміщеним. Найбільш потужний незміщений критерій відносно даної альтернативної гіпотезиН1 і рівномірно найбільш потужний незміщений критерій відокремлюються з незміщених критеріїв. |
Продовження таблиці 4
| 36. Правило Неймана-Пірсона (продовження) | Критична областьS для найбільш потужного критерію будується так, щоб для всіх вибіркових точок (Х 1, Х 2, …, Хn) відношення правдоподібності f(Х 1, Х 2, …, Хn; η 10, η 20, …)/f(X 1, X 2, …; η 11, η 21, …) або р (Х 1, Х 2, …, Хn; η 10, η 20, …)/ р (X 1, X 2, …; η 11, η 21, …) було меншим за деяке постійне С; різні значення С даватиме «кращі» критичні області при різних рівнях значущості α. Рівномірно найбільш потужний критерій є доречним щодо перевірки гіпотези Н0 по відношенню до складної альтернативної гіпотези. Практично у виборі критерію переважаючою може стати легкість обчислень. Звичайно потужність критерію можна підвищити через збільшення об’єму вибірки n. | ||||
| 37. Критерій значущості | Нехай властивість ГСС, що перевіряється, зводиться до множини значень параметрів η 1 = η 10, η 2 = η 20, …, які порівнюються з вибірковими оцінками цих параметрів. В якості основи критерію намагаються побудувати таку статистику
Y = Y (Х 1, Х 2, …, Хn; η 10, η 20, …) ≡
≡g(Y 1, Y 2, …; η 10, η 20, …),
значення якої вимірюють відхилення або відношення порівнюваних параметрів генеральної сукупності (► п.6.9) й їх вибіркових оцінок (► п.6.10).
При цьому проста гіпотеза Н0 ≡ { η 1 = η 10, η 2 = η 20, …} відкидається із даним рівнем значущості α («відхилення» є значущим), якщо вибіркова оцінка Y потрапляє поза можливий інтервал { Yр 1 ≤ Y ≤ Yр 2} = р 2 – р 1 = = 1 – α. Відповідна оцінка параметра є незначущою. У протилежному випадку оцінка є значущою. Критерії, визначені в такий спосіб, називають критеріями значущості.
Остання формула визначає Yр 1 = Yр 1(&
Дата добавления: 2014-01-05; Просмотров: 552; Нарушение авторских прав?; Мы поможем в написании вашей работы! |
Генерация страницы за: 0.014 сек.









 область S
область S  перевіряє
перевіряє просту гіпотезу на
просту гіпотезу на рівні значущості α.
рівні значущості α.
 Рис. Перевірка гіпотези Н 0
Рис. Перевірка гіпотези Н 0 

