
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Узагальнюючі числові характеристики дискретного ряду
|
|
|
|
Задачі
Обчислення абсолютних (► п.5.1) і відносних (► п.5.2) величин.
Задача №10. Початкові умови. У травні в збиральному цеху виробничого підприємства з 10000 запланованих до збирання одиниць виробів були зібрані та передані на склад готової продукції 9997 одиниць, а 3 одиниці після їх технічної перевірки не відповідали ТУ і були відбраковані. У процесі збирання брали участь 200 працівників. У квітні цього ж самого року з 9005 запланованих до збирання в даному цеху одиниць виробів були зібрані 9000 одиниць стандартних виробів і 5 одиниць бракованих виробів. Після оновлення техно-
логічної лінії в червні звітного року собівартість збирання однієї одиниці знизилась з 10000 грн. до 9000 грн.
Завдання. Розрахувати: 1) відносну величину виконання планового завдання в квітні і травні поточного року, вважаючи виконаним завданням лише збирання стандартного виробу; 2) темп зростання кількості зібраних стандартних і бракованих виробів в травні порівняно з квітнем поточного року; 3) питому вагу стандартних і бракованих виробів, виготовлених в квітні, й аналогічні травневі показники; 4) відносну величину координації квітневих стандартних і бракованих виробів й аналогічні травневі показники; 5) порівняти собівартість виробу, зібраного на застарілій і новій технологічних лініях; 6) скільки виробів припадає в квітні та в травні на одного задіяного в їх збиранні працівника, а також скільки працівників припадає на 1000 (10000) одиниць зібраних ними виробів; 7) середньоденний обсяг збирання виробів квітня, травня та двох звітних місяців разом взятих; 8) середньомісячний відсоток браку; 9) середньоденну продуктивність праці одного працівника в квітні, травні та протягом двох місяців разом; 10) середню собівартість збирання одиниці виробу протягом звітного року, якщо на застарілій технологічній лінії було зібрано виробів на суму 468,10 млн.грн., а на новій – на суму 606,69 млн.грн..
Розв’язок. Вказані відносні величини розрахуємо по відповідних правилах (► рис. 5.2).
1) Відносна величина виконання планового завдання в квітні (к.) і травні (т.) поточного року обчислюється в процентах і складає відповідно
 |
|
 і
і
Квпзт.(%) = 9997: 10000 · 100% = 99,97%.
Рис. Стовпчикова діаграма % виконання плану
в квітні і травні звітного року
| Отже, на кожні 100 запланованих до збирання одиниць виробів припадає фактично зібраних одиниць (готових до експлуатації): в квітні – 99,94, а в травні – 99,97 (на 0,03 одиниці більше). |
Із-за наявності браку план і в квітні, і в травні не виконано на 0,06% (99,94% – 100% = - 0,06%) і 0,03% (99,97% – 100% = - 0,03%) відповідно.
2) Відносна величина динаміки (темп зростання) розраховується як процентне співвідношення кількості травневих і квітневих стандартних (с.) (бракованих (б.)) виробів:
Кд.с.(%) = 9997: 9000 · 100% ≈ 111,08% і Кд.б.(%) = 3: 5 · 100% ≈ 60,00%, –
тобто в травні поточного року стандартних виробів зібрано на 11,08% (111,08% – 100% = 40%) більше, ніж в лютому того ж самого року, або на кожні 100 одиниць стандартних виробів, зібраних в лютому, припадає 111,08
одиниць травневих стандартних виробів; щодо динаміки бракованих виробів, їх стало на 40% (60% – 100% = -40%) менше, або на кожні 100 квітневих бракованих виробів припадає 60 травневих.
3) Відносна величина структури розраховується як процентне співвідношення кількості стандартних (с.) або бракованих (б.) виробів і загальної кількості виробів відповідного місяця:
Кстр.с.к.(%) = 9000: 9005 · 100% ≈ 99,9445% і
Кстр.б.к.(%) = 5: 9005 · 100% ≈ 0,0555%;
Кстр.с.т.(%) = 9997: 10000 · 100% = 99,9700% і
Кстр.б.т.(%) = 3: 10000 · 100% = 0,0300%, –
тобто в квітні (травні) поточного року з кожних 100 одиниць виготовлених виробів стандартними є 99,9445 (99,97) одиниць, а бракованими – 0,0555 (0,03) одиниць. Сума кожної пари чисел має дорівнювати 100: 99,9445 + 0,0555 = 100 і 99,97 + 0,03 = 100 (умова нормування).
4) Відносна величина координації розраховується як співвідношення квітневої (травневої) кількості стандартних (с.) і бракованих (б.) виробів, взяте в довільному порядку, с./б. або б./с.:
Ккоорд.с./б.к. = 9000: 5 = 1800,00 і Ккоорд.б./с.к. = 5: 9000 ≈ 0,0006;
Ккоорд.с./б.т. = 9997: 3 = 3332,(33) і Ккоорд.б./с.т. = 3: 9997 ≈ 0,0003, –
тобто в квітні (травні) поточного року на кожну одиницю виробу, визнану бракованою, припадає 1800 (3332,(33)) одиниць стандартних виробів, або на кожну одиницю виробу, визнану стандартною, припадає 0,0006 (0,0003) одиниць бракованих виробів.
5) Відносна величина порівняння розраховується як співвідношення собівартості виробів, зібраних на застарілій (з.) і новій (н.) технологічних лініях:
Кп.з./н. = 10000: 9000 = 1,(11) і Кп.н./з. = 9000: 10000 = 0,90, –
тобто на кожну(-ій) гривню(-і) витрат на збирання виробу на новому (застарілому) обладнанні збирання цього виробу на застарілому (новому) обладнанні потребує 11 коп. додаткових витрат (заощаджує 10 коп.).
6) Відносна величина інтенсивності розраховується як співвідношення:
- зібраних в квітні (травні) виробів і кількості працівників, задіяних в їх збиранні:
Кінт.к. = 9005: 200 = 45,025 од./чол. і Кінт.т. = 10000: 200 = 50,000 од./чол., –
тобто на кожного працівника припадає по 45,025 одиниць зібраних (стандартних і бракованих) виробів у квітні та по 50 одиниць у травні (на 4,875 одиниці більше);
- кількості працівників і кількості зібраних ними в квітні (травні) одиниць виробів:
а) в проміле (‰) –
Кінт.к.(‰) = 200: 9005 · 1000‰ ≈ 22,21 чол./од. і
Кінт.т.(‰) = 200: 10000 · 1000‰ = 20,00 чол./од.;
б) в дециміле (‰ о) –
Кінт.к.(‰ о) = 200: 9005 · 10000‰ о ≈ 222,10 чол./од. і
Кінт.т.(‰ о) = 200: 10000 · 10000‰ о = 200,00 чол./од., –
тобто в квітні (травні) на кожну 1000 зібраних одиниць виробів припадає по 22,21 (20) працівників, а на кожні 10000 зібраних одиниць виробів припадає по 222,10 (200) працівників.
7) Середньоденний обсяг збирання стандартних виробів у поточному році становив:
- протягом квітня (30 днів)
nс.к. = 9000: 30 = 300,00 од./дн.,
- протягом травня (31 день)
nс.т. = 9997: 31 ≈ 322,48 од./дн.,
- протягом двох місяців, квітня і травня разом, (61 день)
n с.к.+т. = (9000 + 9997): (30 + 31) = 18997: 61 ≈ 311,43 од./дн.,
або через nс.к. і nс.т. як середнє арифметичне зважене
(вагою є кількість днів у місяці) –
n с.к.+т. = (300 · 30 + 322,48… · 31): (30 + 31) = 18997: 61 ≈ 311,43 од./дн., –
тобто з 9000, 9997 і 18997 одиниць стандартних виробів, зібраних відповідно в квітні, травні та протягом квітня і травня разом, кожного дня збиралось рівною мірою по 300, 322,48 і 311,43 одиниць.
8) Середньомісячний (протягом квітня і травня) відсоток браку можна обчислити в два способи: по-перше, як процентне відношення кількості бракованих виробів квітня і травня до загальної кількості зібраних в цей час виробів –
Кб.к.+т.(%) = (5 + 3): (9005 + 10000) · 100% ≈ 0,0421%;
по-друге, через квітневе Кстр.б.к.(%) і травневе Кстр.б.т.(%) значення відсотка браку при відомих значеннях загального обсягу щомісячного збирання, як зважене середнє арифметичне (► п.5.12), –
Кстр.б.к.+т.(%) = (0,0555… · 9005 + 0,03 · 10000): (9005 + 10000) =
= 0,0555… · 0,4738 + 0,03 · 0,5262 ≈ 0,0421%,
де 0,4738 (= 9005: (9005 + 10000)) і 0,5262 (=10000: (9005 + 10000)) – відповідно частка квітневого і травневого збирання у двомісячному (квітень і травень разом) звітному періоді (0,4738 + 0,5262 = 1 – умова нормування).
9) Середньоденну продуктивність праці одного працівника розрахуємо як відношення кількості зібраних протягом відповідного звітного періоду одиниць виробів до кількості задіяних у збиранні працівників і тривалості цього періоду:
- протягом квітня (30 днів)
tк. = 9005: 30: 200 ≈ 1,5008 од./чол.-дн.,
- протягом травня (31 день)
tт. = 10000: 31: 200 ≈ 1,6129 од./чол.-дн.,
- протягом двох місяців, квітня і травня разом, (61 день)
tк.+т. = (9005 + 10000): 61: 200 ≈ 1,5578 од./чол.-дн.,
або через tк. і tт. як середнє арифметичне зважене
(вагою є кількість днів у місяці) –
tк.+т. = (1,5008… · 30 + 1,6129… · 31): (30 + 31) = 95,0258…: 61 ≈ 1,5578 од./чол.-дн., -
тобто з 9005, 10000 і 19005 одиниць виробів, зібраних відповідно в квітні, травні та протягом квітня і травня разом, щоденно кожним працівником збиралось рівною мірою наближено по 1,5008, 1,6129 і 1,5578 одиниць.
10) Середня собівартість збирання одиниці виробу протягом звітного року може бути визначена як співвідношення загальної вартості зібраних протягом цього року виробів і їх кількості. Загальна вартість – це сума вартості виробів, зібраних на застарілій технологічній лінії, і вартості виробів, зібраних на новій технологічній лінії, тобто 468,10 + 606,69 = 1074,79 млн.грн. На застарілому обладнанні зібрано виробів у кількості, яка визначається співвідношенням відповідної вартості та собівартості: 468,10: 10000 = 0,046810 млн.од. (або 46810 од.). На новому обладнанні зібрано виробів у кількості, яка визначається співвідношенням відповідної вартості та собівартості: 606,69: 9000 = 0,067410 млн.од. (або 67410 од.). Отже, загальна кількість зібраних протягом звітного року виробів дорівнює 0,046810 + 0,067410 = 0,11422 млн.од. (або 114220 од.).
Таким чином, шукана величина собівартості визначається як середнє гармонічне (► п.5.14):
 = (468,10 + 606,69): (468,10: 10000 + 606,69: 9000) = 1074,79: 0,11422 ≈
= (468,10 + 606,69): (468,10: 10000 + 606,69: 9000) = 1074,79: 0,11422 ≈
≈ 9409,82 (грн.).
Вона характеризує те, що із 1074,79 млн.грн. загальної вартості 114220 одиниць виробів, зібраних на застарілій та новій технологічних лініях протягом звітного року, на збирання однієї одиниці виробу у середньому, на рівних, потрібно витрачати 9409,82 грн.
Якщо розглядати розраховані вище показники як результат звичайного відношення двох порівнюваних чисел, це – віднос-
ні величини. Якщо ці числа набувають конкретного змісту, так що показник характеризує розмір порівняної величини, що припадає на певну кількість одиниць бази порівняння, така відносна величина перетворюється на середню величину (► п.5.3), цілком властиву, закономірну для ознаки, яка в умовах сталого спостереження набуває великої кількості значень в межах досліджуваної статистичної сукупності.
Середнє – це один з розповсюджених прийомів узагальнення. Його важливість для статистичної практики та науки важко переоцінити. Ще в XVII ст. англійський економіст В.Петті (► Д.1.1) пропонував використовувати середнє як абстрактну, сталу міру характеристики одиниці сукупності (щодо вартості витрат на середньоденне харчування одного дорослого працівника), незважаючи на те, що в окремих одиниць значення цієї характеристики (ознаки) не співпадають із значенням середнього. Вчений уважав сталість середньої величини відображенням закономірності досліджуваних явищ й уможливлював реконструювання інформації через брак достатнього обсягу вихідних даних (метод непрямих розрахунків).
Яскравим вираженням поглядів на середнє є теорія «середньої людини» бельгійського математика А.Кетле (► Д.1.6), який ототожнював середню людину з ідеалом людства, а «це, – на думку видатного російського статистика Ю.Е.Янсона (► Д.2.14), – природно, приводить його до цілковито механічного погляду і на закони руху соціального життя: рух – це не є розвиток, а є поступове зростання середніх властивостей людини, поступове відновлення типу; отже, таке нівелювання всіх проявів життя соціального тіла, поза яким усякий поступовий рух припиняється» [37].
Середнє, як технічний прийом спрощення математичних обчислень, повсюдно використовували математичні статистики К.Пірсон (► Д.1.10), В.Госсет (► Д.1.11), Р.Фішер (► Д.1.12) й ін.
Сьогодні жодне соціальне, економічне дослідження не обходиться без статистичного середнього. Такі поняття, як «середня заробітна плата», «середня вартість споживчого кошику», «середня тривалість життя», «середні ціни», давно увійшли в наш щоденний ужиток.
З точки зору способів обчислення числових характеристик утворюваних вибіркових розподілів, несуцільні обстеження ні чим не відрізняються від суцільних спостережень до тих пір, поки не йде мова про оцінювання відповідних параметрів генеральних сукупностей (► гл.6).
Задача №11. Завдання. У варіаційному дискретному ряду, побудованому в задачі №3, визначити наступні числові характеристики закономірності розподілу місячних витрат на купівлю продуктів харчування 20-ти обстежених сімей:
- середнє арифметичне;
- структурні середні: а) моду та б) медіану;
- показники варіації: а) (абсолютний) розмах варіації; б) (середні) середнє лінійне абсолютне відхилення, дисперсію, середнє квадратичне відхилення; в) (відносні) коефіцієнт осциляції, відносне лінійне відхилення, коефіцієнт варіації;
- числові характеристики асиметрії й ексцесу.
Розв’язок.
Усі проміжні розрахунки зручно звести в розрахункову таблицю.
Розрахункова таблиця
| j | xj, грн. | fj | xj · fj, грн. | | xj –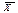 | · fj,
грн. | · fj,
грн.
| (xj –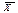 )² · fj,
грн.² )² · fj,
грн.²
| (xj –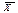 )³ · fj,
грн.³ )³ · fj,
грн.³
| (xj –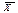 )4 · fj,
грн.4 )4 · fj,
грн.4
| |
| -1225043000 | ||||||||
| -912673000 | ||||||||
| -658503000 | ||||||||
| -456533000 | ||||||||
| -370386000 | ||||||||
| -50653000 | ||||||||
| -4913000 | ||||||||
| -1029000 | ||||||||
| Σ | x | |||||||
1) Середні витрати розрахуємо за формулою середнього арифметичного зваженого (► п.5.12 і з.№3/рис.):
 = (500 · 1 + 600 · 1 + 700 · 1 + 800 · 1 + 1000 · 2 + 1200 · 1 + 1400 · 1 +
= (500 · 1 + 600 · 1 + 700 · 1 + 800 · 1 + 1000 · 2 + 1200 · 1 + 1400 · 1 +
+ 1500 · 3 + 1700 · 1 + 1800 · 2 + 2000 · 2 + 2300 · 1 + 2400 · 1 +
+ 2700 · 1 + 3000 · 1): 20 = 31400: 20 = 1570,00 (грн.).
2) Структурні середні.
А) Модою є найчисельніші витрати (► п.5.17 і з.№3/рис.) – Мо = 1500 грн.
Б) Медіана ділить цей ряд за об’ємом навпіл (► п.5.20 і з.№3/рис.), зліва та справа від неї «знаходяться» по 10 сімей. Враховуючи те, що об’єм цього ряду є парним числом, медіана визначається як середнє арифметичне значень 10-ої й 11-ої одиниць упорядкованої за зростанням значень ознаки сукупності даних: Ме = (1500 + 1500): 2 = 1500 (грн.).
3) Показники варіації.
А) Абсолютний показник варіації, розмах варіації, розрахуємо як різницю максимального і мінімального значень витрат (► п.5.26 і з.№3/рис.):
R = 3000 – 500 = 2500 (грн.).
Б) Середні показники варіації:
- середнє лінійне абсолютне відхилення витрат розрахуємо за формулою зваженого СЛАВ (► п.5.28 і з.№3/рис.):
 = (|500 – 1570| · 1 + |600 – 1570| · 1 + |700 – 1570| · 1 + |800 – 1570| · 1 +
= (|500 – 1570| · 1 + |600 – 1570| · 1 + |700 – 1570| · 1 + |800 – 1570| · 1 +
+ |1000 – 1570| · 2 + |1200 – 1570| · 1 + |1400 – 1570| · 1 + |1500 – 1570| · 3 +
+ |1700 – 1570| · 1 + |1800 – 1570| · 2 + |2000 – 1570| · 2 + |2300 – 1570| · 1 +
+ |2400 – 1570| · 1 + |2700 – 1570| · 1 + |3000 – 1570| · 1): 20 = 11140: 20 =
= 557,00 (грн.);
- дисперсію витрат розрахуємо за формулою зваженої дисперсії (► п.5.30):
D = ((500 – 1570)² · 1 + (600 – 1570)² · 1 + (700 – 1570)² · 1 + (800 – 1570)² · 1 +
+ (1000 – 1570)² · 2 + (1200 – 1570)² · 1 + (1400 – 1570)² · 1 + (1500 – 1570)² · 3 +
+ (1700 – 1570)² · 1 + (1800 – 1570)² · 2 + (2000 – 1570)² · 2 + (2300 – 1570)² · 1 + + (2400 – 1570)² · 1 + (2700 – 1570)² · 1 + (3000 – 1570)² · 1): 20 = 9302000: 20=
= 465100,00 (грн.²);
- середнє квадратичне відхилення витрат розрахуємо як корінь квадратний з дисперсії (► п.5.32):
σ = √465100 ≈ 681,98 (грн.).
В) Відносні показники варіації:
- коефіцієнт осциляції (► п.5.34)
Ко = 2500: 1570 · 100 ≈ 159,24 (%);
- відносне лінійне відхилення (► п.5.35)
Кd = 557: 1570 · 100 ≈ 35,48 (%);
- коефіцієнт варіації (► п.5.36)
υ = 681,98: 1570 · 100 ≈ 43,44 (%).
4) Числові характеристики асиметрії й ексцесу.
А) Асиметрія:
- абсолютну асиметрію розрахуємо як різницю середнього арифметичного і моди (медіани) (► рис.5.4):
Δs = 1570 – 1500 = 70 (грн.);
- відносну асиметрію визначимо як Пірсонівську міру (► п.4.11/3):
Аs = (1570 – 1500): 681,98 ≈ 0,1026;
- процент асиметрії Ліндеберга (► рис.5.4) (зліва від середнього арифметичного значення витрат зосереджено 11 (k1 = 55%) одиниць сукупності)
γ1(%) = 55 – 50 = 5 (%);
- коефіцієнт асиметрії Ліндеберга (► п.4.11/1)
γ1 = ((500 – 1570)³ · 1 + (600 – 1570)³ · 1 + (700 – 1570)³ · 1 + (800 – 1570)³ · 1 +
+ (1000 – 1570)³ · 2 + (1200 – 1570)³ · 1 + (1400 – 1570)³ · 1 + (1500 – 1570)³ · 3 +
+ (1700 – 1570)³ · 1 + (1800 – 1570)³ · 2 + (2000 – 1570)³ · 2 + (2300 – 1570)³ · 1 +
+ (2400 – 1570)³ · 1 + (2700 – 1570)³ · 1 + (3000 – 1570)³ · 1): (20 · 681,98³) ≈
≈ 1833720000: 6343800326,334370 ≈ 0,289057;
- СКВ для γ1 становить (► п.6.16/4-е)
σ(γ1) = √(6 · (20 – 2): ((20 + 1) · (20 + 3))) ≈ 0,472866;
- співвідношення |γ1| і σ(γ1) дає
|γ1|/σ(γ1) = 0,289057: 0,472866 ≈ 0,6113.
Б) Ексцес:
- процент ексцесу Ліндеберга (► рис.5.4) (зліва та справа від середнього арифметичного значення витрат на відстані в половину СКВ зосереджено 7 (k2 = 35%) одиниць сукупності)
γ2(%) = 35 – 38,9 = -3,9 (%);
- коефіцієнт ексцесу Ліндеберга (► п.4.11/2)
γ2 = ((500 – 1570)4 · 1 + (600 – 1570)4 · 1 + (700 – 1570)4 · 1 + (800 – 1570)4 · 1 +
+ (1000 – 1570)4 · 2 + (1200 – 1570)4 · 1 + (1400 – 1570)4 · 1 + (1500 – 1570)4 · 3+
+ (1700 – 1570)4 · 1 + (1800 – 1570)4 · 2 + (2000 – 1570)4 · 2 + (2300 – 1570)4 · 1+
+ (2400 – 1570)4 · 1 + (2700 – 1570)4 · 1 + (3000 – 1570)4 · 1): (20 · 681,984) – 3 ≈
≈ 9996199400000: 4326360200000 – 3 ≈ -0,689467;
- СКВ для γ2 становить (► п.6.16/4-е)
σ(γ2) = √(24 · 20 · (20 – 2) · (20 – 3): ((20 + 1)² · (20 + 3) · (20 + 5))) ≈ 2,107324;
- співвідношення |γ2| і σ(γ2) дає
|γ2|/σ(γ2) = 0,689467: 2,107324 ≈ 0,3272.
Висновки. Із загальних 31400 грн. місячних витрат на купівлю продуктів харчування 20-ти обстежених сімей на кожну сім’ю у середньому, на рівних, припадає по 1570 грн. (середнє арифметичне значення витрат) (► з.№3/рис.).
Даний розподіл є одномодальним, мода становить 1500 грн., сімей з такими витратами – 3, більше, ніж сімей з іншими витратами. По 50% (по 10) сімей витрачають на продукти харчування менше та більше 1500 грн., саме таке значення має медіана (► з.№3/рис.).
Абсолютна розбіжність (розмах варіації) мінімальних (500 грн.) і максимальних (3000 грн.) витрат обстежених сімей становить 2500 грн. (► з.№3/рис.). Абсолютна відмінність витрат кожної сім’ї від середніх витрат (1570 грн.) на рівних становить 557 грн. (СЛАВ) (► з.№3/рис.), аналогічна квадратична міра дорівнює 681,98 грн. (СКВ), а їх відповідні відношення до середніх витрат, 35,48% (відносне лінійне відхилення) і 43,44% (коефіцієнт варіації), свідчать про те, що даний розподіл є кількісно неоднорідним (Кd > 32%), і варіація є суттєвою (υ > 40%).
Порівнюючи СЛАВ і СКВ, можна сказати, що за їх співвідношенням (557,00/681,98 ≈ 0,8167 (81,67%)) цей вибірковий розподіл можна наближено вважати нормальним. Для останнього воно становить 0,798 (► п.4.19/6), або майже 80%. Розбіжність є меншою за 5%. До того ж, відношення абсолютних значень коефіцієнтів асиметрії й ексцесу Ліндеберга до СКВ останніх становлять відповідно 0,6113 і 0,3272, що не перевищує трьох. Це дає підстави вважати асиметрію й ексцес несуттєвими, а розподіл за даними характеристиками – нормальним. Хоча, насправді, даний розподіл має правосторонню асиметрію (середнє арифметичне відрізняється від моди (медіани) на 70 грн., додатними є Пірсонівська міра асиметрії (0,1026), процент (5%) і коефіцієнт (0,289057) асиметрії Ліндеберга) і є плосковершинним (має від’ємні значення процента (-3,9%) і коефіцієнта (-0,689467) ексцесу Ліндеберга). Про наближеність даного розподілу до нормального свідчать також результати перевірки їх узгодженості за критерієм згоди А.М.Колмогорова в задачі №8.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 372; Нарушение авторских прав?; Мы поможем в написании вашей работы!