
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Узагальнюючі числові характеристики інтервального ряду
|
|
|
|
Задача №12. Завдання. У варіаційному інтервальному ряду, побудованому в задачі №4, визначити наступні числові характеристики закономірності розподілу місячних витрат на купівлю продуктів харчування 20-ти обстежених сімей:
- середнє арифметичне;
- структурні середні: а) моду та б) медіану;
- показники варіації: а) (абсолютний) розмах варіації; б) (середні) середнє лінійне абсолютне відхилення, дисперсію, середнє квадратичне відхилення; в) (відносні) коефіцієнт осциляції, відносне лінійне відхилення, коефіцієнт варіації;
- числові характеристики асиметрії й ексцесу.
Розв’язок.
Усі проміжні розрахунки зручно звести в розрахункову таблицю.
Розрахункова таблиця
| j | x н j –xв j , грн. | xj ´, грн. | fj | xj ´· fj, грн. | | xj ´ –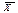 | ×
× fj, грн. | ×
× fj, грн.
| (xj ´ –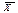 )² ×
× fj, грн.² )² ×
× fj, грн.²
| (xj ´ –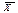 )³ ×
× fj, грн.³ )³ ×
× fj, грн.³
| (xj ´ –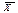 )4 ×
× fj, грн.4 )4 ×
× fj, грн.4
|
| 500-1000 | -2916000000 | |||||||
| 1000-1500 | -256000000 | |||||||
| 1500-2000 | ||||||||
| 2000-2500 | ||||||||
| 2500-3000 | ||||||||
| Σ | х | x |
1) Середні витрати розрахуємо через значення ознаки xj ´ у середині кожного інтервалу, умовно, за формулою середнього арифметичного зваженого (► п.5.13 і з.№4/рис.):
 = (750 · 4 + 1250 · 4 + 1750 · 6 + 2250 · 4 + 2750 · 2): 20 = 33000: 20 =
= (750 · 4 + 1250 · 4 + 1750 · 6 + 2250 · 4 + 2750 · 2): 20 = 33000: 20 =
= 1650,00 (грн.).
2) Структурні середні.
А) Модою є умовне значення витрат (► п.5.18 і з.№4/рис.) з модального інтервалу (► п.5.19), яким є третій, найчисельніший (f 3 = 6), інтервал:
Мо = 1500 + 500 · (6 – 4): (2 · 6 – 4 – 4) = 1750 грн.
Б) Медіана знаходиться в третьому інтервалі та ділить цей ряд за об’ємом навпіл (► п.5.21 і з.№4/рис.), зліва (справа) від неї «знаходяться» умовно по 10 сімей: в першому та другому разом – вісім (4 + 4) сімей, до 10-ти не вистачає двох сімей, які «відходять вліво» з третього інтервалу так, що
Ме = 1500 + 500 · (10 – 8): 6 ≈ 1666,67 (грн.).
3) Показники варіації.
А) Абсолютний показник варіації, розмах варіації, розрахуємо як різницю максимального і мінімального значень витрат (► п.5.26 і з.№4/рис.):
R = 3000 – 500 = 2500 (грн.).
Б) Середні показники варіації:
- середнє лінійне абсолютне відхилення витрат розрахуємо умовно, за формулою зваженого СЛАВ (► п.5.29):
 = (|750 – 1650| · 4 + |1250 – 1650| · 4 + |1750 – 1650| · 6 + |2250 – 1650| · 4 +
= (|750 – 1650| · 4 + |1250 – 1650| · 4 + |1750 – 1650| · 6 + |2250 – 1650| · 4 +
+ |2750 – 1650| · 2): 20 = 10400: 20 = 520,00 (грн.);
- дисперсію витрат розрахуємо умовно, за формулою зваженої дисперсії (► п.5.31):
D = ((750 – 1650)² · 4 + (1250 – 1650)² · 4 + (1750 – 1650)² · 6 + (2250 – 1650)² · 4
+ (2750 – 1650)² · 2): 20 = 7800000: 20 = 390000,00 (грн.²);
- середнє квадратичне відхилення витрат розрахуємо як корінь квадратний з дисперсії (► п.5.32):
σ = √390000 ≈ 624,50 (грн.).
В) Відносні показники варіації:
- коефіцієнт осциляції (► п.5.34)
Ко = 2500: 1650 · 100 ≈ 151,52 (%);
- відносне лінійне відхилення (► п.5.35)
Кd = 520: 1650 · 100 ≈ 31,52 (%);
- коефіцієнт варіації (► п.5.36)
υ = 624,50: 1650 · 100 ≈ 37,85 (%).
4) Числові характеристики асиметрії й ексцесу.
А) Асиметрія:
- абсолютну асиметрію розрахуємо як різницю середнього арифметичного і моди (медіани) (► рис.5.4):
Δs = 1650 – 1750 = -100 (грн.),
Δs = 1650 – 1666,67 = -16,67 (грн.);
- відносну асиметрію визначимо як Пірсонівську міру (► п.4.11/3):
Аs = (1650 – 1750): 624,50 ≈ -0,1601,
Аs = (1650 – 1666,67): 624,50 ≈ -0,0267;
- коефіцієнт асиметрії Ліндеберга (► п.4.11/1)
γ1 = ((750 – 1650)³ · 4 + (1250 – 1650)³ · 4 + (1750 – 1650)³ · 6 +
+ (2250 – 1650)³ · 4 + (2750 – 1650)³ · 2): (20 · 624,50³) =
= 360000000: 4871103122,5 ≈ 0,073905;
- СКВ для γ1 становить (► п.6.16/4-е)
σ(γ1) = √(6 · (20 – 2): ((20 + 1) · (20 + 3))) ≈ 0,472866;
- співвідношення |γ1| і σ(γ1) дає
|γ1|/σ(γ1) = 0,073905: 0,472866 ≈ 0,1563.
Б) Ексцес:
- коефіцієнт ексцесу Ліндеберга (► п.4.11/2)
γ2 = ((750 – 1650)4 · 4 + (1250 – 1650)4 · 4 + (1750 – 1650)4 · 6 +
+ (2250 – 1650)4 ·4 + (2750 – 1650)4 · 2): (20 · 624,504) – 3 =
= 6174000000000: 3042003900001,25 – 3 ≈ -0,970417;
- СКВ для γ2 становить (► п.6.16/4-е)
σ(γ2) = √(24 · 20 · (20 – 2) · (20 – 3): ((20 + 1)² · (20 + 3) · (20 + 5))) ≈ 2,107324;
- співвідношення |γ2| і σ(γ2) дає
|γ2|/σ(γ2) = -0,970417: 2,107324 ≈ 0,4605.
Висновки. Із загальних умовних 33000 грн. місячних витрат на купівлю продуктів харчування 20-ти обстежених сімей на кожну сім’ю у середньому, на рівних, припадає по 1650 грн. (середнє арифметичне значення витрат) (► з.№4/рис.).
Даний розподіл є одномодальним, мода становить 1750 грн., сімей з витратами від 1500 грн. до 2000 грн. – 6, більше, ніж сімей з іншими витратами. По 50% (по 10) сімей витрачають на продукти харчування менше та більше 1666,67 грн., саме таке умовне значення має медіана (► з.№4/рис.).
Абсолютна розбіжність (розмах варіації) мінімальних (500 грн.) і максимальних (3000 грн.) витрат обстежених сімей становить 2500 грн. (► з.№4/рис.). Абсолютна відмінність витрат кожної сім’ї від середніх витрат (1570 грн.) на рівних умовно становить 520 грн. (СЛАВ) (► з.№4/рис.), аналогічна квадратична міра дорівнює 624,50 грн. (СКВ), а їх відповідні відношення до середніх витрат, 31,52% (відносне лінійне відхилення) і 37,85%
(коефіцієнт варіації), свідчать про те, що даний розподіл є кількісно однорідним (Кd < 32%), і варіація є несуттєвою (υ < 40%).
Порівнюючи СЛАВ і СКВ, можна сказати, що за їх співвідношенням (520,00/624,50 ≈ 0,8327 (83,27%)) цей вибірковий розподіл можна наближено вважати нормальним. Для останнього воно становить 0,798 (► п.4.19/6), або майже 80%. Розбіжність є меншою за 5%. До того ж, відношення абсолютних значень коефіцієнтів асиметрії й ексцесу Ліндеберга до СКВ останніх становлять відповідно 0,1563 і 0,4605, що не перевищує трьох. Це дає підстави вважати асиметрію й ексцес несуттєвими, а розподіл за даними характеристиками – нормальним. Хоча, насправді, даний розподіл не є симетричним (середнє арифметичне відрізняється від моди (медіани) на -100 (-16,67) грн., від’ємною є також Пірсонівська міра асиметрії (-0,1601 і -0,0267), однак коефіцієнт асиметрії Ліндеберга є додатним (0,073905), що створює неоднозначність у визначенні сторонності асиметрії) і, до того ж, є плосковершинним (має від’ємне значення коефіцієнта ексцесу Ліндеберга (-0,970417)).
Перевірити наближеність даного розподілу до нормального можна за допомогою критерію згоди χ²-Пірсона, але його використання буде некоректним через недостатні значення інтервальної частоти, по-перше, і, по-друге, через додаткове перетворення дискретного розподілу на інтервальний.
Порівняльний аналіз числових характеристик двох рядів, дискретного й інтервального, побудованих на єдиних даних спостереження, свідчить про те, що аналогічні показники, по-перше, відрізняються один від одного, а, по-друге, іноді дають неоднозначне уявлення про кількісну однорідність (неоднорідність) розподілу, про суттєвість (несуттєвість) варіації, про бік асиметрії й ексцесу. Тому, обираючи спосіб систематизації даних у варіаційному ряду, необхідно пам’ятати:
1) об’єктивними є лише ті закономірності розподілу, які отримані по фактичному вихідному матеріалу;
2) будь-які перетворення даних спостереження, наприклад, з дискретних на інтервальні, дають суб’єктивну характеристику закономірностей розподілу ознаки.
Типологічні й аналітичні групування, що виконуються у варіаційних рядах, дозволяють застосовувати елементи дисперсійного факторного аналізу з метою виявлення тих факторів, які є переважаючими у варіації (► п.5.24) досліджуваної ознаки, а в подальшому і з метою статистичної оцінки факторного зв’язку між ознаками (► рис.5.1 і гл.9).
Види дисперсії (елементи дисперсійного аналізу) (► п.5.39).
Задача №13. Завдання. У варіаційному дискретному ряду, побудованому в задачі №3, знайти міжгрупову дисперсію, середнє внутрішніх групових дисперсій, загальну дисперсію, а також коефіцієнт детермінації щодо оцінки впливу типу місцевості (міська і сільська) 20-ти обстежених сімей на їх витрати на купівлю продуктів харчування, якщо ці витрати розподілились за типовою ознакою «тип місцевості проживання» наступним чином (таблиця).
Таблиця
Витрати на купівлю продуктів харчування (грн.) 20-и обстежених сімей N-ої обл.,
які проживають в сільській і міській місцевості
| Сільська місцевість(l = 1) | Міська місцевість(l = 2) |
| 500, 600, 700, 800, 1000, 1400, 1500, 1500, 2000, 2300 | 1000, 1200, 1500, 1700, 1800, 1800, 2000, 2400, 2700, 3000 |
Розв’язок.
Усі проміжні розрахунки зручно звести в розрахункову таблицю.
Розрахункова таблиця
| xj 1, грн. | fj 1 | xj 1 · fj 1, грн. | (xj 1 – )² · fj 1,
грн.² )² · fj 1,
грн.²
| xj 2, грн. | fj 2 | xj 2· fj 2, грн. | (xj 2 –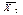 )² · fj 2, грн.² )² · fj 2, грн.²
|
| Σ | Σ |
1) Міжгрупову дисперсію (► п.5.41) розрахуємо через значення середніх витрат сімей кожної групи і через загальне середнє їх значення:
- середні витрати сільських сімей
 = (500 + 600 + 700 + 800 + 1000 + 1400 + 1500 ∙ 2 + 2000 + 2300): 10 =
= (500 + 600 + 700 + 800 + 1000 + 1400 + 1500 ∙ 2 + 2000 + 2300): 10 =
= 12300: 10 = 1230,00 (грн.);
- середні витрати міських сімей
 = (1000 + 1200 + 1500 + 1700 + 1800 ∙ 2 + 2000 + 2400 + 2700 + 3000): 10=
= (1000 + 1200 + 1500 + 1700 + 1800 ∙ 2 + 2000 + 2400 + 2700 + 3000): 10=
= 19100: 10 = 1910,00 (грн.);
- загальні середні витрати становлять 1570,00 грн. (► з.№11/1).
Отже, міжгрупова дисперсія
δ² = ((1230 – 1570)² ∙ 10 + (1910 – 1570)² ∙ 10): (10 + 10) = 2312000: 20 =
= 115600 (грн.²).
2) Середнє внутрішніх групових дисперсій (► п.5.42) розрахуємо через значення дисперсій витрат кожної окремої групи:
- дисперсія витрат сільських сімей
σ1² = ((500 – 1230)² + (600 – 1230)² + (700 – 1230)² + (800 – 1230)² +
+ (1000 – 1230)² + (1400 – 1230)² + (1500 – 1230)² ∙ 2 + + (2000 – 1230)² +
+ (2300 – 1230)²): 10 = 3361000: 10 = 336100,00 (грн.²);
- дисперсія витрат міських сімей
σ2² = ((1000 – 1910)² + (1200 – 1910)² + (1500 – 1910)² + (1700 – 1910)² +
+ (1800 – 1910)² ∙ 2 + (2000 – 1910)² + (2400 – 1910)² + (2700 – 1910)² +
+ (3000 – 1910)²): 10 = 3629000: 10 = 362900,00 (грн.²);
Отже, середнє внутрішніх групових дисперсій
 = (336100 ∙ 10 + 362900 ∙ 10): (10 + 10) = 6990000: 20 = 349500,00 (грн.²).
= (336100 ∙ 10 + 362900 ∙ 10): (10 + 10) = 6990000: 20 = 349500,00 (грн.²).
3) Загальна дисперсія (► п.5.40) становить 465100 грн.² (► з.№11/3-б).
Перевіримо виконання правила додавання дисперсій (► п.5.43), відповідно до якого загальна дисперсія визначається як сума міжгрупової дисперсії і середнього внутрішніх групових дисперсій. Насправді, 115600 + 349500 = = 465100.
4) Значення коефіцієнта детермінації (► п.5.44) визначимо як співвідношення міжгрупової та загальної дисперсій:
η² = 115600: 465100 ≈ 0,2485 (24,85%), –
яке свідчить про те, що лише 24,85% варіації витрат на купівлю продуктів харчування обумовлені впливом місцевості проживання, а решта (75,15%) – впливом інших факторів, наприклад, розміром доходів, кількістю членів сім’ї.
На відміну від множинних ознак, аналіз яких проведений вище, існують альтернативні ознаки (► п.п.1.2/б і 3.10). Аналіз закономірностей останніх дещо відрізняється.
Узагальнюючі числові характеристики (► п.п.5.15, 45) альтернативної ознаки (► п.3.10).
Задача №14. Завдання. За умов задачі №6 розрахувати середнє і дисперсію альтернативної ознаки «стать», якщо серед 43 членів 20-ти обстежених сімей 23 – жінки і 20 – чоловіки.
Розв’язок.
Позначимо наявність жіночої статі одиницею (1), а чоловічої – нулем (0).
Середнє значення (► п.5.15) та дисперсію (► п.5.45) альтернативної ознаки «стать» визначимо через питому вагу жінок і чоловік серед 43-ох обстежених:
 ω 1 = 23: 43 ≈ 0,534884 і ω о = 20: 43 ≈ 0,465116 (0,534884 + 0,465116 = 1).
ω 1 = 23: 43 ≈ 0,534884 і ω о = 20: 43 ≈ 0,465116 (0,534884 + 0,465116 = 1).
1) Середнє  ≈ 0,534884.
≈ 0,534884.
2) Дисперсія σ ω ² ≈ 0,534884 ∙ 0,465116 ≈ 0,248783.
Рис. Кругова діаграма структури сукупності 43-х
обстежених за ознакою «стать»:
група «0» – чоловіки; група «1» – жінки
Якщо через одиницю представити наявність чоловічої статі, то середнє зміниться з 0,534884 на 0,465116, а дисперсія залишається такою ж самою. Це пов’язано з тим, що середнє альтернативної ознаки, з одного боку, є відносною величиною структури і характеризує питому вагу значення ознаки у статистичній сукупності (рис.), в даному випадку – 23-ох жінок серед 43-ох обстежених, а, з іншого боку, ця характеристика має зміст середнього та характеризує, скільки одиниць даної ознаки припадає на відповідну кількість одиниць сукупності, в даному випадку з кожної умовної сотні обстежених 53,4884 – жінки (53,4884%).
У неоднозначності середнього значення альтернативної ознаки закладене глибоке філософське розуміння: дуальність нашого світу накладає відбиток і на числові характеристики його закономірності.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 470; Нарушение авторских прав?; Мы поможем в написании вашей работы!