Формування динамічних характеристик

Будь-яка система автоматичного керування, крім заданої точнос-ті регулювання в усталених режимах, повинна забезпечити такі якісні показники як час регулювання, перегулювання й число коли-вань. Їх можна визначити за відомою перехідною характеристикою, яка представляє собою реакцію системи на стрибкоподібну зміну задаючого сигналу чи збурення (ударне навантаження).

Система автоматичного регулювання швидкості електропривода повинна бути такою, щоби забезпечити технічно-оптимальний пе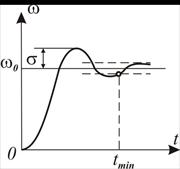рехідний процес, який характеризується мінімально можливим часом регулювання 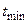при перегулюванні 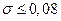і числі коливань за час 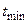менше двох (рис.9.3). Сформувати такий перехідний процес можна за допомогою корегувальних ланок, які можна визначити на підставі аналізу диференціального рівняння, яким описується динамічний процес в си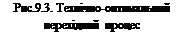с-темі.

Система рівнянь (9.1) описує уста-лений режим. Щоби скласти систему рівнянь, які описують динамічні процеси, необхідно рівняння (9.1) доповнити членами, що визначають кількісно зміну енергії в ланках. З врахуванням цього динаміка системи, наведеної на рис.9.1, буде описуватись наступною системою рівнянь:

;

;

;

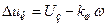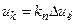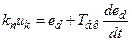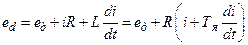; (9.8)

;

; ;

,

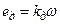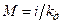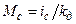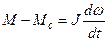де 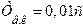– стала часу керованого перетворювача, яка врахо-вує інерційність системи імпульсно-фазового керування; 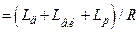– стала часу якорного кола; 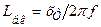– індуктивність трансформатора, приведена до вторинної обмотки; 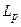– індуктивність згладжуючого реактора; 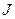– приведений до валу двигуна момент інерції привода.

Після відповідних перетворень (9.8) отримаємо диференціальне рівняння третього порядку

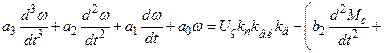
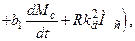(9.9)

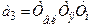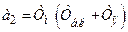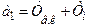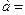
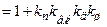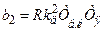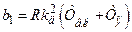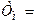
де ; ; ; ; ; ; 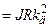– електромеханічна стала часу привода.

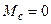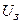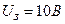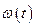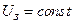Розв’язок (9.9) при є кривою перехідного процесу, зумо-вленого зміною задаючої напруги. Якщо напругу стрибком змі-нити від нуля до , то розв’язком (9.9) буде – крива зміни швидкості при пуску електропривода до швидкості . Роз-в’язок (9.9) при і зміні моменту навантаження 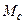представлятиме зміну швидкості, зумовлену зміною навантаження. Але ці процеси, зазвичай, не будуть технічно-оптимальними. Щоби переконатись у цьому, потрібно знайти розв’язок 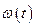, побудувати криву 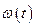і порівняти її з технічно-оптимальною кривою (рис.9.3).

Це дуже копітка робота. Тому розроблені методи, які дозволяють за відомими коефіцієнтами лівої частини рівняння (9.9) визначити час перехідного процесу і перегулювання.

Найбільше простим із відомих методів є використання діаграми Вишнеградського, з якої слідує, що технічно-оптимальний процес в системі автоматичного регулювання, яка описується диференціаль-ним рівнянням ІІІ-го порядку, буде тоді, коли коефіцієнти нормова-ною характеристикою рівняння

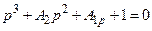(9.10)

будуть такими: 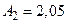і 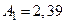[7, табл.10.5].

Коефіцієнти 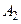і 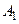зв’язані з коефіцієнтами рівняння (9.9) фор-мулами:

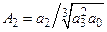і 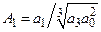. (9.11)

Тому необхідно за відомими коефіцієнтами 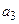, , 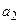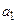і 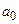рів-няння (9.9) визначити коефіцієнти 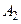і 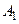і порівняти їх з наведе-ними. Якщо обчислені за формулами (9.11) коефіцієнти будуть від-різнятися від оптимальних значень, то необхідно доповнити систе-му керування корегувальними ланками. Змінити коефіцієнти рівня-ння (9.9) при першій і другій похідних можна введення від’ємних зворотних зв’язків за відповідними похідними з коефіцієнтами про-порційност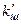і і 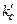(рис.9.4).

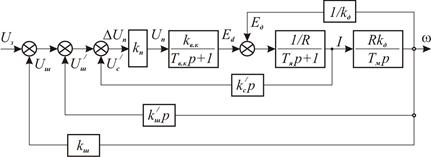
Рис.9.4. Структурна схема системи регулювання швидкості електропривода з корегувальними ланками

При подачі на вхід сумуючого підсилювача додатково напруг зворотних зв’язків за похідними

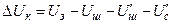. (9.12)

Тому, замінивши в (9.8) перше рівняння рівнянням (9.12), одер-жимо нову систему рівнянь, спростивши яку матимемо рівняння, аналогічне (9.9), але з такими коефіцієнтами:

; ;

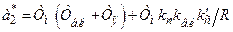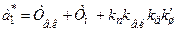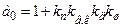; ; (9.13)

; .

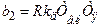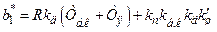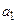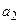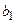З (9.13) слідує, що введення зворотних зв’язків за похідними призвело лише до зміни коефіцієнтів , і рівняння (9.9).

Коефіцієнти 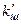і 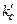тепер можна визначити з рівнянь:

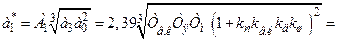
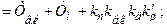
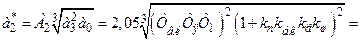
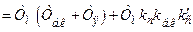. (9.14)

Зворотні зв’язки за похідними з визначеними коефіцієнтами 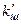і 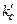забезпечать технічно-оптимальний перехідний процес в систе-мі, структурна схема якої наведена на рис.9.4.

Перевірку розрахунків слід провести моделюванням, використа-вши спеціалізований пакет МАTLAB Simulink або програму SIAM. Але реалізувати ідеальні диференціальні ланки з передавальною функцією 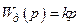в моделі не можна. Тому їх замінюють реальними диференціальними ланками з передавальними функціями 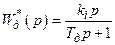, прийнявши 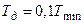, де 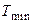– найменша стала часу в контурі регулювання.

Дата добавления: 2014-01-05