Моделлю

Безпошукова адаптивна система керування з еталонною

БАС з еталонною моделлю використовується в основному тоді, коли необхідно забезпечити бажані статичні і динамічні показники роботи системи при зміні її параметрів шляхом зміни параметрів регулятора (коефіцієнта підсилення, сталих часу чи формування додаткових впливів).

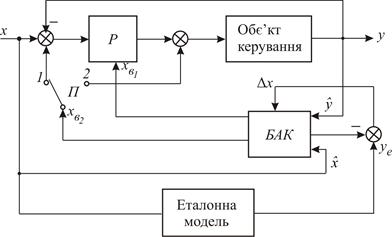
Рис. 14.1. Безпошукова адаптивна система з еталонною моделлю

Зміну параметрів регулятора чи додаткові впливи здійснює блок адаптивного керування БАК, на вхід якого подаються вимірювані значення вхідної і вихідної величини.

У складі БАК може бути пристрій, котрий оцінює недоступні вимірюванню змінні, наприклад, активний опір обмотки якоря чи ротора, і формує вихідний вплив , величина і знак якого зале-жать від відхилення вихідної змінної 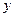від вихідної змінної еталон-ної моделі в установленому режимі.

Вихідний адаптивний вплив спричиняє зміну параметрів ре-гулятора Р, а вплив – може подаватись на вхід чи на вихід регу-лятора в залежності від положення перемикача П (рис.14.1). Порівняння вихідних змінних з об’єкта керування і еталонної моделі відбувається безперервно і безперервно БАК формує відповідні впливи на регулятор, який протидіє відхиленню 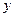від на величину, більшу зони нечутливості БАК. В результаті вихідна змінна об’єкта не буде виходити за межі «коридора», показаного на рис. 14.2 пунктирними лініями, і мо-же відхилятись від ви-хідної змінної еталонної моделі (крива 1 на рис. 14.2). Для змен-шення ширини «коридора» слід формувати і ще вплив, пропорційний похідній .

Якби не було БАК, то при зміні параметрів об’єкта керування перехідні процеси мо-гли бути з перерегулюванням (крива 2) чи без нього, але з великим часом регулювання (крива 3).

В якості еталонної моделі можна вибрати ланку другого порядку, яка буде описуватись диференціальним рівнянням

, (14.1)

де – коефіцієнт затухання; – власна частота коливань, .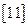

При початкових умовах і розв’язки (14.1) у відносних одиницях представлено сімейством кривих (рис. 14.3). Графічне представлення вихідної величини еталонної моделі наглядно показує, до якої кривої необхідно наближати перехідний процес в адаптивній системі керування, і спрощує визначення коефіцієнтів рівняння (14.1) за вибранимиі . При цьому усталене значення

,

де – коефіцієнт підсилен-ня розімкненої системи з одиничним зворотним зв’язком. Вибравши еталонний перехідний процес, необхідно перевірити чи зможе його реалізувати двигун, момент якого завжди обмежений величиною 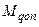за умови, що . Очевидно, що максимальне значення розрахункового моменту , визначеного за кривою , повинно задовільняти умову

. (14.2)

Вираз (14.2) називається 1-ю умовою реалізації закону 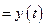. Величину можна визначити, підставивши в рівнян-ня руху електропривода значення у точці . Розв’язок (14.1) залежить від коренів характеристичного рівняння 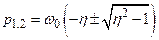, які можуть бути комплексно-спряженими 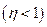, кратними і дійсними .

У випадку комплексних коренів

(14.3)

і першу умову реалізації функції отримаємо у виді

, (14.4)

де 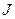– максимальний момент інерції електропривода; .

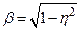У випадку дійсних коренів (аперіодичний перехідний процес)

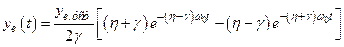(14.5)

і умова (14.2) матиме вид:

, (14.6)

де .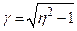

Коли 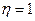, то

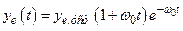(14.7)

і

. (14.8)

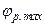Електропривод таких виробничих механізмів як швидкісні ліфти, важкі верстати та інші повинен забезпечити не тільки обмеження моменту (прискорення), але і зміну прискорення – ривка, величи-ною . Тому величина для вибраної не повинна перевищувати . Умова

(14.9)

називається 2-ю умовою реалізації .

Для наведених на рис.14.3 кривих умови /14.9/ будуть такими:

Ø для

, (14.10)

де ;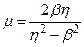

Ø для

;

(14.11)

Ø для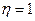

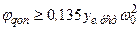(14.12)

Отримані формули для визначення допустимого моменту і ривка дозволяють не тільки перевірити умови реалізації адаптивного ке-рування, але і визначити , тобто час регулювання, який буде за-довольняти вказаним умовам.

Дата добавления: 2014-01-05