Дискретні передавальні функції і структурні схеми

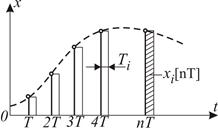Математичною основою опису динаміки електропривода з ЦСК без врахування квантування за рівнем є теорія імпульсних систем, оскільки неперервний сигнал перетворюється у квантований за часом імпульсний сигнал з амплітудно-імпульсною модуляцією з . При цьому амплітуда імпульсу дорівнює миттєвому значенню 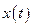на початку періоду дискретності 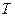(рис. 16.3).

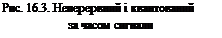За послідовність імпульсних сигналів перетво-рюється у так звану решітчас-ту функцію , цілечисельний аргумент якої визначається номером такта 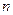часової дискретності. Розрахун-ки імпульсних систем, як і систем аналогових, проводять з ви-користанням перетворення Лапласа, але у формі дискретного 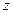- пе-ретворення:

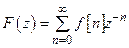, (16.11)

де 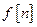– решітчаста функція – оригінал; – зображення ре-шітчастої функції; .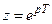

Пристрій, який формує послідовність імпульсів в залежності від вхідного сигналу, називається імпульсним елементом. Миттєвий імпульс представляють дельта-функцією:

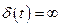при ;

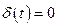при 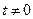, (16.12)

зображення якої 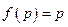. Згідно (16.12) імпульсний елемент опи-сується рівняннями

при ;

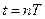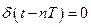при 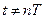. (16.13)

Зображення його вихідного сигналу

. (16.14)

За умови імпульсний елемент представляють ланкою перетворення неперервного сигналу 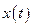у послідовність імпульсів і екстраполятора (рис.16.4), вихідна величина якого

. (16.15)

Зображенням (16.15) є функція

,

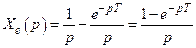оскільки зображенням за Лапласом одиничної функції 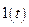є .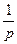

За вхідного сигналу передавальна функція екстраполятора

. (16.16)

Екстраполятор разом з неперервною ланкою називають приведе - ною ланкою, передавальна функція якої

, (16.17)

де – передавальна функція неперервної ланки.

Остання ланка на рис. 16.4 здійснює перетворення вихідного сиг-налу неперервної ланки у решітчасту функцію .

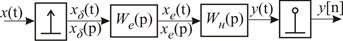
Рис. 16.4. Структурна схема імпульсного елемента і неперервної ланки

Застосувавши 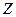-перетворення до (16.17), отримаємо дискретну передавальну функцію приведеної ланки:

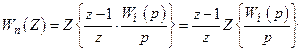. (16.18)

Оскільки 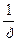є зображення функції 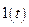, то є зображе-нням перехідної функції неперервної ланки, тобто це реакція неперервної ланки на одиничний імпульс. Отже, можна записати, що 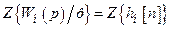і дискретна передавальна функція

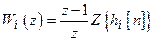, (16.19)

де – перехідна решітчаста функція неперервної ланки.

На підставі структурної схеми на рис. 16.4 складають структурну схему замкненого контуру цифрової системи керування електро-приводом (рис. 16.5). Неперервною ланкою у цій схемі є об’єкт ке-рування з передавальною функцією 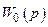, вихідною змінною якою може бути струм, момент, кутова швидкість чи переміщення.

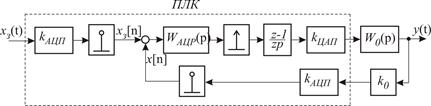
Рис. 16.5. Структурна схема цифрового контуру регулювання

Для даної структурної схеми дискретна передавальна функція приведеної ланки

. (16.20)

Дискретна передавальна функція розімкненого контуру

, (16.21)

де – дискретна передавальна функція цифрового регулято-ра.

Щоби визначити динамічні показники наведеної системи регу-лювання, необхідно розрахувати перехідну функцію замкненого контуру 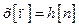для вхідного сигналу , за якою визначають перерегулювання і час регулювання. Дійсний перехідний процес 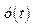розраховують за передавальною функцією замкненої системи

, (16.22)

використавши формули розкладання функції , або методом різницевих рівнянь.

Дата добавления: 2014-01-05