Синтез цифрового регулятора і його реалізація

Зазвичай, при синтезі цифрового регулятора, як і аналоговою, є відомою приведена цифрова передавальна функція . За цієї умови задаються динамічними показниками у виді бажаної неперер-вної перехідної функції замкненого контуру . Цю функцію для вибраного періоду квантування 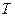переводять у решітчасту . Бажана дискретна передавальна функція контуру згідно (16.19)

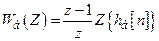. (16.23)

Бажана дискретна передавальна функція розімкненого контуру

. (16.24)

Тоді згідно (16.21) дискретна передавальна функція цифрового регулятора з врахуванням (16.20)

.

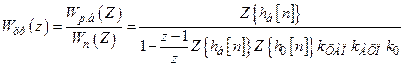(16.25)

Рівняння (16.25) визначає тип і параметри цифрового регулято-ра. Якщо обчислення передавальної функції за (16.25) складне, то за умови, що період квантування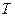

, (16.26)

де – час досягнення вихідним сигналом рівня 95% від устале-ного значення при подачі на вхід силової частини електропривода ступінчастого сигналу, цифровий регулятор можна представити різ-ницевим рівнянням, яке є прототипом диференціального рівняння.

Найбільш досконалим є ПІД-регулятор, алгоритм дії якого опи-сується рівняння

, (16.27)

де 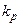– коефіцієнт підсилення регулятора 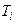і – відповідно ста-лі інтегрування і диференціювання. Щоби перетворити диференціа-льне рівняння (16.27) у різницеве, потрібно похідну замінити різни-цею першого порядку, а інтеграл – сумою. Обчислення дискретної суми складне в реалізації, тому його можна уникнути, про диферен-ціювавши (16.27).

В результаті одержимо

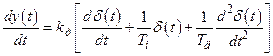. (16.28)

Аналогом диференціала І-го порядку неперервної функції є пер-ша обернена різниця

і ІІ-го порядку обернена різниця

.

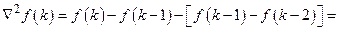
Підставивши різницеві обернені різниці в (16.28), отримаємо

або

, (16.29)

де ; ; .

Розрахунок величини керуючої дії на кожному такті пот-рібно проводити у відповідності з (16.29), тобто до попереднього значення керуючої дії треба добавити величину приросту, обчислену на інтервалі квантування:

, (16.30)

де . За алгоритма (16.30) обчислюється тільки поточний приріст керуючої дії і тому цей алго-ритм називають швидкісним.

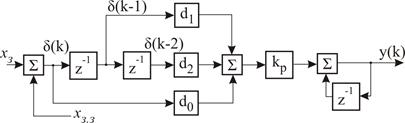
Рис. 16.6. Структурна схема швидкісного ПІД-регулятора

На структурній схемі через позначена ланка затримки сигна-лу на один період квантування. Наведена схема спрощує написання програми реалізації цифрового регулятора на базі ПЛК. Для зберіга-ння керуючої дії можна використати регістр-накопичувач, а для зберігання трьох послідовних вибірок змінних , 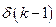і 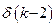– три послідовні комірки пам’яті даних. Оскільки регуля-тор повинен бути перенастроюваним, то для збереження коефіцієн-тів , , 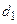і 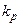можна використати чотири послідовні комірки оперативної пам’яті.

Отже, згідно (16.30) синтез цифрового регулятора зводиться до визначення коефіцієнтів ,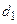і , величина яких залежить від періоду квантування 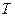, і коефіцієнта підсилення регулятора 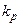. Встановлено, що величина 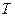впливає на похибку регулювання: чим менша 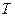, тим більше дискретний закон регулювання набли-жається до неперервного, який описується рівнянням (16.27). Але зменшення періоду квантування вимагає зменшення часу обчислен-ня керуючої дії на кожному такті і призводить до збільшення впли-ву завад. Тому необхідно шукати компромісне рішення.

Американські вчені Зіглер і Нікольс рекомендують приймати , де – період критичних коливань об’єкта керування. За такого вибору 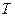рекомендують такі співвідношення:

і . (16.31)

Тоді залишається визначити лише коефіцієнт підсилення регуля-тора 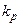, який знаходять за монограмами, 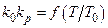, де і – відповідно коефіцієнт передачі і стала часу об’єкта керування .

Цифрові системи керування мають такі переваги у порівнянні з аналоговими як простота задання програми і зміни алгоритма, висока надійність і завадостійкість, малі габарити і висока ступінь інтеграції. Це сприяє їх широкому застосуванню в електроприводах багатьох виробничих механізмів.

Дата добавления: 2014-01-05