Решение. По 12 транспортным компаниям исследуется зависимость годового дохода (переменная Y, млн

Пример 1

По 12 транспортным компаниям исследуется зависимость годового дохода (переменная Y, млн. руб.) от среднегодового количества грузовых автомобилей (переменная X). Имеются данные, для удобства упорядоченные по фактору X:

№ п/п	1	2	3	4	5	6	7	8	9	10	11	12
X	15	18	22	27	25	31	34	37	40	45	48	48
Y	235	250	247	287	260	262	307	280	357	410	389	311

Требуется:

1. Построить линейную модель парной регрессии Y по X.

2. Проверить наличие гетероскедастичности возмущений методом Голдфельда–Квандта.

3. При обнаружении гетероскедастичности возмущений построить взвешенную модель регрессии.

1. По исходным данным строим линейную модель парной регрессии

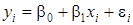(i =1, 2, …, n; n=12).

Параметры модели оцениваем обычным методом наименьших квадратов. С помощь табличного процессора MS Excel были определены коэффициенты уравнения регрессии 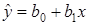: b₀=160,6; b₁=4,277. Таким образом, уравнение примет вид:

.

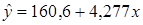Уравнение регрессии статистически значимо на уровне a=0,05: F‑статистика имеет значение F=25,15; табличное значение F-критерия Фишера — F_{0,05; 1;10}=4,96; коэффициент детерминации — R²=0,716.

Значение углового коэффициента уравнения регрессии b₁=4,277 показывает, что увеличение количества автомобилей на одну единицу приводит к росту годового дохода в среднем на 4,277 млн. руб.

Визуальный анализ графика зависимости годового дохода от количества автомобилей дает основание предполагать наличие гетероскедастичности возмущений. Видно, что отклонение от линии регрессии наблюдений, соответствующих крупным предприятиям, больше, чем для малых предприятий:

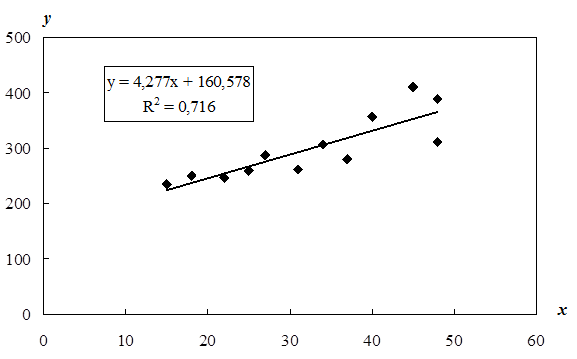
2. Построим график остатков и проведем его визуальный анализ. Предсказываемые уравнением регрессии значения результата 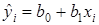и остатков 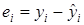(i =1, 2, …, n; n=12) приведены в таблице:

i	1	2	3	4	5	6	7	8	9	10	11	12
xi	15	18	22	27	25	31	34	37	40	45	48	48
yi	235	250	247	287	260	262	307	280	357	410	389	311
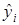
	225	238	255	276	268	293	306	319	332	353	366	366
ei	10	12	-8	11	-8	-31	1	-39	25	57	23	-55

График остатков по фактору X показан на рисунке:

Визуальный анализ графика остатков показывает, что их разброс растет по мере увеличения фактора Х, что может свидетельствовать о гетероскедастичности возмущений. Проверим это предположение методом Голдфельда–Квандта. Будет считать, что возмущения распределены по нормальному закону и их среднее квадратическое отклонение пропорционально значению фактора Х. Все остатки уже упорядочены по Х. Выбираем 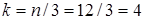первых и последних остатков. По каждой из групп определяем сумму квадратов остатков:

;

.

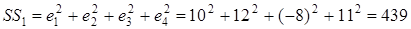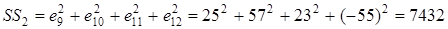Так как SS₂>SS₁, то F-статистику рассчитываем по формуле

.

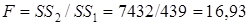Табличное значение F-критерия Фишера для уровня значимости a=0,05 и чисел степеней свободы числителя и знаменателя 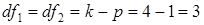(где p=1 — число факторов в модели) составляет F_{0,05; 3;3}=9,28.

Так как 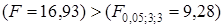, статистическая гипотеза об одинаковой дисперсии возмущений отклоняется на уровне значимости a=0,05. Факт наличия гетероскедастичности возмущений считается установленным.

3. Применим взвешенный МНК к исходной модели в предположении, что среднее квадратическое отклонение возмущений пропорционально значению фактора Х, для чего масштабируем исходные данные по Х:

i	1	2	3	4	5	6	7	8	9	10	11	12
1/xi	0,0667	0,0556	0,0455	0,0370	0,0400	0,0323	0,0294	0,0270	0,0250	0,0222	0,0208	0,0208
yi/xi	15,67	13,89	11,23	10,63	10,40	8,45	9,03	7,57	8,93	9,11	8,10	6,48

Исходную модель преобразуем в модель 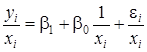(i =1, 2, …, n; n=12). Оцениваем параметры преобразованной модели b₁ и b₀ обычным методом наименьших квадратов. С помощь MS Excel были определены коэффициенты уравнения регрессии 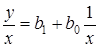преобразованной модели: b₁=3,863; b₀=173,2, и уравнение регрессии примет вид:

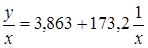(F=106; R²= 0,914).

Угловой коэффициент данного уравнения сравнивают со свободным членом исходного уравнения регрессии и наоборот. Видно, что значения соответствующих параметров уравнений отличаются друг от друга.

Тест Голдфельда–Квандта, примененный к преобразованной модели, не выявляет гетероскедастичности ее возмущений: F-статистика 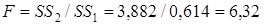не превышает табличное значение F-критерия Фишера .

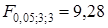Используя преобразованное уравнение регрессии делаем вывод, что увеличение количества автомобилей на одну штуку приводит к росту годового дохода в среднем на 3,863 млн. руб.

Дата добавления: 2014-01-05