Теория устойчивости лиофобных золей - теория ДЛФО

(физическая теория)

(качественное рассмотрение, без количественных выкладок)

Современная теория устойчивости, развитая советскими учеными Дерягиным и Ландау, получила всеобщее признание. Несколько позже теоретическая разработка, почти аналогичная и приводящая к тем же результатам, была осуществлена независимым путем голландскими учеными Фервеем и Овербеком. Поэтому современная теория устойчивости носит имя указанных ученых и известна в литературе как теория ДЛФО (DLVO).

Основная идея теории: Процесс коагуляции рассматривается как результат совместного действия двух родов сил:

1) электростатических сил отталкивания между частицами с энергией U_отт > 0;

2)вандерваальсовых сил притяжения между частицами с энергией U_пр < 0.

Результирующая энергия межчастичного взаимодействия (U) определяется как сумма двух составляющих:

U = U_отт + (-U_пр) = U_отт - U_пр

Если |U_отт| > |U_пр |, то преобладают силы отталкивания между частицами, коагуляция не происходит и золь является агрегативно устойчивым.

Если |U_отт| < |U_пр |, то преобладают силы притяжения между частицами, происходит коагуляция.

Рассмотрим подробнее количественную интерпретацию этих сил.

Электростатические силы отталкивания

Электростатические силы отталкивания возникают между мицеллами при перекрывании диффузных слоев противоионов, они стремятся оттолкнуть частицы друг от друга. Энергия этих сил:

U_отт = А е^-ch

где h - расстояние между взаимодействующими частицами;

c - 1/d величина обратная величине диффузионного слоя мицеллы (d);

А - величина, которая не зависит от “ h ”, она определяется параметрами ДЭС.

Величина c и А могут быть рассчитаны на основе теории ДЭС.

Расчеты U_отт показывают, что энергия отталкивания уменьшается:

- при увеличении заряда противоиона и его концентрации;

- при уменьшении по абсолютной величине j₀ и дзета - потенциала.

U_отт убывает с увеличением расстояния между частицами (h) по экспоненциальному закону (“ h ” входит как степень экспоненты: е^-ch).

Вандерваальсовы силы притяжения

Межмолекулярные силы притяжения основаны, главным образом, на дисперсионных взаимодействиях между молекулами. Они рассчитываются по уравнению:

U_пр = -А_г / 48 p h²,

где А_г - константа молекулярных сил, назваемая константой Гамакера.

Константа А_г» 10^-12 эрг и вычисляют ее квантово - статистическим путем. Она слагается из отдельных констант, характеризующих когезионные* и адгезионные** взаимодействия.

U_пр изменяется с увеличением расстояния между частицами (h) обратно пропорционально квадрату расстояния. Таким образом притяжение сравнительно медленно ослабевает с расстоянием. Так, при увеличении h в 100 раз, U_пр уменьшается в 10⁴ раз, а U_отт в 10⁴³ раз.

Результирующая энергия взаимодействия между частицами, находящимися на расстоянии “ h ”, определяется уравнением:

U(h) = A e^{- ch} - A_г / 48 p h²

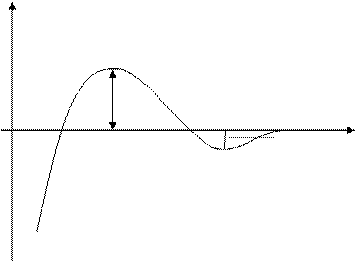
Так как характер зависимости от h для энергии притяжения и энергии отталкивания различный, надо полагать, что зависимость суммарной потенциальной энергии межчастичного взаимодействия от расстояния между частицами будет иметь сложный немонотонный характер. Общий вид этой зависимости [U(h)] можно представить графиком:

Энергия отталкивания	U     II DUk h1 h2 hmin h3
Энергия притяжения	hmax DUпр h III I

Рис.12.1. Потенциальная кривая взаимодействия двух частиц дисперсной фазы.

На этой кривой можно выделить три участка:

I участок: 0 < h < h₁, U(h) < 0 - между частицами преобладают силы притяжения, наблюдается ближний минимум: U_отт ® const; U_пр® - ¥. Частицы слипаются, происходит коагуляция.

II участок: h₁ < h < h₂, U(h) > 0 - между частицами преобладают силы отталкивания. U_отт > |U_пр |.

III участок: h₂ < h < h₃, U(h) < 0 - обнаруживается дальний минимум, однако глубина его невелика.

При h = h₁, h₂ и h₃ U(h) = 0, т.е. на этих расстояниях между частицами силы притяжения уравновешиваются силами оттлакивания.

Следовательно, если частицы сблизятся до расстояния меньше h₁, то они неизбежно слипнутся, но для этого им нужно преодолеть потенциальный барьер (DU_к). Смогут ли они это сделать зависит от величины потенциального барьера коагуляции и от кинетической энергии коллоидных частиц, которая среднестатистически близка произведению “kT”.

Потенциальную кривую взаимодействия двух частиц, представленную на рисунке 12.1. можно интерпретировать с помощью шарика и поверхности стола, изображенных на рис.12.2.

DU_k

DU_min

Рис.12.2. Интерпретация потенциальной кривой взаимодействия двух частиц.

Стол имеет высокий край и вблизи этого края находится ямка. По столу катится шарик, что с ним может произойти?

Если шарик катится медленно (т.е. кинетическая энергия его мала) то он, попав в ямку на поверхности стола, в ней и останется.

Если шарик катится быстро и способен выбраться из ямки, но не способен преодолеть высокий край стола, то ударившись в него, он откатится назад.

Если шарик катится очень быстро, то он способен не только выскочить из ямки, но и перескочить через высокий край стола и упасть на пол (это аналогично тому, чтобы слипнуться с другой частицей).

Аналогично происходит взаимодействие между частицами. Будем одну частицу считать неподвижной, а вторую приближающейся к ней с энергией “ kT ”.

Если kT < D U_min, то частицы остануться на расстоянии h_min и будут связаны друг с другом через слой дисперсионной среды, т.е. образуют “пару”, но непосредственно друг с другом не слипаются и не теряют своей седиментационной устойчивости. Говорят, что взаимодействие произошло в дальнем минимуме.

Если D U_min < kT << D U_к, то частицы при столкновении “отлетают” друг от друга, Z_эф = 0, u_к = 0. Система агрегативно устойчива.

Если kT < D U_к, то происходит медленная коагуляция.

Если kT > D U_к, то происходит быстрая коагуляция, Z_эф = 1, u_к = const. Так как золь обычно рассматривается при постоянной температуре, то кинетическая энергия частиц тоже остается постоянной. Следовательно, для коагуляции надо уменьшить потенциальный барьер коагуляции (D U_к). Как это сделать?

Чаще всего это делается с помощью добавления электролита – коагулянта, теория ДЛФО дает возможность вычислить порог быстрой коагуляции (С_кб):

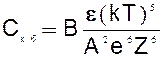
где А,В - постоянные величины, могут быть рассчитаны;

e - диэлектрическая проницаемость среды;

Z - заряд иона - коагулянта;

е - заряд электрона;

k - постоянная Больцмана (R/N_A);

Т - температура.

Из этой формулы видно, что зависимость С_кб от заряда иона - коагулянта такая же, как установлена эмпирическим правилом Шульце - Гарди:

С_кб = В (1/ Z⁶)

Дата добавления: 2014-01-05