Универсальная теория Мора

Пятая теория прочности – теория предельных состояний (теория Мора).

Критерий равнопрочности: напряженные состояния равнопрочны по наступлению предельного состояния, если при одновременном пропорциональном увеличении главных напряжений их круги Мора одновременно коснутся предельной огибающей.

Если изобразить в координатах t-s семейство кругов Мора для различных предельных состояний материала, то огибающая этого семейства будет предельной огибающей для данного материала.

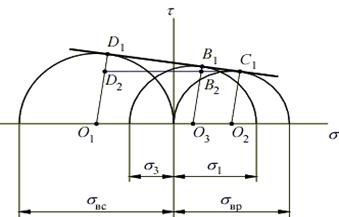
Изобразим в координатах t-s три предельных круга Мора:

- круг с центром в точке O ₁ – для случая одноосного сжатия (главные напряжения σ ₁ = 0, σ ₂ = 0, σ₃ = σ _вс);

- круг с центром в точке O ₂ – для случая одноосного растяжения (главные напряжения σ ₁ = σ _вр, σ ₂ = 0, σ₃ = 0);

- круг с центром в точке O ₃ – для случая плоского напряженного состояния (главные напряжения σ ₁, σ₃).

Линия C ₁ D ₁, огибающая круги, называется предельной огибающей.

Как видно из рисунка, , то есть

.

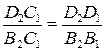Запишем длины отрезков через соответствующие напряжения:

,

,

,

.

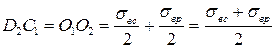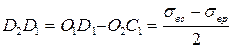Подставляя эти значения в пропорцию, получим

,

откуда:

.

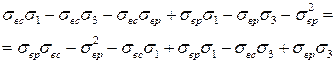После сокращения имеем

,

тогда

, где .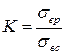

Т.к. 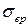– предел прочности для одноосного растяжения, его можно заменить .

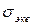Таким образом, эквивалентное напряжение по теории Мора, равно:

.

Для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию, 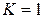, следовательно

,

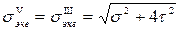то есть теория Мора совпадает с теорией максимальных касательных напряжений.

Для хрупких материалов , и

.

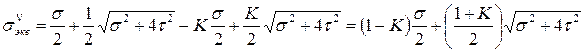Интересно, что для весьма хрупких материалов с

,

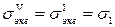то есть теория Мора совпадает с теорией максимальных нормальных напряжений.

Теорию Мора рекомендуется использовать для хрупких (в том числе анизотропных) материалов вместо первой и второй теорий. Ее недостатком является неучет промежуточного главного напряжения σ₂.

Дата добавления: 2014-01-05