Пределы применимости формулы Эйлера. Формула Ясинского

Формула Эйлера справедлива, если выполняется закон Гука, то есть критическое напряжение не превышает предела пропорциональности материала: , откуда

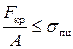, или .

Используя понятие радиуса инерции , запишем

.

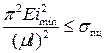Обозначим – гибкость стержня. Тогда условие применимости формулы Эйлера примет вид:

.

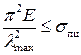Из предельного случая: , можно определить предельное значение гибкости

,

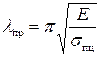которое, как видно из формулы, зависит только от свойств материала стержня. Например, для стали Ст3 l _пр»100.

Для случая, когда стержень теряет устойчивость за пределами выполнимости закона Гука, зависимость напряжений и деформаций принимает дифференциальную форму и получить аналитическое выражение для определения критических параметров стержня достаточно сложно.

Русский ученый Ф.С.Ясинский на основе многочисленных экспериментальных исследований предложил эмпирические формулы для вычисления критических напряжений при 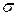_крпц:

– для сталей,

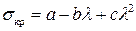– для чугунов,

где a, b, c – эмпирические коэффициенты, зависящие от марки материала и имеющие размерность напряжения (определяются по таблицам).

Для пластичного материала зависимость критического напряжения от гибкости стержня имеет вид:

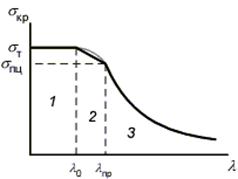
1 – зона малой гибкости;

2 – зона средней гибкости (зона Ясинского);

3 – зона большой гибкости (зона Эйлера).

В области большой гибкости (при 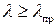) критическое напряжение определяется по формуле Эйлера

.

В области средней гибкости (при 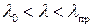) критическое напряжение определяется по формулам Ясинского. Величину l ₀ можно определить из условия

.

В области малой гибкости (при ) расчет на устойчивость производить не имеет смысла.

Дата добавления: 2014-01-05