Силовой расчет групп Ассура

Лекция 6

Силовой расчет группы Ассура 2 класса 1 вида.

Изобразим в масштабе группу Ассура 2-го класса 1-го вида (рис. 25) и приложим к звеньям группы все силы и моменты пар сил, активные и инерции.

Рис. 25 Группы Ассура 2-го класса 1-го вида с приложенными силами и моментами пар сил.

При этом все силы, действующие на звено, приведем к одной силе, все моменты пар сил – к одному моменту.

Примем следующие обозначения. Звено, к которому присоединяется звено AB обозначим номером 1, звено AB – номером 2, звено BС – номером 3, звено, присоединенное к BС – номером 4. Силы и моменты пар сил имеют индексы номеров звеньев, к которым они приложены. Силы взаимодействия звеньев будем обозначать двумя цифрами, разделенными чертой. Первая цифра обозначает номер звена, которая действует на звено, номер которого соответствует второй цифре, например: F _1-2 – сила действия 1-го звена на 2-е.

Пусть звенья группы Ассура 2-го класса 1-го вида нагружены силами F ₂ и F ₃ и моментами M ₂ и M ₃. Требуется определить давления в кинематических парах A, B и C, т.е. F _1-2, F _2-3, F _4-3, которые являются силами взаимодействия звеньев. Эта задача решается методом планов сил. Для этого записываем уравнение равновесия группы ABC в векторной форме, приравняв к нулю сумму всех действующих на нее сил.

(10)

В уравнении (10) у сил F ₂ и F ₃ известны точки приложения, модули и направления, у сил F _1-2 и F _4-3 известны только точки приложения – в центре шарниров A и C. Для определения величин этих сил раскладываем каждую из них на две составляющие: нормальную , направленную вдоль звена и касательную 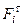, направленную перпендикулярно звену.

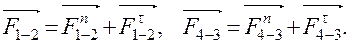(11)

Определим составляющие 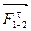и 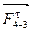из уравнения равновесия звеньев 2 и 3, рассмотренных по отдельности. Из условия равновесия звена 2

(12)

В уравнении (12) сумма моментов принимается алгебраической, как и в последующих уравнениях. Определим величину составляющей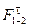

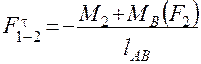
где	MB(F 2 )	–	момент силы F 2 относительно точки B;
lAB	–	длина звена AB.

Если после определения 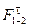она окажется отрицательной, то ее истинное направление должно быть выбрано противоположным.

Аналогичным образом определяем величину составляющей , рассматривая равновесие звена B_l

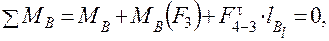
Запишем уравнение равновесия все группы Ассура в векторной форме

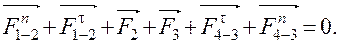(13)

При графическом решении уравнения равновесия силовой многоугольник должен быть замкнутым. Строим силовой многоугольник в соответствии с уравнением (13). Из произвольной точки k отложим вектор 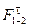, затем последовательно суммируем силы 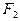, , . Все векторы строим в масштабе сил 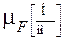. Замкнем силовой многоугольник следующим образом. Из конца вектора проведем прямую по направлению , а из точки k – прямую по направлению Fⁿ. В точке пересечения этих прямых будут находиться конец вектора и начало вектора . Векторы 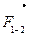и получаем в соответствии с уравнениями (11). План сил группы приведен на рис..25 а.

Рис. 25 а План сил группы Ассура 2 класса 1 вида

Для определения реакции в кинематической паре B рассмотрим равновесие 2-го, либо 3-го звена. Для звена AB

(14)

В векторном уравнении (14) неизвестная сила F _3-2 – сила действия третьего звена на второе AB. Строим это уравнение, используя уже построенный план сил, на котором векторы F _1-2 и F ₂ проведены. Для определения F _3-2 необходимо замкнуть силовой треугольник в соответствии с уравнением.(14), т.е. соединить конец вектора F ₂ с началом вектора F _1-2.

Силовой расчет группы Ассура 2 класса 2 вида.

Группа второго вида имеет одну внешнюю поступательную пару C с осью x-x (рис. 26). На звенья группы действуют силы F ₂ и F ₃, а также пары сил с моментами M ₂ и M ₃. Требуется определить F _1-2 (давление в паре A), F _3-2 (давление в паре B), F _0-3 (силу давления направляющей на ползун) и плечо силы F _0-3 относительно точки B. Давления в кинематических парах определим при помощи плана сил. Уравнение равновесия сил, действующих на группу, в векторной форме, запишем в виде

(15)

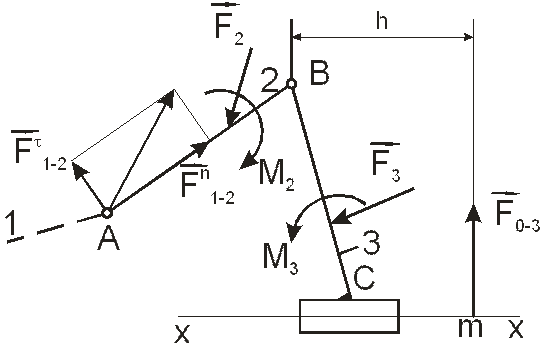
Рис. 26 Группа Ассура 2-го класса 2-го вида с приложенными силами и моментами пар сил

Рис. 27 План сил группы Ассура 2-го класса 2-го вида

Для реакции 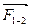известна точка ее приложения, неизвестными являются направление и величина. Реакция 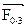, т.е. сила давления направляющей на ползун, известна по направлению: она перпендикулярна к оси x-x направляющей. Неизвестными являются точка ее приложения и величина.

Разложим силу на две составляющие – нормальную по направлению оси звена AB и касательную 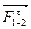, направленную по нормали к оси. Таким образом

.

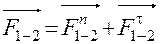Величину составляющей 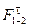определим из условия равновесия звена AB, которое запишем в виде суммы моментов всех сил относительно точки B и приравняем к нулю

,

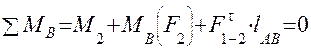откуда

.

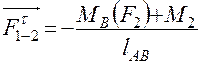Подставим в векторное уравнение (15) вместо силы F _1-2 сумму составляющих

.

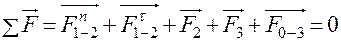В этом уравнении неизвестны по величине, но известны по направлению силы 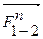и . Построим план сил, для чего из произвольной точки k (рис. 27) откладываем в выбранном масштабе сил μ _F вектор 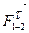, к нему последовательно прибавляем силы 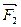и 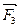в том же масштабе. Замыкаем силовой многоугольник следующим образом. Из конца вектора 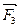проводим линию, перпендикулярную оси направляющей x-x, а из начала вектора 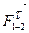(точки k) – линию, параллельную оси звена AB. На пересечении этих линий получаем точку, которая является концом вектора 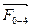и одновременно началом вектора 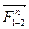. 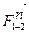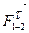Геометрическая сумма векторов и определит в масштабе μ _F вектор силы.

Реакцию в паре B определим из условия равновесия сил звена AB, которые запишем в векторной форме

.

Таким образом, для определения достаточно соединить на имеющемся плане сил конец вектора 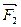с началом вектора.

Эту же реакцию, как силу действия звена 2 на звено 3 можно определить, рассмотрев равновесие звена BC.

.

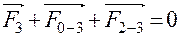Для определения достаточно соединить конец вектора с началом вектора 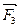. Вектора и в силу закона равенства действия и противодействия равны по величине и направлены в противоположные стороны.

Плечо силы относительно точки B (положение точки m на направляющей x-x) определим из условия равновесия звена BC, приравняв к нулю сумму моментов всех сил, действующих на это звено, относительно точки B.

(16)

Уравнение записано в алгебраическом виде. Если при численных расчетах величина h получится отрицательной, то силу следует расположить на расстоянии h по другую сторону от точки B.

При решении задач может оказаться, что при расчетной величине плеча h точка приложения m силы находится за пределами реальных геометрических размеров ползуна. Установим, каким образом эта сила воспринимается звеньями пары. Обозначим плечо силы относительно центра ползуна h', а длину ползуна – l (рис. 28)

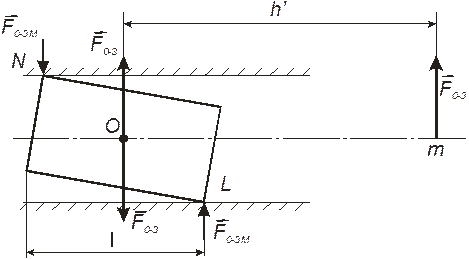
Рис. 28 Распределение реакции по направляющей

поступательной пары

Приложим в центре ползуна уравновешенную систему двух сил . В.результате получим, что на ползун действует сила , приложенная в центре O и пара сил с моментом M, равным по величине

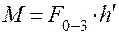
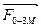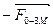Пару сил с моментом M удобнее представлять в виде двух сил и , приложенных в крайних точках ползуна N и L. Величина силы 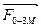равна

.

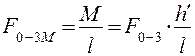Дата добавления: 2014-01-05