Пример силового расчета механизма

Лекция 7

Для шестизвенного шарнирного механизма (рис. 30) дано: размеры звеньев, закон движения ведущего звена OA, положения центров тяжести звеньев. Массы звеньев m ₂=10кг, m ₃=15кг, m ₄=10кг, m ₅=20кг. Моменты инерции звеньев относительно центральной оси 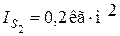, , 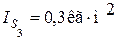. Сила полезного сопротивления F ₅=300Н. Массой кривошипа пренебречь ввиду малой величины.

Для данного положения механизма построен план ускорений и определены ускорения центров тяжести звеньев и их угловые ускорения. Ведущее звено приводится в движение через пару прямозубых цилиндрических зубчатых колес с числом зубов z ₁=60, z ₂=150; модуль зацепления m =2 мм.

Требуется определить внутренние силы в шарнирах и уравновешенную силу F_y.

Решение. Определим силы тяжести звеньев.

Определим силы инерции и момент пар сил инерции звеньев.

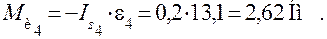
Силы инерции прикладываем в точках центров тяжести, направляя их противоположно направлениям ускорений этих точек, а моменты инерции – противоположно угловым ускорениям.

Рис. 30 Кинематическая схема шестизвенного механизма. μ _S =0,01 м/мм.

Рис. 31 План ускорений механизма μ _a =0,156 м/с² ·мм.

Разберем механизм на группы Ассура и начинаем проводить силовой расчет диады 2-го вида CE, наиболее удаленной от ведущего звена. В шарнире C прикладываем нормальную и касательную составляющие усилия, действующего со стороны звена DBC. К ползуну, по его центру прикладываем реакцию направляющей F _0-5 (рис. 32)

Рис. 32 Силовой расчет диады CE. μ _S =0,01 м/мм.

В начале определим составляющую из условия равновесия, записанного в виде уравнения моментов всех сил, действующих на звено CE, относительно точки E:

(17)

Так как группа изображена в масштабе μ _S =0,01 м/мм, то плечи сил h₁ и h₂, замеренные на чертеже, необходимо умножить на этот масштаб, либо привести к масштабу чертежа момент M _и4, поделив его на масштаб μ _S. Решаем уравнение (17) относительно :

.

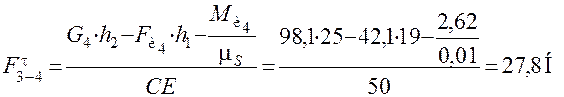В результате решение уравнения сила получилась со знаком плюс, что означает правильный выбор ее направления на схеме силового расчета. Если сила получится со знаком минус, то в силовом многоугольнике ее необходимо направлять в противоположную сторону.

Для определения величин двух оставшихся неизвестных сил и F _0-5 составим уравнение равновесия всей группы Ассура в векторной форме:

В соответствии с этим уравнением строим замкнутый силовой многоугольник, начиная с известных сил и заканчивая построение двумя неизвестными по величине, но известными по направлению силами и F _0-5.

Выбираем для построения масштаб сил μ _F =6 Н/мм. Определим длину отрезков, которые в плане сил будут изображать эти силы.

Сложив все известные силы, из конца вектора (точка k) проводим направление силы , а из начала вектора (точка a) проводим направление силы 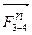. Точка пересечения h является концом вектора и началом 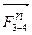(рис..33)

Рис. 33 План сил диады CE. μ _F =6 Н/мм.

Просуммировав вектора и определим силу F _3-4 действия звена 3 на звено 4. Величина этой силы равна произведению отрезка hb на масштаб μ _F.

F _3-4= hb ·μ _F =69·6=414 Н

Для упрощения расчетов считаем известной точку приложения реакции F _0-5, линия ее действия проходит через центр шарнира E. Силу давления направляющей на ползун определим, помножив отрезок kh на масштаб сил.

F _0-5= kh ·μ _F =70·6=420 Н.

Давление в шарнире E определим, рассмотрев равновесие шатуна CE, либо ползуна E. Запишем векторное уравнение равновесия ползуна:

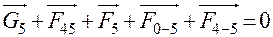(18)

Неизвестную силу F _4-5 действия шарнира на ползун определяем замыкая силовой многоугольник в соответствии с уравнением для чего конец вектора F _0-5 соединяем с началом вектора G ₅ (линия hd). Величина этой силы

F _4-5= hd ·μ _F =71·6=426 Н.

Переходим к силовому расчету следующей группы Ассура, состоящей из звеньев 2 и 3 (рис. 34). Разрушаем шарнир A и прикладываем касательную и нормальную составляющие силы, действующей на звено AB со стороны кривошипа. В точке D прикладываем касательную 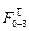и нормальную составляющие реакции, действующей на звено DB_l со стороны стойки. Кроме этих сил в точке C прикладываем силу F _4-3 – силу давления звена 4 на звено 3. Она равна по величине силе F _3-4, но направлена в противоположную сторону.

Рис. 34 Силовой расчет диады ABD. μ _S =0,01 м/мм.

Определим силу F _1-2 из условия равновесия звена AB, для чего запишем уравнение моментов всех сил, действующих на звено 2 относительно точки B:

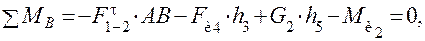
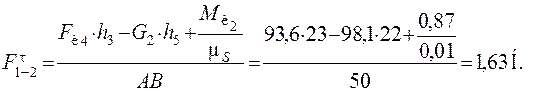
Определим силу 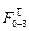, рассмотрев равновесие звена 3. Для этого также запишем уравнение моментов всех сил, действующих на звено 3 относительно внутренней пары группы Ассура – точки B.

После определения и 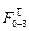строим силовой многоугольник в соответствии с векторным уравнением равновесия всей группы

.

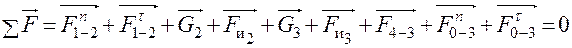Примем тот же масштаб сил μ _F =6 Н/мм, что и для предыдущей группы (4,5). Определим длину отрезков, изображающих векторы сил в масштабе:

Построение начинается со сложения известных сил. Из конца вектора проводим прямую, параллельную , через начало вектора проводим линию по направлению силы . Точка пересечения h является началом вектора и одновременно концом вектора (рис. 35).

Геометрическая сумма векторов и (прямая к h) представляет в масштабе μ _F силу реакции стойки.

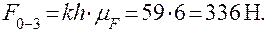
Рис. 35 План сил диады ABD. μ _F =6 Н/мм.

Сила взаимодействия кривошипа OA с шатуном AB определится как геометрическая сумма нормальной и тангенциальной составляющей реакции 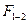. На плане сил этот вектор представлен линией hb.

Давление во вращательной паре B можно найти рассмотрев равновесие 2 либо 3 звена. Запишем уравнение равновесия звена 3 в векторной форме.

.

Для того, чтобы силовой многоугольник был замкнут, достаточно соединить конец вектора F _0-3 с началом вектора G ₃. Сила давления звена 2 на звено 3, то есть давление в паре В представлено в плане сил прямой линией hd. Величина этой силы:

Заканчиваем силовой расчет ведущим звеном. Определяем диаметры делительных окружностей шестерни и колеса:

Палец шарнира A расположен на зубчатом колесе. Строим в масштабе μ _S расчетную схему ведущего звена, в полюсе зацепления P прикладываем уравновешивающую силу F_y, как это было рассмотрено ранее. К концу кривошипа прикладываем силу F _2-1, которая равна определенной из предыдущего расчета силе F _1-2 и направлена в противоположную сторону (рис. 36).

Рис. 36 Силовой расчет ведущего звена. μ _S =0,005 Н/мм.

Величину уравновешивающей силы определим из условия равновесия ведущего звена:

Давление в шарнире O определим, построив силовой треугольник в соответствии с уравнением равновесия ведущего звена в векторной форме

Реакция стойки определяется вектором ca, соединяющим конец вектора F _2-1 с началом вектора F_y (рис. 37). Для построения силового треугольника определим длины отрезков, изображающие векторы сил в масштабе μ _F =6 Н/мм.

Рис. 37 План сил ведущего звена. μ F =6 Н/мм.

Величина реакции стойки F _0-1= ca ·μ_F=50·6=300 Н.

Дата добавления: 2014-01-05