Методы нулевого порядка

Оценка эффективности методов оптимизации

Большое разнообразие итерационных алгоритмов ставит перед пользователем задачу выбора. Для этого следует выставить критерии, на основании которых один алгоритм будет считаться более предпочтительным, нежели другой. С этой целью обычно используют следующие оценки:

1. Точность поиска – значение окрестности локального оптимума, в которую приводит алгоритм после выполнения заданного числа итераций.

2. Скорость сходимости – число итераций, необходимое для достижения заданной точности.

3. Время счета – время поиска на ЭВМ локального оптимума с заданной точностью, отнесенное к коэффициенту сложности задачи (или к быстродействию ЭВМ).

4. Стабильность – свойство алгоритма незначительно увеличивать число итераций при малых возмущениях выбора начальных точек, а также вследствие погрешности вычислений.

5. Надежность − свойство алгоритма приводить к оптимуму при многократном повторении поиска из разных начальных точек.

Для сравнения алгоритмов по этим критериям следует производить расчеты в одинаковых или близких условиях. Оценка алгоритма по скорости сходимости в некотором смысле обратна оценке их точности. Задание высокой точности может существенно увеличить число итераций метода оптимизации. Необоснованное снижение точности может нарушать теоретические предположения, положенные в основу задачи (например, условие ортогональности в методе сопряженных градиентов нарушается при низкой точности выбранного метода одномерной минимизации).

Классификация методов безусловной оптимизации

В зависимости от наивысшего порядка частных производных целевой функции, используемых для формирования итерационного процесса численные методы безусловной минимизации принято делить на три группы:

· Методы нулевого порядка или прямого поиска. Одномерная минимизация – метод деления отрезка пополам, метод дихотомии, метод золотого сечения, метод Фибоначчи и др. Многомерная оптимизация – метод конфигураций (Хука-Дживса), метод Розенброка, метод сопряженных направлений и др.

· Методы первого порядка – методы градиентного спуска (с постоянным шагом, наискорейшего спуска), метод покоординатного спуска, метод Гаусса- Зейделя и др.

· Методы второго порядка – метод Ньютона, метод Ньютона-Рафсона и др.

1. Виды

– методы случайного поиска. Основаны на последовательной случайной генерации достаточно большого количества значений в промежутке нахождения корня с последующим сужением этого промежутка

Стратегия поиска

1. На промежутке 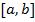с помощью генератора случайных чисел образуется массив из значений независимой переменной и функции ().

2. Среди элементов массива значений функции находится оптимальное значение (), а также соответствующее ему значение переменной ().

3. Рассчитывается новый промежуток, в пределах которого будет производиться последующий выбор из N значений

Используется для задач большой размерности. Особенно эффективен для овражных функций.

– методы исключения интервалов (правило Свенна)

Стратегия поиска

1. Выбор начального интервала неопределенности (интервал, на котором функция унимодальна – достигает глобального минимума на интервале в единственной точке)

2. Уменьшение интервала неопределенности

3. Поиск заканчивается, когда интервал неопределенности меньше установленной величины

– методы полиномиальной аппроксимации

Согласно теореме Вейерштрасса об аппроксимации, непрерывную функцию в некотором интервале можно аппроксимировать степенным полиномом достаточно высокого порядка. Следовательно, если функция унимодальна и найден полином, который достаточно точно ее аппроксимирует, то координаты точки оптимума функции можно оценить путем вычисления координаты точки оптимума полинома.

2. Методы одномерной минимизации

1. Метод равномерного поиска. Отрезок делится на равных частей и находится точка 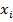, в которой значение функции наименьшее

2. Метод деления интервала пополам. На каждой итерации исключается половина интервала неопределенности

3. Метод дихотомии. Интервал неопределенности делится пополам и в обе стороны от середины откладывается по .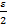

4. Метод золотого сечения. Точка производит «золотое сечение» отрезка, если отношение длины всего отрезка к большей части, равно отношению большей части к меньшей ().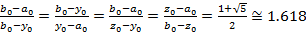

Алгоритм: 0 – положить , , 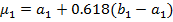вычислить . Положить k =1.

1 – если , то остановиться. Если , то перейти к 2, если , то к 3.

2 – положить 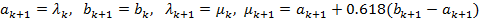. Вычислить и перейти к 4.

3 − положить 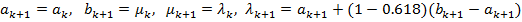. Вычислить и перейти к 4.

4 – заменить k на k+ 1 и перейти к 1.

5. Метод Фибоначчи. Числа Фибоначчи: Последовательность имеет вид 1, 1, 2, 3, 5, 8, 13, 21, …

Задается начальный интервал неопределенности длины 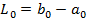и допустимая длина конечного интервала l. Находится количество вычислений N: .

,

,

.

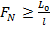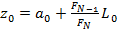
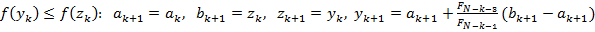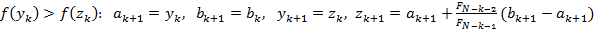6. Метод квадратичной интерполяции (метод Пауэлла). Задается начальная точка и с помощью пробного шага находятся три точки как можно ближе к точке минимума. В полученных точках вычисляются значения функции. Строится интерполяционный полином второй степени, проходящий через три точки. В качестве приближения точки минимума берется точка минимума полинома.

7. Сравнение по скорости сокращение интервала неопределенности. Пусть длина исходного интервала равна , а 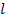– длина конечного интервала неопределенности. При заданной величине интервала 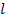, которая удовлетворяет требуемой степени точности, необходимое число вычислений функции n может быть определено, как наименьшее положительное целое, удовлетворяющее следующим соотношениям:

· метод дихотомии: ;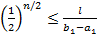

· метод золотого сечения: ;

· метод Фибоначчи: .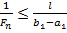

Для фиксированного значения наименьшее число вычислений целевой функции отвечает более эффективному алгоритму. С этой точки зрения наиболее эффективным является метод Фибоначчи, далее – метод золотого сечения, затем – метод дихотомии. При достаточно больших n значение , поэтому методы Фибоначчи и золотого сечения асимптотически эквивалентны.

3. Методы многомерной минимизации

1. Метод покоординатного спуска (Гаусса-Зейделя). Данный метод просто последовательно проводит одномерную оптимизацию по каждой координате функции. данный алгоритм эффективен в тех случаях, когда целевая функция является сепарабельной, т.е. может быть представлена в виде суммы функций, зависящих только от одной координаты.

Достоинство – простота, невысокие требования к памяти, сходимость практически с любых начальных приближений (кроме овражных функций – исправлено в методе Розенброка).

Основной недостаток – медленная сходимость. Методом покоординатного спуска задача минимизации сепарабельной функции будет решена за n (число координат) шагов, для функции общего вида – процесс бесконечный.

2. Метод конфигураций (метод Хука Дживса). Исследующий поиск + поиск по образцу. В качестве множества направлений выбирается множество координатных направлений. Фиксируется первое координатное направление и делается шаг в сторону уменьшения функции. После перебора всех координат исследующий поиск завершается. Полученная точка – новый базис. Если исследующий поиск с данной величиной шага неудачен, то шаг уменьшается. Поиск заканчивается, когда текущая величина шага станет меньше некоторой величины.

Поиск по образцу заключается в движении по направлению от старого базиса к новому. Если значение в наилучшей точке меньше, чем в предыдущей, то поиск по образцу удачен, если нет, то продолжается исследующий поиск с меньшим шагом.

3. Метод деформируемого многогранника (метод Нелдера-Мида или симплексный метод). В основу положено построение последовательности систем n +1 точек, которые являются вершинами выпуклого многогранника. В организации алгоритма поиска используется важное свойство симплекса – против каждой вершины находится одна грань.

Точки системы на k +1 итерации совпадают с точками на k итерации, кроме одной, наихудшей, т.е. точки с максимальным значением. Эта точка заменяется на другую по специальным правилам: вершина получается симметричным отражением выбрасываемой величины относительно центра противоположной грани. В результате многогранники деформируются в зависимости от структуры линий уровня целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направления в изогнутых впадинах и сжимаясь в окрестности минимума. Построение последовательности многогранников заканчивается, когда значение функции в вершинах текущего многогранника отличаются от значения функции в центре тяжести системы не более чем на ε.

При выходе в район оптимума процесс обычно зацикливается, в этом случае нужно сжимать симплекс, откладывая вершину на грани на расстоянии вдвое меньше, чем необходимо. Процесс сжатия происходит многократно, до тех пор, пока размеры симплекса не будут меньше заданной величины. Недостаток – невозможность ускорения вдали от оптимума.

4. Метод Розенброка. Направлен на ликидацию одного из недостатков метода покоординатного спуска – высокую чувствительность к выбору системы координат. Метод сводится по сути к отысканию «удачной»системы координат путем поворота исходных осей координат. Итеративный поиск направления убывания функции с помощью изменяемых дискретных шагов вдоль линейно независимых ортогональных направлений. В случае удачного шага в исследуемом направлении его значение на следующей итерации увеличивается с помощью коэффициента растяжения, а в случае неудачи уменьшается за счет умножения на коэффициент сжатия, при этом направление поиска меняется на противоположное. Если по каждому направлению поиска имеет место неудача, то строится новое множество линейно независимых и ортогональных направлений, циклический поиск по отдельным направлениям продолжается. Новые направления поворачиваются по отношению к предыдущим так, что они оказываются вытянутыми вдоль оврага.

5. Метод сопряженных направлений (метод Пауэлла). Используется тот факт, что минимум квадратичной функции может быть найден не более чем за n (размерность пространства) шагов при условии, что поиск ведется вдоль сопряженных относительно матрицы Гессе направлений. Неквадратичные функции представляются в окрестности точки минимума своей квадратичной аппроксимацией.

Задается начальная точка и направления, совпадающие с координатными. Находится минимум функции при последовательном движении по n +1 направлениям с помощью одного из методов одномерной минимизации. Полученная точка минимума берется в качестве исходной для поиска по следующему направлению, направление 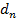используется как при первом, так и последнем поиске (). Находится новое направление поиска, сопряженное с 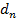. Оно проходит через точки, полученные при первом и последнем поиске. Повторяется поиск по n +1 направлениям, уже не содержащим направления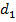

Дата добавления: 2014-01-05