Постановка задачи

Обоснование симплекс-метода (теорема существования решения) посм. у Васильева

Численные методы условной оптимизации: метод проекции градиента - Обоснование [2] метод проекции антиградиента

Линейное программирование – Васильев, matmet.pdf, посмотреть антициклины.

Безусловная оптимизация – проверочная остаточных знаний

Численные методы лекции по Васильеву

Ввести понятие унимодальности

4. 1 лекция – знакомство, литература, структура курса + классификация задач, балльно-рейтинговая система, лабораторные, условная оптимизация – метод Лагранжа (по Васильеву), многокритериальная оптимизация – на дом

6. Добавить доказательство в методе штрафов (Можно посмотреть Васильева или «штрафные функции.pdf)

8. Правило решения задач по симплекс-методу (попробовать переписать в терминах аij, bj - см. таблицы Пантелеева)

Конечномерные задачи без ограничений (задачи безусловной оптимизации)

Пусть , .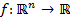

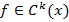Гладкой конечномерной экстремальной задачей без ограничений называется следующая задача:

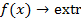
Точка 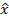является точкой локального минимума функции f, если существует окрестность 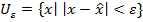точки 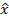такая, что 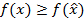для любой точки x из этой окрестности. При этом мы пишем .

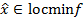Стационарная точка 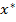функции 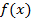называется регулярной, если в этой точке функция 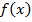дважды дифференцируема и определитель ее матрицы Гессе не равен нулю.

Правило решения экстремальной конечномерной задачи без ограничений (аналитическое решение):

1. Выписать необходимое условие экстремума I порядка – аналог теоремы Ферма:

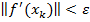(модуль градиента этого критерия)

(1) – недостаточна, т.к. функция может иметь поведение типа скачка (резкое изменение критерия оптимальности).

(2) – основана на предположении монотонного убывания величины 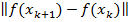в зависимости от числа итераций. При пологом характере 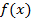вблизи оптимума, разность может мало меняться даже при большом шаге, поэтому (1)+(2).

(3) – характеризует скорость убывания критерия оптимальности и обращается в нуль в точке локального минимума. Поэтому по этой скорости можно судить о приближении к оптимуму.

Дата добавления: 2014-01-05