Методы второго порядка

Целевая функция должна быть дважды непрерывно дифференцируемой в 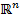. При помощи формулы Тейлора представим целевую функцию в окрестности точки 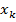в виде

Пренебрегая последним слагаемым в правой части, получаем квадратичную функцию

Если матрица Гессе 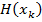целевой функции является положительно определенной, то точка 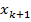минимума функции единственна и может быть найдена из условия, что ее градиент равен нулевому вектору:

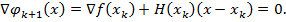
Отсюда получаем .

Если целевая функция является квадратичной вида где 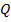– положительно определенная матрица порядка n, а – заданный вектор, то спуск из произвольной начальной точки в ньютоновском направлении приводит в точку минимума этой функции за одну итерацию. Для неквадратичной функции ньютоновское направление в общем случае не проходит через точку ее минимума, хотя часто оказывается к этой точке ближе, чем направление антиградиента. Если график целевой функции имеет овражную структуру, то вектор может составлять с осью оврага меньший угол, чем антиградиент. Эта особенность при минимизации таких функций делает алгоритмы метода Ньютона более эффективными, чем алгоритмы метода градиентного спуска.

1. Метод Ньютона. . Требование гарантированно выполняется при условии, что . Сходимость доказана только для класса выпуклых функций.

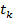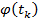2. Метод Ньютона-Рафсона. , где величина шага определяется из условия . Если функция достаточно сложна, то возможна ее замена полиномом 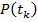. Окончание расчета: .

3. Метод Марквардта. , где как минимум на порядок больше, чем самый большой элемент матрицы 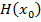. Если , то , в противном случае .

На начальных шагах метод ведет себя как метод первого порядка, в окрестности оптимума приближается к методам второго порядка. Для квадратичной функции значение оптимума можно получить за n (размерность задачи) шагов.

Конечномерные задачи с ограничениями (задачи условной оптимизации)

Дата добавления: 2014-01-05