Ограничения

Функция Лагранжа

Постановка задачи

Пусть , .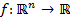

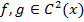Задачей условной оптимизации называется следующая задача:

,

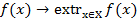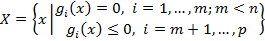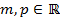, . (УО)

Обобщенная функция Лагранжа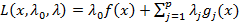

Классическая функция Лагранжа

Множители Лагранжа .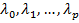

Градиент функции Лагранжа .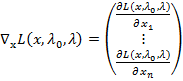

Второй дифференциал функции Лагранжа .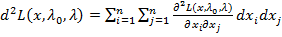

Первый дифференциал ограничения .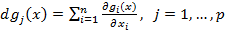

Ограничение 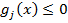называется активным в точке 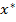, если 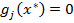. Если 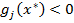, то ограничение называется пассивным.

Градиенты ограничений 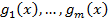являются линейно независимыми в точке 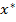, если равенство 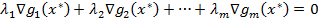выполняется только при 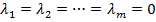, т.е. .

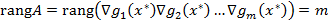В случае одного вектора: 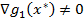− линейно независимая система, 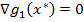– линейно зависимая.

Необходимые условия минимума (максимума) первого порядка

Пусть 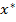- точка локального минимума (максимума) в задаче (УО). Тогда найдется такое число 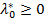и вектор 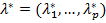, не равные одновременно нулю и такие, что выполняются следующие условия: (Н1)

· Условие стационарности функции Лагранжа по :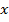

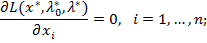
· Условие допустимости решения:

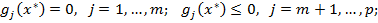
· Условие неотрицательности для условного минимума (неположительности для условного максимума):

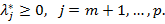
· Условие дополняющей нежесткости:

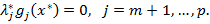
1. Если при этом градиенты активных ограничений-неравенств и ограничений-равенств в точке 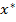линейно независимы (выполняется условие регулярности), то .

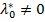2. При 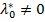: Если функции 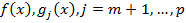выпуклые, а функции 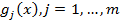линейные, то необходимые условия условного экстремума задачи (УО) являются одновременно и достаточными условиями глобального минимума. (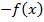выпуклая – глобального максимума). При этом множество допустимых решений X выпукло.

3. Из условия дополняющей нежесткости следует, что если ограничение-неравенство в точке 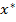пассивное, т.е. 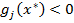, то 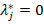, а если активное, т.е. 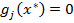, то 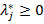для минимума и 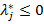для максимума.

Доказательство в случае ограничения типа равенства [1]

От противного: 1) Условие стационарности функции Лагранжа не выполняется, тогда система векторов 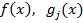линейно независима и ранг ее матрицы M отличен от нуля

2) Предполагается, что 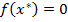, в противном случае – преобразование.

3) Рассматривается функция

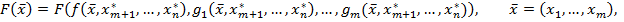
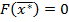, и 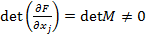. По теореме об обратной функции существует отображение 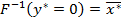и .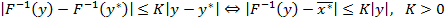

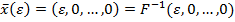В частности, для достаточно малого по модулю , определен вектор , для которого .

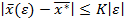Это означает, что 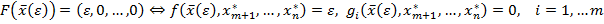и при этом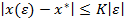

Получили, что в точке 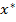функция f не достигает экстремума, так как в окрестности этой точки существуют точки 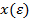, в которых функция принимает значения как больше, так и меньше .

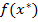Достаточные условия минимума (максимума) первого порядка

Пусть точка 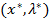удовлетворяет необходимым условиям минимума (максимума) первого порядка при 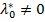, суммарное число активных ограничений-неравенств в точке 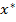и ограничений-равенств совпадает с числом n переменных, при этом выполняется условие регулярности (градиенты активных ограничений-неравенств и ограничений-равенств в точке 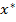линейно независимы). Если 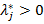для всех j, то 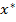− точка условного локального минимума задачи (УО). Если 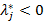для всех j, то 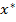− точка условного локального максимума задачи (УО).

Необходимые условия минимума (максимума) второго порядка

Пусть 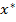− регулярная точка минимума (максимума) в задаче (УО) (в этой точке функция 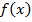дважды дифференцируема и определитель ее матрицы Гессе не равен нулю) и имеется решение 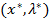системы (Н1). Тогда второй дифференциал классической функции Лагранжа, вычисленный в точке 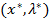, неотрицателен (неположителен):

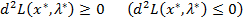
для всех 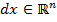таких, что

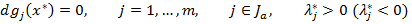
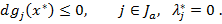
Дата добавления: 2014-01-05