Композиция двумерных преобразований

Понятие композиции было введено в предыдущем разделе. В данном разделе мы покажем, каким образом можно использовать композицию преобразований для объединения фундаментальных матриц R, S и Τ с целью получения желаемых общих результатов. Основное преимущество объединенных преобразований состоит в том, что к точке более эффективно применять одно результирующее преобразование, чем ряд преобразований друг за другом.

Рассмотрим, например, поворот объекта относительно некоторой произвольной точки Pi. Поскольку нам известно, лишь как поворачивать вокруг начала координат, разобьем исходную (трудную) проблему на три более легкие задачи. Таким образом, чтобы произвести поворот относительно точки Pi, необходимо выполнить последовательно три элементарных преобразования:

1. Перенос, при котором точка Pi перемещается в начало координат.

2. Поворот.

3. Перенос, при котором точка из начала координат возвращается в первоначальное положение Ρi.

Эта последовательность показана на рис. 2.3, на котором вокруг точки Ρi(x, у) поворачивается контур домика. Первый перенос производится на (-x₁, -y₁), в то время как последующий — на (x₁, y₁) — является обратным ему. Результат существенно отличается от того, который получился бы, если бы применялся один только поворот.

Результирующее преобразование имеет вид

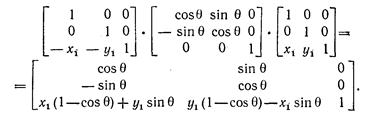
Эта композиция преобразований путем умножения матриц служит примером того, как применение однородных координат упрощает задачу.

Используя аналогичный подход, можно промасштабировать объект относительно произвольной точки Рi: перенести Ρi в начало координат, промасштабировать, перенести назад в точку Ρi. Результирующее преобразование в этом случае будет иметь вид

Предположим, что нам необходимо промасштабировать, повернуть и расположить в нужном месте домик, показанный на рис.2.3, где центром поворота и масштабирования является точка Ρ₁. Последовательность преобразований заключается в переносе точки Ρ₁ в начало координат, проведении масштабирования и поворота, а затем переносе из начала координат в новую позицию Р₂, в которой домик должен оказаться (эта последовательность показана на рис. 2.3). В структуре данных, в которой содержится это преобразование, могут находиться масштабный множитель (множители), угол поворота и величины переноса или может быть записана матрица результирующего преобразования:

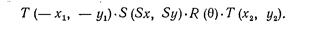
Если известно, что M₁ и M₂ представляют собой элементарные перенос, масштабирование или поворот, то при каких условиях Μ₁ и Μ₂ коммутативны? В общем случае умножение матриц некоммутативно. Однако легко показать, что в следующих частных случаях коммутативность имеет место (в этих случаях можно не беспокоиться о порядке перемножения матриц – см. Таблицу 2.1).

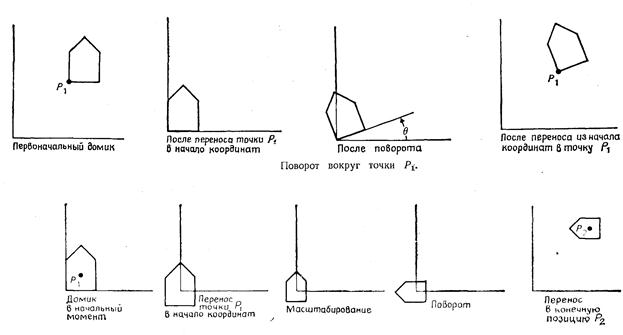
Рис. 2.3 Композиция преобразований

Таблица 2.1

M1	М2
Перенос	Перенос
Масштабирование	Масштабирование
Поворот	Поворот
Масштабирование (при Sx = Sy)	Поворот

Дата добавления: 2014-01-05