
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математика фракталов. Алгоритмы фрактального сжатия изображений
|
|
|
|
У фрактальной математики возникают все новые и новые сферы применения. Коснемся лишь одного перспективного направления — создания алгоритма фрактального сжатия графической информации. В 1991 году такой алгоритм был найден. Он имеет ряд уникальных возможностей. Фрактальный архиватор позволяет, например, при распаковке произвольно менять разрешение изображения без появления эффекта зернистости. Более того, он распаковывает гораздо быстрее, чем ближайший конкурент, JPEG, и не только статическую графику, но и видео. В 1992 году компания Microsoft использовала фрактальный архиватор и выпустила компакт-диск Microsoft Encarta мультимедиа-энциклопедия, содержащий информацию о животных, цветах, деревьях и живописных местах. На диск было записано 7 часов звука, 100 анимационных роликов, примерно 800 масштабируемых карт, а также 7000 качественных фотографий. И все это — на одном диске! Напомним, что обычный компакт-диск в 650 Мбайт без использования компрессии может содержать либо 56 минут качественного звука, либо 1 час видео с разрешением 320 х 200 в формате MPEG-1, либо 700 полноцветных изображений размером 640 х 480.
В настоящее время алгоритмы, используемые для генерации изображений фрактальной графики, находят применение и в традиционных видах компьютерной графики: растровой и векторной. Например, в CorelDRAW эти алгоритмы используются для создания текстурных заливок. В недавно появившейся на рынке ПО растровой программе PhotoDraw 2000 фирмы Microsoft кроме стандартных градиентных заливок контуров можно сгенерировать фрактальный узор и воспользоваться им в качестве заливки.
Фрактал можно определить как объект довольно сложной формы, которая получена в результате выполнения простого итерационного цикла. Итерационность, рекурсивность процедуры создания обуславливают такие свойства фракталов, как самоподобие — отдельные части похожи по форме на весь фрактал в целом. Латинское fractus означает "составлен из фрагментов". В 1975 году французский математик Бенуа Мандельброт издал книгу "The fractal Geometry of Nature". Слово "фрактал" стало модным, и остается таковым и поныне.
Фракталом Мандельброта названа фигура, которая порождается очень простым циклом. Для создания этого фрактала необходимо для каждой точки изображения выполнить цикл итераций в соответствии с формулой:
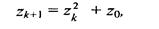
 где k = 0, 1,..., п. Величины zk — это комплексные числа, zk = хk + 1уk, причем стартовые значения х0 и у0 — это координаты точки изображения. Для каждой точки изображения итерации выполняются ограниченное количество раз (п) или до тех пор, пока модуль числа zk не превышает 2. Модуль комплексного числа равняется корню квадратному из х2 + у2. Для вычисления квадрата величины zk можно воспользоваться формулой z2 = (х + iy) (x + iy) = x2 - у2 + i2xy, поскольку i2 = -1. Цикл итераций для фрактала Мандельброта можно выполнять в диапазоне x = (от -2. 2, до 1), у = (от -1. 2 до 1. 2). Для того чтобы получить изображение в растре, необходимо пересчитывать координаты этого диапазона в пиксельные (рис. 5.1). Рис.5.1. Фрактал Мандельброта
где k = 0, 1,..., п. Величины zk — это комплексные числа, zk = хk + 1уk, причем стартовые значения х0 и у0 — это координаты точки изображения. Для каждой точки изображения итерации выполняются ограниченное количество раз (п) или до тех пор, пока модуль числа zk не превышает 2. Модуль комплексного числа равняется корню квадратному из х2 + у2. Для вычисления квадрата величины zk можно воспользоваться формулой z2 = (х + iy) (x + iy) = x2 - у2 + i2xy, поскольку i2 = -1. Цикл итераций для фрактала Мандельброта можно выполнять в диапазоне x = (от -2. 2, до 1), у = (от -1. 2 до 1. 2). Для того чтобы получить изображение в растре, необходимо пересчитывать координаты этого диапазона в пиксельные (рис. 5.1). Рис.5.1. Фрактал Мандельброта
Фрактал Жулиа совсем не похож на фрактал Мандельброта, однако, он определяется итерационным циклом, почти полностью тождественным циклу генерации Мандельброта. Формула итераций для фрактала Жулиа такова:
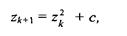
где с — комплексная константа.
Условием завершения итераций является | zk | > 2 — так же, как для фрактала Мандельброта.
Как видим, фрактал самоподобный — при любом увеличении отдельные части напоминают формы целого. Самоподобие считается важным свойством фракталов. Это отличает их от других типов объектов сложной формы.
Рассмотрим следующий пример фрактала — фрактал Ньютон. Для него итерационная формула имеет такой вид:
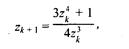
где z — также комплексные числа, причем z0 = x + iy соответствует координатам точки изображения.
Условием прекращения цикла итераций для фрактала Ньютон есть приближение значений |x4-1| к нулю.
Рассмотрим еще одну разновидность фракталов, названных геометрическими, поскольку их форма может быть описана как последовательность простых геометрических операций. Например, кривая Кох становится фракталом в результате бесконечного количества итераций, в ходе которых выполняется деление каждого отрезка прямой на три части. На рис. 5.2 показаны три итерации — постепенно линия становится похожей на снежинку.
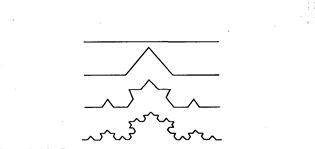
Рис. 5.2. Геометрические интерпретации для кривой Кох
Следующую группу составляют фракталы, которые генерируются согласно методу "систем итеративных функций" — IFS (Iterated Functions Systems). Этот метод может быть описан, как последовательный итеративный расчет координат новых точек в пространстве:
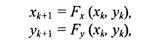
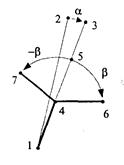 где Fx и Fy — функции преобразования координат, например, аффинного преобразования. Эти функции и обуславливают форму фрактала. В случае аффинного преобразования необходимо найти соответствующие числовые значения коэффициентов.
где Fx и Fy — функции преобразования координат, например, аффинного преобразования. Эти функции и обуславливают форму фрактала. В случае аффинного преобразования необходимо найти соответствующие числовые значения коэффициентов.
Рис. 5.3. Опорные точки элементов фрактала
Давайте попробуем разработать фрактал, который выглядел бы, как растение. Вообразим ствол, на котором много веточек. На каждой веточке много меньших веточек и так далее. Наименьшие ветви можно считать листвой или колючками. Все элементы будем рисовать отрезками прямой. Каждый отрезок будет определяться двумя конечными точками.
Для начала итераций необходимо задать стартовые координаты концов отрезка. Это будут точки 1, 2. На каждом шаге итераций будем рассчитывать координаты других точек.
Сначала находим точку 3. Это повернутая на угол α точка 2, центр поворота— в точке 1 (рис. 5.3):
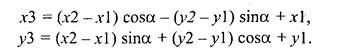
Если α = О, то ствол и все ветви прямые. Потом находим точку 4. От нее будут распространяться ветви. Пусть соотношение длин отрезков 1-4 и 1-3 равняется к, причем О < А: < 1. Тогда для вычисления координат точки 4 можно воспользоваться такими формулами:
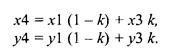
Теперь зададим длину и угол наклона ветвей, которые растут из точки 4. Сначала найдем координаты точки 5. Введем еще один параметр — к1, который будет определять соотношение длин отрезков 4-5 и 4-3, причем 0 < kl < 1. Координаты точки 5 равняются

Точки 6 и 7 — это точка 5, но повернутая относительно точки 4 на углы β и -β соответственно:
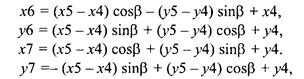
Кроме расчета опорных точек, на каждом шаге будем рисовать один отрезок 1 -4. В зависимости от номера итераций можно изменять цвет отрезка. Также можно устанавливать его толщину, например, пропорционально длине.
Таким образом, фрактал мы определили как последовательность аффинных преобразований координат точек. Величины а, β, к, k1 — это параметры, которые описывают вид фрактала в целом. Они являются константами на протяжении всего итеративного процесса. Это дает возможность в итерациях использовать только операции сложения, вычитания и умножения, если вычислить значения sin(), cos(), (1 - к) и (1 - k1) только один раз перед началом итераций как коэффициенты-константы.
Для того чтобы нарисовать фрактал, необходимо вызвать процедуру ШАГ, установив соответствующие значения ее аргументов: ШАГ(х1, у1, х2, у2, 0). Обратите внимание на один из аргументов этой процедуры — пит, который сначала имеет значение 0. В теле процедуры есть три рекурсивных вызова с разными значениями этого аргумента:
• ШАГ(х4, у4, х3, у3, num) —продолжаем СТВОЛ;
• ШАГ(х4, у4, х6, у6, num+l) —правая ветвь;
• ШАГ(х4, у4, х7, у7, num+1) —левая ветвь.
Значение пит показывает степень детализации расчета дерева. Один цикл итераций содержит много шагов, которые соответствуют одному значению величины пит. Числовое значение пит можно использовать для прекращения итеративного процесса, а также для определения текущего цвета элементов "растения".
Завершение циклов итераций в нашем алгоритме происходит тогда, когда длина ветви становится меньше некоторой величины lmin, например, lmin = 1.
Этот фрактал при α = 2°, β = 86°, к = 0. 14, k1 = 0. 3 похож на папоротник (рис. 5.4).
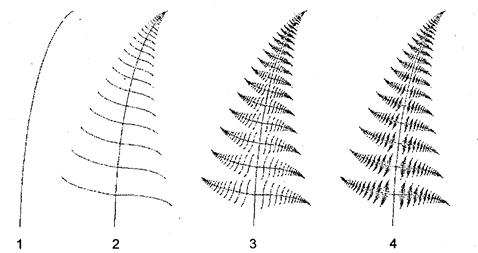
Рис. 5.4 Вид фрактала для разного количества циклов итераций
Метод IFS используется не только для создания изображений. Его использовали Барнсли и Слоан для эффективного сжатия графических изображений при записи в файл. Основная идея такая: поскольку фракталы могут представлять очень сложные изображения с помощью простых итераций, то описание этих итераций требует значительно меньшего объема информации, чем соответствующие растровые изображения. Для кодирования изображений необходимо решать обратную задачу — для изображения (или его фрагмента) подобрать соответствующие коэффициенты аффинного преобразования. Этот метод используется для записи цветных фотографий в файлы со сжатием в десятки и сотни раз без заметного ухудшения изображения. Формат таких графических файлов был назван FIF (Fractal Image Format) и запатентован фирмой Iterated Systems.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1331; Нарушение авторских прав?; Мы поможем в написании вашей работы!