Координаты векторов и точек

Пусть – произвольный базис пространства V ³. Существование хотя бы одного базиса гарантировано аксиомой D ₁.

По аксиоме D ₂ любые четыре вектора линейно зависимы. Пусть – произвольный вектор пространства V ³. Тогда существуют числа a, b, g, d, не равные нулю одновременно, что выполняется равенство .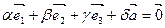

Если 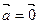, то в силу линейной независимости векторов 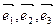(аксиома D ₁) получим, что a = b = g= 0, т.е. .

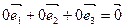Пусть 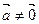, тогда 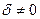. В противном случае a = b = g= 0. Вектор можно выразить через векторы 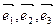: 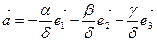. Обозначим 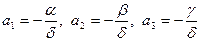, тогда

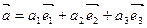. (3)

Доказали, что любой вектор 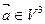можно разложить по векторам базиса, т.е. представить в виде (3).

Определение 19.

Координатами вектора относительно базиса называется упорядоченная тройка чисел 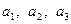, являющихся коэффициентами разложения (3) вектора по базису.

Обозначают: .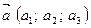

Таким образом, 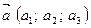Û .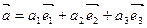

Докажем, что координаты вектора определяются однозначно. Допустим, что 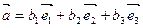. Тогда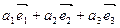 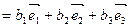, 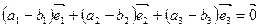. По аксиоме D ₁: , , 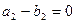, 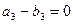т.е. .

Теорема 32

Координаты суммы векторов равны сумме соответствующих координат слагаемых векторов. Координаты произведения вектора на число равны произведению координат вектора на это же число.

Доказательство. Пусть – базис, l – произвольное действительное число, , 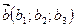. Тогда

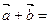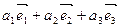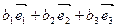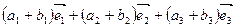()+()=, т.е.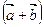 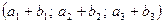по определению координат.

Пусть 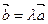, тогда 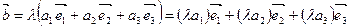, т.е. .

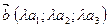Теорема доказана.

Следствие. Если 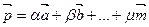, то

.

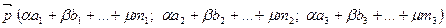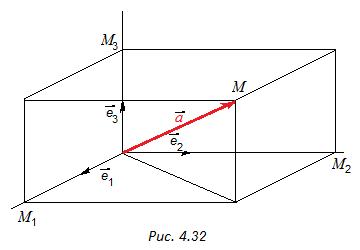Координаты линейной комбинации векторов равны точно таким же линейным комбинациям, составленным из соответствующих координат этих векторов.

Для того чтобы ввести координаты точек, к выбранному базису добавим точку О – начало координат. Получим аффинный репер 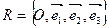(рис. 4.32).

Если дана точка М, то однозначно определяется вектор 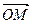, называемый вектором положения или радиус-вектором точки. Его координаты и будут координатами точки М.

Определение 20

Аффинными координатами точки М относительно репера 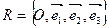называется упорядоченная тройка чисел 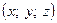, являющихся координатами радиус-вектора 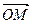относительно базиса .

Обозначение: .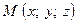

Таким образом, 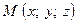Û .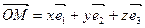

Любая тройка 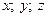действительных чисел определяет единственную точку пространства.

Действительно, если даны три числа 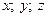, то однозначно определяется вектор 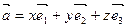. По аксиоме Т ₂ вектор можно однозначным образом отложить от точки О, т.е. и числа 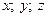являются по определению координатами точки .

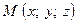Теорема 33

Если 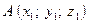, 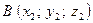в репере 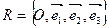, то 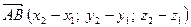в базисе .

Доказательство.

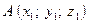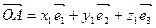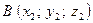Û . Û 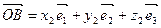. По аксиоме Т ₃ ,

=–=.

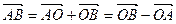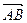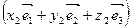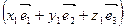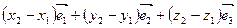По определению координат вектора .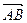

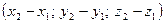Теорема доказана.

Дата добавления: 2014-01-05