Композиционных материалов

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ КОНСТРУИРОВАНИЯ

Требования, предъявляемые к армирующим волокнам и материалу матриц.

Волокна используются в качестве арматуры КМ. Они должны обладать небольшой плотностью, высокой прочностью во всем интервале рабочих температур, технологичностью, минимальной растворимостью в матрице, высокой химической стойкостью, отсутствием фазовых превращений в зоне рабочих температур и быть нетоксичными при изготовлении и эксплуатации. Для армирования применяют НК (усы), металлическую проволоку, неорганические и органические волокна. НК имеют диаметр от долей микрометра до нескольких микрометров и длину от долей миллиметра до нескольких сантиметров. Широко в качестве армирующих элементов конструкционных КМ они не используются.

Высокопрочная металлическая проволока из стали, вольфрама, молибдена и других металлов, хотя и имеет большую плотность и меньшую прочность, чем усы, благодаря своей технологичности, широкой доступности к сравнительно невысокой стоимости, используется в качестве арматуры, особенно для КМ на металлической основе, намного чаще, чем НК. Полукристаллические неорганические волокна, как и металлическая проволока, выпускаются промышленностью в больших количествах. Их недостатком является высокая чувствительность к механическим повреждениям, однако малая плотность, высокая прочность, химическая стойкость углеродных, борных, стеклянных, карбидокремниевых, кварцевых и других волокон позволяют широко использовать их для армирования пластмасс и металлов. Органические волокна используются для армирования полимерных матриц.

Роль матрицы в армированных КМ заключается в придании изделию необходимой формы и создании монолитного материала. Объединяя в одно целое многочисленные волокна, матрица позволяет композиции воспринимать различного рода внешние нагрузки: растяжение (как в направлении армирования, так и перпендикулярно ему), сжатие, изгиб, сдвиг и др. В то же время матрица должна принимать участие в создании несущей способности композиции, обеспечивая передачу усилий на волокна. За счет пластичной матрицы осуществляется также передача усилий от разрушенных или дискретных (коротких) волокон соседним волокнам и уменьшение концентрации напряжений вблизи различного рода дефектов. Матрица служит и защитным покрытием, предохраняющим волокна от механических повреждений и окисления.

Для разработки теории поведения армированных материалов при различных видах нагружения применяются макро- и микромеханический подходы. При макромеханическом подходе КМ рассматривается как однородная анизотропная среда, обладающая симметрией строения и свойств, которые зависят от свойств компонентов. Такой подход позволяет, использовав аппарат теории анизотропных сред для расчета макроскопических характеристик КМ, установить закономерности изменения свойств при изменении схемы напряженно-деформированного состояния. Однако замена реального неоднородного материала эквивалентным по прочности и жесткости гомогенным материалом не дает возможности определить поля напряжений и деформаций в микрообъемах КМ, в частности на межфазных границах.

Микромеханический подход предусматривает рассмотрение напряженно-деформированного состояния областей, соизмеримых с характерными размерам фаз КМ, и установление связи между механическими свойствами КМ и его компонентов. Задачей микромеханики является также анализ распределения напряжений и деформации внутри компонентов и на межфазных границах.

Закон Гука устанавливает связь между напряжениями σ, действующими на тело, и относительными упругими деформациями e, вызванными этими напряжениями. Для одноосного растяжения или сжатия изотропного тела закон Гука записывается в виде σ = Еe. Коэффициент пропорциональности Е называется модулем Юнга, или модулем нормальной упругости. Он служит константой изотропного материала, характеризующей его жесткость. Отношение относительной деформации образца в поперечном направлении e_y к его относительной упругой деформации в продольном направлении e_х называется коэффициентом Пуассона m: m = -e_y/e_х. Касательные напряжения t_ху и соответствующие упругие сдвиговые деформации g_ху связаны между собой: t_ху = Gg_ху. При гидростатическом сжатии изотропных тел закон Гука устанавливает прямую пропорциональность между гидростатическим давлением р и относительной упругой объемной деформацией D: р = kD. В общем случае связь между напряжениями и деформациями изотропного тела описывается обобщенным законом Гука, который в обозначениях, используемых в технике (технических обозначениях), имеет вид

; ;

; ;

; ;

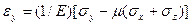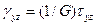Упругие постоянные Е, G, m и К связаны между собой соотношениями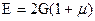, 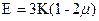. Только две из четырех констант независимы, а две другие могут быть вычислены из этих соотношений по двум известным.

При конструировании КМ проводят расчеты эксплуатационных характеристик. В подавляющем большинстве случаев требуется знать механические свойства будущего КМ – модули упругости, прочность и др.

Поясним физический смысл модулей упругости.

При нагружении образец подвергается вначале упругой а затем пластической деформации. Стадия упругой деформации имеет место при всех без исключения видах механических испытаний. Механизм упругой деформации состоит в обратимых смещениях атомов из положений равновесия в кристаллической решетке. Чем больше величина смещения каждого атома, тем больше упругая макродеформация всего образца. Величина этой упругой деформации в металлических и керамических материалах не может быть большой (относительное удлинение в упругой области обычно меньше 1%) так как атомы в кристаллической решетке способны упруго смещаться лишь на небольшую долю межатомного расстояния. Физический смысл модулей упругости как раз и состоит в том, что они характеризуют сопротивляемость материалов упругой деформации, т.е. смещению атомов из положений равновесия в решетке. Следовательно, модули упругости являются характеристиками сил связи в кристаллической решетке. Если сравнить два материала с разными Е, то для одинакового смещения атомов (равной упругой деформации) при большем Е потребуется большее напряжение. Единицы измерения модулей упругости: н/м²:

1 кг/мм² = 9,8·106 н/м² = 106 кг/м²

Дата добавления: 2014-01-05