Распределение напряжений по длине волокон

Выше уже говорилось о том, что от матрицы к волокну нагрузка передается касательными напряжениями τ, действующими на границе раздела. Эти напряжения, как и нормальные напряжения в волокнах, на концах волокна и в средней его части не одинаковы.

Разработано несколько моделей, позволяющих установить распределение напряжений. Приводят эти модели к качественно одинаковым результатам. Мы рассмотрим модель, предложенную Б. Розеном.

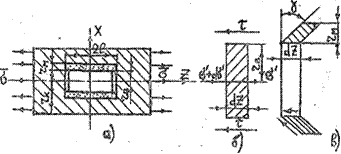
Рис. 2.12. К расчету распределения напряжений по длине волокна при растяжении однонаправленной композиции с дискретными волокнами: а – модель элемента КМ; б – элементарный отрезок волокна; в – элементарный отрезок матрицы в деформированном состоянии

Модель (рис. 2.12) представляет собой волокно радиусом r_в и длиной 2l, жестко связанное с тонким цилиндрическим слоем матричного материала толщиной r_м, который в свою очередь окружен оболочкой радиусом r_к из материала с осредненными свойствами КМ. Пусть ось волокна совпадает с осью z, а ось х проходит перпендикулярно к ней через середину волокна. Предполагается, что волокна несут только нормальные напряжения 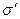, а матричный слой – только касательные напряжения τ, которые в этом слое локализуются, а в оболочке с осредненными свойствами композиции отсутствуют. Нагружена модель внешним 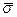, параллельным оси волокон, при этом торцы волокна в передаче напряжений участия не принимают.

Выделим элементарный отрезок волокна длиной dz (рис. 2.12, б) и запишем условие равновесия сил, действующих на него. Этот отрезок нагружен касательными напряжениями τ по периферии и нормальными 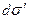по торцам. Суммарная сдвиговая нагрузка, действующая на него, равна 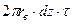, а суммарная нормальная . Условие равновесия запишется так:

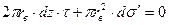
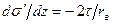(2.32)

Условие равновесия сил, действующих на всю модель в направлении оси z, при условии, что матрица не несет нормальных нагрузок, можно записать в виде:

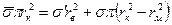
где:

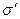– нормальное напряжение в осредненном КМ.

Под действием касательных напряжений τ матричный слой и вместе с ним осредненный КМ сдвигаются по отношению к волокну. Для элементарного отрезка матрицы (рис. 2.12, в) тангенс угла сдвига равен:

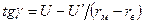
где:

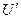– осевое перемещение волокна;

U – осевое перемещение осредненного КМ.

Предположим, что волокно, матрица и осредненный КМ деформируются упруго и, следовательно, подчиняются закону Гука. В силу малости угла g можно считать, что tgg» g, и записать

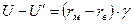
Продифференцируем обе части этого равенства по z, учитывая при этом известные из сопротивления материалов соотношения 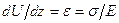и 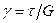, где e – относительная деформация, Е и G – модули нормальной упругости и сдвига. Тогда получим:

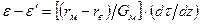
или

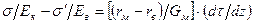
здесь e и 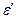– относительные линейные деформации осредненного КМ и волокна соответственно; Е_к и Е _в – модули Юнга осредненного КМ и волокна соответственно; G – модуль сдвига матрицы.

После преобразований получим дифференциальное уравнение относительно касательных напряжений τ:

,

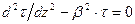где:

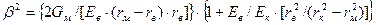
Решение уравнения для τ имеет вид:

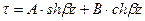
где знаки sh и сh обозначают гиперболический синус и косинус, соответственно:

;

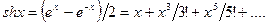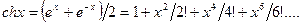
Используя граничные условия τ = 0 при z = 0 и 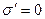при z = 1 (начало координат находится в середине волокна), приходим к уравнениям, устанавливающим зависимость касательных и нормальных напряжений от координаты z:

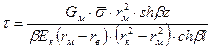
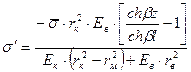
Нормальные напряжения 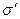в волокне увеличиваются от концов волокон к его середине, достигая при z = 0 максимального значения:

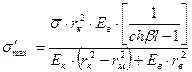
Касательные напряжения имеют наибольшее значение на конце волокна (при z = l) и уменьшаются до нуля в его середине (при z = 0). Распределение нормальных и касательных напряжений по длине волокна представлено на рис. 2.13.

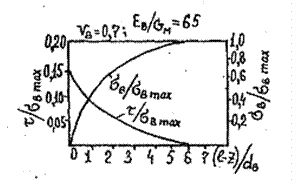
Рис. 2. 13. Распределение нормальных и касательных напряжений по длине волокна при растяжении КМ, содержащего 70% (объемн.) волокон

(отношение модулей упругости волокна и матрицы Е_м/G_м = 65)

Если принять, что r_к >> r_м, то безразмерный параметр β» 2G/[r_вЕ_в(r_м – r_в)]. И тогда

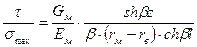
(2.33)

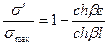
где:

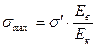– максимальное нормальное напряжение в бесконечно длинном волокне.

Если матрица проявляет пластические свойства, то концентрация касательных напряжений у концов волокна уменьшается, однако характер измерения напряжений по длине остается тем же.

Дата добавления: 2014-01-05