Магнитное поле прямого тока

Линии вектора магнитной индукции прямолинейного проводника с током представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику (рис. 69.1), центры которых совпадают с положением проводника. Направление линий вектора 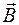связано с направлением тока в проводнике правилом правого винта.

Используя закон Био–Савара, рассчитаем индукцию магнитного поля прямолинейного проводника с током в точке А, расположенной на расстоянии R от проводника (рис. 69.2). В точке А все элементарные векторы 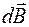направлены в одну сторону, поэтому геометрическую сумму векторов 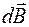можно заменить их арифметической суммой. Но тогда в соответствии с формулой (68.3)

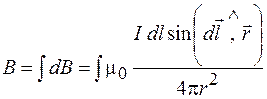. (69.1)

Из рисунка 69.2 следует: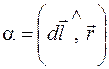; АС = AD = r; СЕ AD, величины 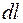и 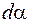малы. Из CDE находим:

. (69.2)

Из АСЕ получаем:

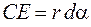. (69.3)

Из соотношений (69.2) и (69.3) следует:

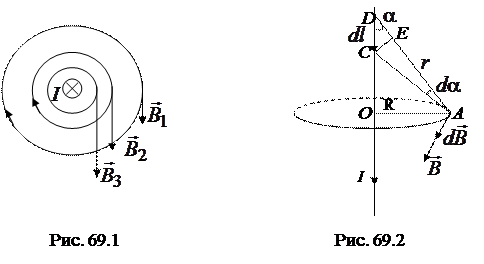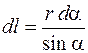. (69.4)

Так как из ADO видно, что

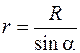, (69.5)

то, объединяя формулы (69.1), (69.4), (69.5), получаем:

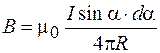. (69.6)

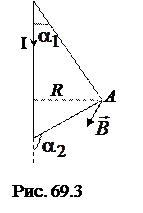
Если проводник имеет конечные размеры (рис. 69.3), то угол меняется в пределах от 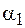до 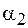. Тогда из выражения (69.6) находим:

.

Вычисляя этот интеграл, имеем:

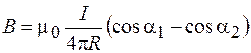. (69.7)

Если проводник бесконечно длинный, то для него , 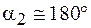. Тогда из формулы (69.7) получаем:

. (69.8)

Из выражения (69.8) следует, что индукция магнитного поля линейного длинного проводника пропорциональна силе тока I в нем и обратно пропорциональна расстоянию R до него.

Если магнитное поле, в котором находится длинный проводник 1 с током , создано другим током 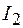, текущим по прямолинейному длинному проводнику 2 (рис. 69.4), то на элемент длины 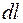проводника 1 будет действовать сила Ампера, равная по модулю

,

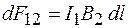где .

После подстановки получим:

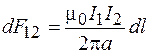. (69.9)

Отсюда сила, действующая на единицу длины проводника 1, равна

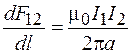. (69.10)

Аналогично определяется сила, действующая на единицу длины проводника 2. Эти силы равны. Направление сил определяется по правилу левой руки.

Таким образом, два параллельных тока одинакового направления притягиваются, а противоположного – отталкиваются.

Магнитное взаимодействие двух параллельных токов используется в определении единицы силы тока в единицах СИ. Один ампер – сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 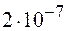Н.

Дата добавления: 2014-01-05