Магнитное поле соленоида

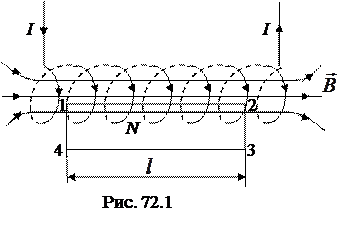Соленоидом называют длинную катушку, состоящую из большого числа круговых токов, плотно навитых на цилиндрический каркас (рис. 72.1). Если длина соленоида значительно больше его диаметра, то его называют бесконечно длинным. В этом случае магнитное поле сосредоточено полностью внутри соленоида и является однородным. Направление вектора 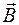определяется по правилу правого винта, как для кругового тока. Для расчета магнитного поля бесконечно длинного соленоида воспользуемся законом полного тока (71.3). Для этого выберем прямоугольный контур 1–2–3–4–1 с длиною l стороны 1–2, охватывающий N витков с током. Тогда циркуляцию вектора 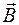можно представить как сумму линейных интегралов по отдельным участкам контура, т. е.

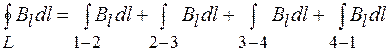, (72.1)

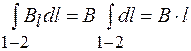, (72.2)

так как во всех точках внутри соленоида вектор 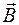одинаков и направлен вдоль участка 1–2 контура:

, (72.3)

так как для участков, лежащих внутри соленоида 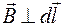, а за пределами соленоида поле отсутствует, т. е. .

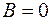Объединяя формулы (72.1)–(72.3), получаем:

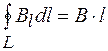. (72.4)

Так как по отношению к контуру L все N токов направлены одинаково, то

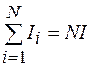. (72.5)

Подставив в формулу (71.3) соотношения (72.4) и (72.5), получим , откуда

. (72.6)

Обозначив число витков, приходящихся на единицу длины соленоида , через 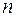, получим:

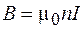. (72.7)

Если соленоид содержит сердечник из вещества с магнитной проницаемостью 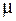, то

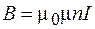. (72.8)

Дата добавления: 2014-01-05