Уравнения плоской и сферической волн. Волновой вектор

Для характеристики формы волны вводится понятие волновой поверхности. Волновой поверхностью называется поверхность, в каждой точке которой фаза колебаний имеет постоянное значение. Если волновая поверхность представляет собой плоскость, то такая волна называется плоской волной. Сферической волной называется волна, волновая поверхность которой имеет форму сферы.

Направление распространения волны характеризуют волновым вектором. Волновым вектором называется вектор, направленный по нормали к волновой поверхности в сторону распространения волны, модуль которого равен волновому числу . Для плоской волны волновой вектор имеет постоянное значение в каждой точке волновой

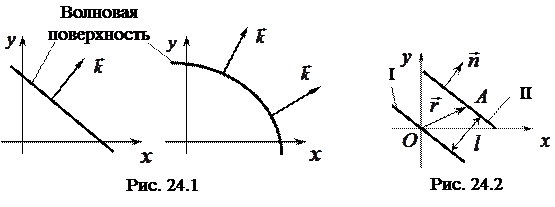поверхности (по модулю и направлению). Для волн более сложной формы направление волнового вектора в разных точках волновой поверхности будет различным (рис. 24.1).

Рассмотрим плоскую монохроматическую волну, распространяющуюся в произвольном направлении. Выберем начало координат таким образом, чтобы волновая поверхность в момент времени 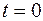проходила через начало координат (положение I на рис. 24.2). Пусть в каждой точке этой волновой поверхности колебания описываются уравнением 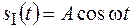. Через некоторое время 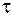волна пройдет расстояние 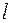и волновая поверхность I переместится в положение II, причем , где – скорость распространения волны. Тогда в каждой точке волновой поверхности II колебания будут описываться уравнением 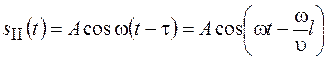. Для произвольной точки А волновой поверхности II с радиусом-вектором 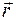можно записать 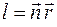, где 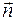– единичный вектор нормали к волновой поверхности, направленный в сторону распространения волны. С учетом этого уравнения колебания в точке А будут иметь вид

. (24.1)

Так как 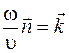, то выражение (24.1) можно записать в виде

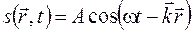. (24.2)

Уравнение (24.2) есть уравнение плоской волны, распространяющейся в произвольном направлении, определяемом волновым вектором . В комплексной форме это же уравнение можно представить в виде

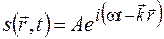. (24.3)

Выразив скалярное произведение векторов через их проекции, уравнение (24.2) можно преобразовать следующим образом:

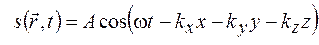, (24.4)

где 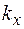, , 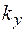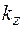– проекции волнового вектора на соответствующие координатные оси.

Если координатные оси выбрать таким образом, чтобы положительное направление оси 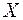совпало с направлением распространения волны, то волновой вектор будет иметь проекции 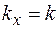, 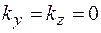и уравнение плоской волны примет вид

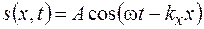. (24.5)

Сферические волны излучаются точечным источником. Если в начале координат находится точечный источник, который создает гармонические колебания 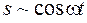, то в точку 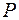, удаленную на расстояние 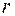от источника, эти колебания будут приходить с запаздыванием 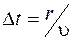, где – скорость распространения волн. Тогда колебания в точке 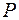будут иметь вид

,

где 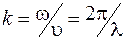– волновое число. Интенсивность волны пропорциональна квадрату ее амплитуды. При отсутствии потерь энергия, переносимая волной в единицу времени через сферическую волновую поверхность, должна быть постоянной. Так как площадь сферы пропорциональна квадрату радиуса, то для постоянства энергии амплитуда сферической волны должна убывать обратно пропорционально расстоянию. Таким образом, уравнение сферической волны имеет вид

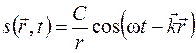. (24.6)

В комплексной форме уравнение сферической волны имеет вид

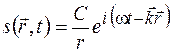. (24.7)

Реальные источники волн имеют конечные размеры, поэтому сферические волны получаются на достаточно большом удалении от источника, когда его размерами можно пренебречь по сравнению с расстоянием до него.

Дата добавления: 2014-01-05