
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вектор Умова
|
|
|
|
Энергетические характеристики упругих волн.
Пусть в среде распространяется плоская монохроматическая волна (24.5). Выберем малый объем 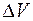 такой, чтобы скорость всех частиц и относительную деформацию
такой, чтобы скорость всех частиц и относительную деформацию 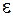 можно было считать постоянными по всему объему. Скорость частиц найдем, дифференцируя смещение
можно было считать постоянными по всему объему. Скорость частиц найдем, дифференцируя смещение 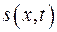 по времени
по времени 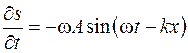 .
.
Кинетическая энергия объема 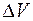
 .
.
Объем 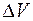 вследствие упругой деформации будет обладать также потенциальной энергией, причем для бегущей волны в каждый момент времени кинетическая и потенциальная энергии равны и изменяются в одинаковой фазе. Это является существенным отличием волнового процесса от колебаний в системе с сосредоточенными параметрами, где изменения кинетической и потенциальной энергий происходят в противофазе (см. § 4). С учетом этого для полной механической энергии объема можно записать
вследствие упругой деформации будет обладать также потенциальной энергией, причем для бегущей волны в каждый момент времени кинетическая и потенциальная энергии равны и изменяются в одинаковой фазе. Это является существенным отличием волнового процесса от колебаний в системе с сосредоточенными параметрами, где изменения кинетической и потенциальной энергий происходят в противофазе (см. § 4). С учетом этого для полной механической энергии объема можно записать
 .
.
Тогда объемная плотность энергии упругой волны
 . (27.1)
. (27.1)
Из (27.1) видно, что объемная плотность энергии изменяется с удвоенной частотой  и пропорциональна квадрату частоты и амплитуды волны. Усредняя (27.1) за период колебаний
и пропорциональна квадрату частоты и амплитуды волны. Усредняя (27.1) за период колебаний 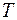 , найдем среднее значение объемной плотности энергии:
, найдем среднее значение объемной плотности энергии:
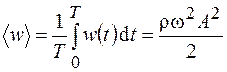 . (27.2)
. (27.2)
Возьмем произвольную поверхность 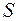 . Количество энергии, переносимой волной через эту поверхность в единицу времени, называется потоком энергии
. Количество энергии, переносимой волной через эту поверхность в единицу времени, называется потоком энергии  :
:
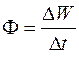 . (27.3)
. (27.3)
Как следует из определения, поток энергии измеряется в ваттах (Вт).
Если поверхность 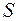 перпендикулярна направлению распространения волны, а ее площадь
перпендикулярна направлению распространения волны, а ее площадь  мала, то за малое время
мала, то за малое время 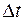 через эту поверхность будет перенесена энергия
через эту поверхность будет перенесена энергия  , заключенная в объеме
, заключенная в объеме 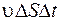 , где
, где  – скорость волны. Так как объем мал, то, полагая, что объемная плотность энергии в этом объеме постоянная, получим
– скорость волны. Так как объем мал, то, полагая, что объемная плотность энергии в этом объеме постоянная, получим 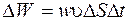 . Разделив обе части последнего равенства на
. Разделив обе части последнего равенства на 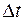 , найдем поток энергии
, найдем поток энергии 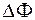 через поверхность
через поверхность 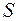 :
:
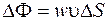 . (27.4)
. (27.4)
Отношение потока энергии, переносимого волной через поверхность 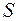 , перпендикулярную направлению распространения волны, к площади этой поверхности называют плотностью потока энергии
, перпендикулярную направлению распространения волны, к площади этой поверхности называют плотностью потока энергии 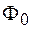 , т. е.
, т. е.  . Плотность потока измеряется в
. Плотность потока измеряется в 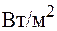 . Введем вектор Умова
. Введем вектор Умова 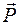 ;
;
 . (27.5)
. (27.5)
Вектором Умова называется вектор, направленный в сторону распространения волны (т. е. перпендикулярно волновой поверхности), величина которого равна произведению объемной плотности энергии и скорости распространения волны. Из (27.4) следует, что вектор Умова численно равен количеству энергии, переносимой волной в единицу времени через единицу площади поверхности, перпендикулярной направлению распространения волны. Единица измерения вектора Умова – 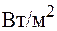 . Зная вектор Умова
. Зная вектор Умова 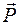 , можно найти поток энергии через произвольную поверхность
, можно найти поток энергии через произвольную поверхность 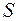 по формуле
по формуле
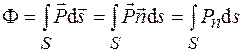 , (27.6)
, (27.6)
где 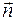 – единичный вектор нормали к поверхности
– единичный вектор нормали к поверхности 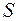 ;
; 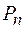 – проекция вектора Умова на нормаль
– проекция вектора Умова на нормаль 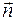 к поверхности
к поверхности 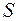 .
.
Интенсивностью волны 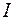 называется среднее за период
называется среднее за период 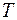 значение потока энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны. Интенсивность волны равна среднему значению модуля вектора Умова и так же, как и вектор Умова, измеряется в
значение потока энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны. Интенсивность волны равна среднему значению модуля вектора Умова и так же, как и вектор Умова, измеряется в 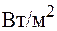 , т. е.
, т. е.
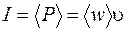 . (27.7)
. (27.7)
Подставляя вместо  выражение (27.2), получим
выражение (27.2), получим
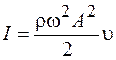 . (27.8)
. (27.8)
Из этого выражения следует, что интенсивность волны пропорциональна квадрату частоты и амплитуды.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 9323; Нарушение авторских прав?; Мы поможем в написании вашей работы!