С временными рядами

Использование фиктивных переменных в моделях

В регрессионных моделях с временными рядами используется три основных вида фиктивных переменных:

1) Переменные-индикаторы принадлежности наблюдения к определенному периоду — для моделирования скачкообразных структурных сдвигов. Границы периода (моменты “скачков”) должны быть установлены из априорных соображений.

Например, 1, если наблюдение принадлежит периоду 1941-45 гг. и 0 в противном случае. Это пример использования для моделирования временного структурного сдвига.

Постоянный структурный сдвиг моделируется переменной равной 0 до определенного момента времени и 1 для всех наблюдений после этого момента времени.

2) Сезонные переменные — для моделирования сезонности.

Сезонные переменные принимают разные значения в зависимости от того, какому месяцу или кварталу года или какому дню недели соответствует наблюдение.

Например,модель потребления, учитывающая сезонные колебания.

у = b₀ + b1x1 + b₂x₂ + b₃x₃,

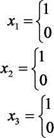
для зимних месяцев

иначе

для весенних месяцев

иначе

для летних месяцев

иначе

Следует отметить, что вводить четвертую переменную х₄ для осенних месяцев не требуется, т.к. в этом случае все переменные оказались бы связанными тождеством

Xi +Х₂+Хз+Х₄= 1,

что привело бы их к полной коллинеарности и вырожденности информационной матрицы .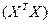

Для осенних месяцев коэффициенты b1, b₂, b3 равны нулю и объем потребления составляет Y= b0

Для зимних месяцев: Y=b0 + b1,

Для весенних месяцев: Y=b0 + b₂,

Для летних месяцев: Y=b0 + b3.

При этом, если в результате регрессионного анализа окажется, что b3 = 0, это означает, что между летними и осенними сезонами различие в потреблении несущественно. При b1 = b₂ отсутствует различие между потреблением зимой и весной и т.д.

3) Линейный временной тренд — для моделирования постепенных плавных структурных сдвигов.

Эта фиктивная переменная показывает, какой промежуток времени прошел от некоторого “нулевого” момента времени до того момента, к которому относится данное наблюдение (координаты данного наблюдения на временной шкале).

Если промежутки времени между последовательными наблюдениями одинаковы, то временной тренд можно составить из номеров наблюдений.

Временной тренд отличается от бинарных фиктивных переменных тем, что имеет смысл использовать его степени: t ² , t ³ и т. д. Они помогают моделировать гладкий, но нелинейный тренд. (Бинарную переменную нет смысла возводить в степень, потому что в результате получится та же самая переменная.)

Можно также комбинировать указанные виды фиктивных переменных, создавая переменные “взаимодействия” соответствующих эффектов.

Комбинация рассмотренных фиктивных переменных позволяет моделировать еще один эффект — изменение наклона тренда с определенного момента.

Помимо тренда в регрессию следует тогда ввести следующую переменную: в начале выборки до некоторого момента времени она равна 0, а вторая ее часть представляет собой временной тренд (1, 2, 3 и т. д. в случае одинаковых интервалов между наблюдениями).

Использование фиктивных переменных имеет следующие преимущества:

1) Интервалы между наблюдениями не обязательно должны быть одинаковыми. В выборке могут быть пропущенные наблюдения.

2) Коэффициенты при фиктивных переменных легко интерпретировать, они наглядно представляют структуру динамического процесса.

3) Для оценивания модели не приходится выходить за рамки классического метода наименьших квадратов.

Дата добавления: 2014-01-05