Предел функции

Определение. Будем говорить, что последовательность точек сходится при к точке , если при .

В этом случае точку называют пределом указанной последовательности и пишут: 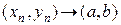при .

Легко показать, что 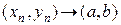тогда и только тогда, когда одновременно 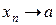, 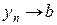(т.е. сходимость последовательности точек пространства 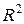эквивалентна покоординатной сходимости).

Пусть 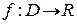и 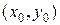– предельная точка множества .

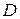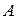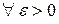
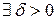Определение. Число называют пределом функции при , если для такое, что 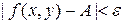, как только . В этом случае пишут

или при .

При кажущейся полной аналогии понятий предела функций одной и двух переменных существует глубокое различие между ними. В случае функции одной переменной для существования предела в точке необходимо и достаточно равенство лишь двух чисел – пределов по двум направлениям: справа и слева от предельной точки 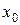. Для функции двух переменных стремление к предельной точке 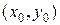на плоскости 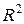может происходить по бесконечному числу направлений (и необязательно по прямой), и потому требование существования предела у функции двух (или нескольких) переменных «жестче» по сравнению с функцией одной переменной.

Пример. Найти .

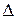Пусть стремление к предельной точке 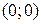происходит по прямой 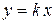. Тогда

.

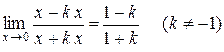Предел, очевидно, не существует, так как число 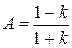зависит от . ▲

Пример. Найти .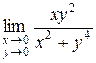

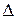По любой прямой 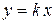предел один и тот же:

.

С другой стороны, пусть стремление к предельной точке происходит по кривой . Тогда

;

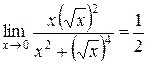следовательно, предел не существует. ▲

Сформулируем понятие предела функции для случая, когда предельная точка имеет бесконечные координаты. Ограничимся случаем, когда , (остальное – по аналогии).

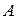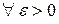
Определение. Число называют пределом функции при и , если для такое, что из неравенств 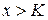и следует неравенство 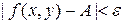. Этот факт коротко записывают так:

.

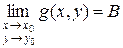Теорема 1. Если существуют и , то:

;

;

,

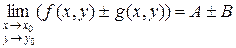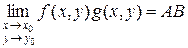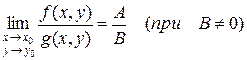где предельная точка 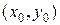может быть конечной или бесконечной.

Справедливы аналоги и других теорем о свойствах пределов функций одной переменной.

3. Непрерывность функции. Пусть дана функция с областью определения 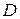и пусть 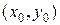– предельная точка множества .

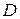Определение. Говорят, что функция непрерывна в точке 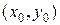, если:

1) ;

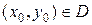2) 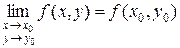, т.е. .

Сформулируем определение непрерывности в эквивалентной форме. С этой целью обозначим , и .

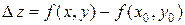Определение. Говорят, что функция непрерывна в точке 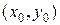, если выполняется равенство

.

Теорема 2. Если функци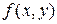и и непрерывны в точке 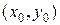, то этим же свойством обладают функци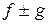и , , а если , то и функция .

Если мы хотим ввести понятие непрерывной функции на множестве, как функции, непрерывной в каждой точке множества, то само определение непрерывности в точке требует, чтобы каждая точка множества принадлежала ему (либо с некоторой своей 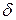-окрестностью, либо как его граничная точка).

Определение. Множество 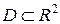называется областью, если оно:

1) является открытым множеством, т.е. содержит каждую свою точку вместе с некоторой своей 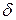-окрестностью; 2) является линейно связным множеством, т.е. для любых двух различных точек 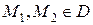существует ломаная, соединяющая 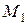и 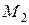и целиком лежащая в .

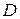Если 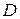– область, то множество называют замкнутой областью.

Определение. Говорят, что функция 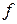непрерывна в области 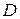(или в замкнутой области ), если 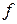непрерывна в каждой точке этого множества.

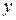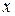4. Непрерывность по отдельным переменным. Зафиксируем переменную , полагая , а переменной придадим произвольное приращение 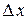. Функция получит приращение

,

которое называется частным приращением функции в точке 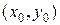, соответствующим приращению 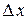аргумента 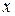. Заметим, что 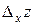является функцией одной переменной 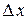. Аналогично,

.

Определение. Функция называется непрерывной в точке 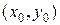по переменной 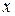(по переменной 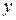), если

().

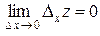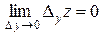В отличие от непрерывности по отдельным переменным обычную непрерывность функции называют иногда непрерывностью по совокупности переменных.

Теорема 3. Если функция определена в некоторой окрестности точки 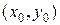и непрерывна в этой точке, то она непрерывна в этой точке по каждой из переменных.

Обратное утверждение неверно.

Пример. Докажем, что функция

непрерывна в точке 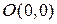по каждой переменно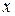й и 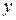, но не является непрерывной в этой точке по совокупности переменных.

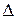Рассмотрим частное приращение функции 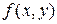в точке 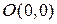, соответствующее приращению 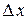аргумента :

.

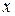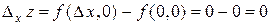Очевидно, что 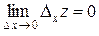, а это означает, что 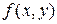непрерывна в точке 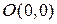по переменной .

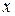Аналогично можно доказать непрерывность 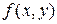в точке 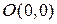по переменной .

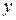Покажем, что предел 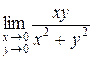не существует. Пусть точка 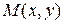стремиться к точке 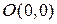по прямой 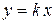, проходящей через точку 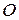. Тогда получим

.

Таким образом, приближаясь к точке 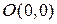по различным прямым, соответствующим разным значениям , получаем разные предельные значения. Отсюда следует, что предел данной функции в точке 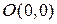не существует, а значит, функция 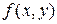не является непрерывной в этой точке. ▲

Дата добавления: 2014-01-05