
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частные производные и дифференцируемость функции
|
|
|
|
1. Частные производные первого порядка. Пусть функция  определена в области
определена в области 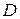 и
и 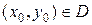 . Тогда при малых
. Тогда при малых 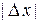 определено ее частное приращение по
определено ее частное приращение по 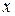 :
:  .
.
Определение. Частной производной функции 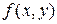 по переменной
по переменной 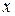 в точке
в точке 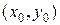 называют предел
называют предел
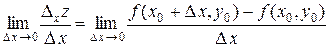 ,
,
если он существует.
Частную производную по 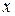 обозначают одним из следующих символов:
обозначают одним из следующих символов:
 .
.
Аналогично определяется частная производная по 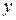 и вводятся ее обозначения.
и вводятся ее обозначения.
Легко видеть, что частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной.
Пример. Найти частные производные функции 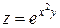 .
.
 Имеем:
Имеем:
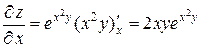 ,
, 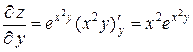 . ▲
. ▲
2. Частные производные высших порядков. Рассматривая частные производные  и
и 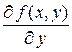 как функции от
как функции от  , приходим к понятиям частных производных второго порядка. А именно, выражения
, приходим к понятиям частных производных второго порядка. А именно, выражения
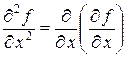 ,
, 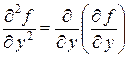
называют частными производными второго порядка функции 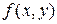 по
по 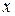 и по
и по 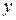 соответственно, а выражения
соответственно, а выражения
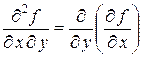 ,
, 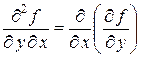
– смешанными частными производными второго порядка функции 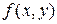 . Их обозначают также символами:
. Их обозначают также символами: 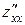 ,
, 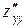 ,
, 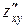 и
и 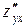 . Аналогично определяют частные производные 3-го порядка (их будет 8=23 ), 4-го порядка (их будет 16=24 ) и т.д.
. Аналогично определяют частные производные 3-го порядка (их будет 8=23 ), 4-го порядка (их будет 16=24 ) и т.д.
Теорема 4. Если в некоторой окрестности точки 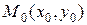 функция
функция  имеет смешанные частные производные
имеет смешанные частные производные 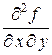 и
и 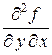 , причем эти производные непрерывны в точке
, причем эти производные непрерывны в точке 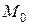 , то они равны в этой точке:
, то они равны в этой точке:
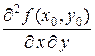 =
= .
.
Если последнее равенство выполняется, то говорят, что смешанные частные производные 2-го порядка функции  не зависят от порядка дифференцирования в точке
не зависят от порядка дифференцирования в точке 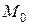 .
.
Теорема 4 допускает обобщение: по индукции ее можно распространить на любые непрерывные смешанные частные производные.
3. Дифференцируемость функции. Пусть 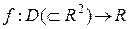 . Составим полное приращение функции
. Составим полное приращение функции  в точке
в точке 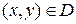 :
:
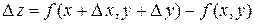 .
.
Определение. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 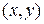 , если ее полное приращение в этой точке можно представить в виде
, если ее полное приращение в этой точке можно представить в виде
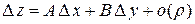 , (1)
, (1)
где 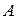 и
и 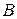 – некоторые числа,
– некоторые числа, 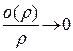 при
при 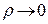 ,
, 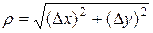 .
.
Другими словами, функция  дифференцируема в точке
дифференцируема в точке 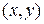 , если ее приращение
, если ее приращение 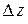 эквивалентно функции
эквивалентно функции 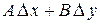 :
:  при
при 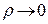 . Выражение
. Выражение 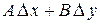 в этом случае представляет собой главную часть приращения
в этом случае представляет собой главную часть приращения 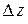 , линейно зависящую от
, линейно зависящую от 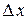 и
и 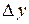 .
.
Определение. Если функция  дифференцируема в точке
дифференцируема в точке 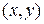 , то главную линейную часть
, то главную линейную часть 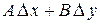 ее приращения
ее приращения 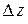 называют полным дифференциалом в точке
называют полным дифференциалом в точке 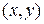 и обозначают в виде
и обозначают в виде
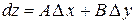 .
.
Для независимых переменных 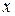 и
и 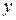 полагают
полагают 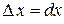 и
и 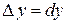 . Поэтому полный дифференциал записывают также в виде
. Поэтому полный дифференциал записывают также в виде
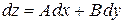 .
.
Формула (1) показывает, что, как и в случае функции одной переменной, верна
Теорема 5. Если функция 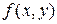 дифференцируема в точке
дифференцируема в точке 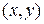 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Обратное утверждение неверно, т.е. непрерывность является только необходимым, но не достаточным условием дифференцируемости функции. Покажем это.
Пример.  Найдем частные производные функции
Найдем частные производные функции 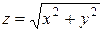 :
:
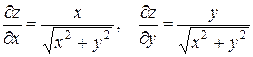 .
.
Полученные формулы теряют смысл в точке 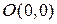 .
.
Можно показать иначе, что функция 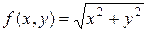 не имеет частных производных в точке
не имеет частных производных в точке 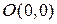 . В самом деле,
. В самом деле, 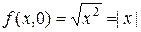 . Эта функция одной переменной
. Эта функция одной переменной 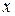 , как известно, не имеет производной в точке
, как известно, не имеет производной в точке 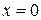 . Последнее и означает, что частная производная
. Последнее и означает, что частная производная 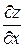 в точке
в точке 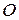 не существует. Аналогично, не существует частная производная
не существует. Аналогично, не существует частная производная 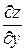 . При этом функция
. При этом функция 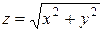 , очевидно, непрерывна в точке
, очевидно, непрерывна в точке  . ▲
. ▲
Итак, мы показали, что непрерывная функция может не иметь частных производных. Осталось установить связь между дифференцируемостью и существованием частных производных.
4. Связь между дифференцируемостью и существованием частных производных. Напомним, что для функции одной переменной 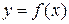 существование производной в точке является необходимым и достаточным условием дифференцируемости функции в этой точке. Для функции многих переменных дифференцируемость и существование частных производных не являются эквивалентными свойствами функции.
существование производной в точке является необходимым и достаточным условием дифференцируемости функции в этой точке. Для функции многих переменных дифференцируемость и существование частных производных не являются эквивалентными свойствами функции.
Теорема 6 (необходимое условие дифференцируемости). Если функция  дифференцируема в точке
дифференцируема в точке 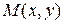 , то она имеет в точке
, то она имеет в точке 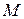 частные производные по каждой переменной
частные производные по каждой переменной 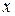 и
и 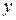 .
.
При этом 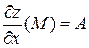 ,
,  , где
, где 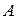 и
и 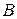 – числа из равенства (1). Поэтому условие дифференцируемости (1) можно записать в виде
– числа из равенства (1). Поэтому условие дифференцируемости (1) можно записать в виде
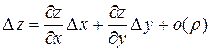 ,
,
а полный дифференциал функции – в виде
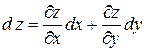 .
.
Обратная теорема не верна, т.е. существование частных производных не является достаточным условием дифференцируемости функции.
Теорема 7 (достаточное условие дифференцируемости). Если функция  имеет непрерывные частные производные
имеет непрерывные частные производные 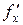 и
и 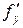 в точке
в точке 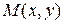 , то она дифференцируема в точке
, то она дифференцируема в точке 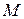 (и ее полный дифференциал в этой точке выражается формулой
(и ее полный дифференциал в этой точке выражается формулой 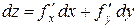 ).
).
Обратная теорема не верна, т.е. непрерывность частных производных является только достаточным, но не необходимым условием дифференцируемости функции.
5. Геометрический смысл дифференцируемости функции. Напомним, что для функции одной переменной 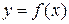 из дифференцируемости функции в точке
из дифференцируемости функции в точке 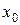 следует существование касательной к графику функции в точке
следует существование касательной к графику функции в точке 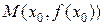 .
.
Рассмотрим непрерывную функцию двух переменных  ,
,  . График этой функции, т.е. множество точек
. График этой функции, т.е. множество точек  , представляет собой поверхность в пространстве
, представляет собой поверхность в пространстве 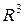 . Пусть плоскость
. Пусть плоскость  проходит через точку
проходит через точку 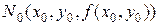 поверхности
поверхности 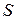 ;
; 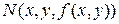 – произвольная (текущая) точка поверхности
– произвольная (текущая) точка поверхности 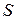 ;
; 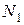 – ос
– ос
 |
нование перпендикуляра, проведенного из точки
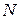 к плоскости
к плоскости  (рис. 6).
(рис. 6).
Рис. 6.
Определение. Плоскость  , проходящая через точку
, проходящая через точку 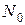 поверхности
поверхности 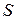 , называется касательной плоскостью к поверхности
, называется касательной плоскостью к поверхности 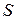 в этой точке, если при
в этой точке, если при 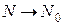 (
(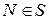 ) величина
) величина 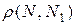 является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем 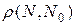 , т.е.
, т.е.  .
.
Теорема 8. Если функция  дифференцируема в точке
дифференцируема в точке 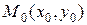 , то в точке
, то в точке 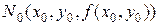 существует касательная плоскость к поверхности
существует касательная плоскость к поверхности 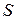 (графику этой функции), причем уравнение касательной плоскости имеет вид
(графику этой функции), причем уравнение касательной плоскости имеет вид
 .
.
Вектор 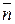 нормали к касательной плоскости, т.е.
нормали к касательной плоскости, т.е. 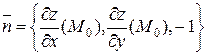 , называется вектором нормали (или нормалью) к поверхности
, называется вектором нормали (или нормалью) к поверхности 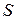 в точке
в точке 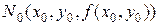 .
.
Пример. Составить уравнение касательной плоскости к параболоиду 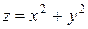 в точке
в точке 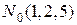 и найти нормаль к параболоиду в этой точке.
и найти нормаль к параболоиду в этой точке.
 Пусть
Пусть 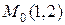 – точка на плоскости
– точка на плоскости 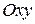 . Так как
. Так как 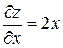 ,
, 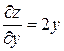 , то
, то  ,
, 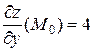 . Учитывая также, что
. Учитывая также, что 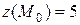 , получаем искомое уравнение касательной плоскости:
, получаем искомое уравнение касательной плоскости:
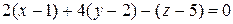 , или
, или 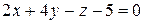 .
.
Вектор 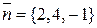 является нормалью к параболоиду в точке
является нормалью к параболоиду в точке 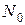 . ▲
. ▲
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 519; Нарушение авторских прав?; Мы поможем в написании вашей работы!