Предел функции многих переменных. Непрерывность

П. 1. Основные определения. Функция многих переменных. Множества.

Предел, непрерывность. Частные производные, дифференцируемость.

Функции многих переменных. Основные определения.

Лекция 1

Рассмотрим евклидовы пространства , 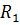. Пусть 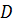- некоторое множество в евклидовом пространстве 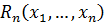(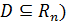, 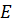- некоторое множество в пространстве ().

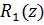Будем по определенному закону любой точке ставить в соответствие некоторое число 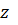из множества 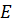: 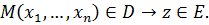Тогда говорят, что на множестве 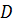определена однозначная функция 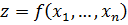от переменных 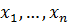. Область 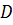называется областью определения функции 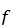, область 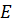называется областью значений функции 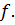Переменные 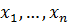называются независимыми переменными, переменная 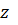называется зависимой переменной.

Рассмотрим основные определения.

Определение 1. Расстоянием между точками называется величина ρ

ρ.

Определение 2. 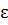– окрестностью точки называется множество :

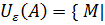ρ

Определение 3. – мерным шаром с центром в точке и радиусом 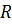назовем множество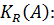

Определение 4. Проколотой 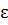– окрестностью точки называется множество :

.

Определение 5. Точка 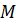называется внутренней точкой множества 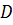, если (см. рис.).

Определение 6. Множество 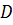называется открытым множеством, если все его точки являются внутренними.

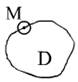Определение 7. Точка 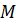называется граничной точкой множества 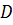, если любая окрестность точки содержит как точки множества 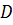, так и не принадлежащие .

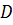Определение 8. Множество всех граничных точек 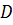называется границей множества .

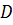Обозначим: - граница множества

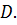
Определение 9. Точка 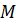называется предельной точкой множества 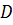(точкой сгущения), если любая окрестность точки 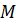содержит хотя бы одну точку множества .

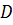Очевидно, что все граничные точки являются точками сгущения.

Определение 10. Множество, содержащее все свои предельные точки называется замкнутым.

Обозначим замкнутое множество: .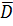

Пусть множество 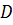является открытым. Операция присоединения всех предельных точек к множеству 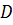называется замыканием множества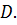

Определение 11. Пусть 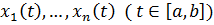– некоторые непрерывные функции. Множество точек , состоящее из точек , называется непрерывной кривой.

Будем говорить, что точки можно соединить непрерывной кривой , если существует такая непрерывная кривая , определяемая параметрическими уравнениями , что .

Определение 12. Область 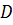называется связной, если любые две точки области 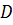можно соединить непрерывной кривой, все точки которой лежат в .

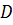Дата добавления: 2014-01-05