Метод Гаусса-Жордана

Наибольшая точность решения достигается тогда, когда ведущий элемент строки имеет наибольшее значение. Поэтому строку с нулевым или малым ведущим элементом на ту из стоящих под ней строк, в которой в том же столбце стоит элемент, имеющий наибольшее значение.

Отличие метода Гаусса-Жордана от метода Гаусса в том, что преобразованная матрица имеет диагональный вид и нет необходимости в обратном ходе.

Схема с выбором главного элемента.

Так же, как и в методе Гаусса-Жордана, добиваемся наибольшего значения ведущих элементов, но уже перестановкой не только уравнений, но и столбцов неизвестных со своими неизвестными.

При определителе системы не равном нулю всегда приводит к единственному решению и менее чувствительна к погрешностям округления.

Пусть дана система (1). Сначала добиваемся выполнения условий |a⁰₁₁|>=|a⁰_ij| путем перестановки в случае необходимости двух уравнений системы (1), а также двух столбцов неизвестных со своими коэффициентами, и соответствующей перенумерации коэффициентов и неизвестных. Найденный максимальный по модулю коэффициент называется первым главным элементом. Затем исключаем х₁согласно предыдущей схеме. Далее с полученной системой уравнений поступаем аналогично исходной (выбираем максимальный по модулю второй главный элемент и т.д.). Обратный ход выполняется также аналогично. Перейдя к первоначальной нумерации уже найденных неизвестных, получим решение заданной системы уравнений.

Итерационные методы решения СЛАУ

Для решения СЛАУ итерационными методами система уравнений (1) преобразуется к виду:

х₁ = (а_{1, n+1} – a₁₁x₁– a₁₂x₂–…– a_1nx_n) / a₁₁+ x₁,

х₂ = (а_{2, n+1} – a₂₁x₁– a₂₂x₂–…– a_2nx_n) / a₂₂+ x₂, (9)

…………………………………………………

х_n = (а_{n, n+1} – a_n1x₁– a_n2x₂–…– a_nnx_n) / a_nn+ x_n,

Задав столбец начальных приближений х⁰₁, х⁰₂, …, х⁰_n, подставим их в правые части системы (9) и вычислим новые приближения х¹₁, х¹₂, …, х¹_n, которые опять подставим систему и т.д. Таким образом, организуется итерационный процесс, который является обобщением метода простых итераций на системы уравнений:

х₁⁽^m+1) = j₁(х₁⁽^m), х₂⁽^m), …, х_n⁽^m)),

х₂⁽^m+1) = j₂(х₁⁽^m), х₂⁽^m), …, х_n⁽^m)), (10)

………………………………….

х_n⁽^m+1) = j_n(х₁⁽^m), х₂⁽^m), …, х_n⁽^m)),

Метод Якоби использует произвольно выбранные начальные приближения 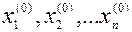для вычисления 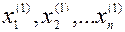и т.д. до тех пор, пока не будет достигнута точность, либо станет очевидно, что процесс расходится.

Эффективнее использовать метод Гаусса-Зейделя – прием последовательной подстановки уже вычисленных "новых" значений.

х₁⁽^m+1) = j₁(х₁⁽^m), х₂⁽^m), …, х_n⁽^m)),

х₂⁽^m+1) = j₂(х₁⁽^m+1), х₂⁽^m), …, х_n⁽^m)), (11)

………………………………….

х_n⁽^m+1) = j_n(х₁⁽^m+1), х₂⁽^m+1), …, х_n⁽^m)).

Для сходимости итерационных методов необходимо, чтобы значения диагональных элементов матрицы СЛАУ были преобладающими по абсолютной величине по сравнению с другими элементами. Условие сходимости можно обеспечить преобразованием исходной матрицы путем перестановки уравнений и неизвестных.

, (8)

Эти методы можно применять и к решению систем нелинейных уравнений. Итерационный процесс заканчивается, когда выполняется условие | х_k⁽^m+1) – х_k⁽^m)| < e, где e – заданная погрешность.

<== предыдущая лекция	\|	следующая лекция ==>
Формирование матричных уравнений состояния электрической цепи	\|	Применение ЭВМ для оптимального проектирования систем электроснабжения

Поделиться с друзьями:

Дата добавления: 2014-01-05; Просмотров: 1077; Нарушение авторских прав?; Мы поможем в написании вашей работы!

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

studopedia.su - Студопедия (2013 - 2025) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление

Генерация страницы за: 0.013 сек.