Применение ЭВМ для оптимального проектирования систем электроснабжения

(справочник по электроснабжению и электрооборудованию: В 2 т./ Под общ. ред. А. А. Федорова – М.: Энергоатомиздат, 1986, 568 с.)

Решение проектных и эксплуатационных задач промышленного электроснабжения связано с применением различных математических методов. На стадии проектирования инженер сталкивается с необходимостью решения задачи выбора схемы, конфигурации сети и ее элементов, а на стадии эксплуатации – повышения экономичности работы системы электроснабжения, т. е. оптимизации режима.

С точки зрения объема исходных данных для решения проектных и эксплуатационных задач современные системы электроснабжения можно отнести к классу больших систем с неполно заданной информацией. Поэтому в настоящее время разработаны и продолжают разрабатываться эффективные методы их расчета и оптимизации.

В задачах энергетики оптимизация — это стремление математически сформулировать наилучшие условия работы системы, пред­ставив их в виде целевой функции, и опреде­лить значения регулируемых параметров, со­ответствующих экстремальному значению целевой функции.

При оптимальном проектировании си­стем электроснабжения необходимо решить ряд задач. Основными из этих задач явля­ются:

1) выбор элементов систем электроснаб­жения (числа и мощности трансформаторов, сечений проводов, шин и жил кабелей и т. д.);

2) выбор основных параметров систем электроснабжения (электрических нагрузок, рационального напряжения);

3) определение оптимальной топологии электрической сети;

4) выбор режимов работы систем элек­троснабжения.

Цель оптимального проектирования си­стем электроснабжения может заключаться в снижении начальных капитальных или экс­плуатационных затрат, повышении надежно­сти проектируемой системы. Чаще всего это сокращение приведенных годовых затрат.

Если целевая функция задана алгорит­мически (конечным числом способов реали­зации решения), то оптимизацию сводят к простому перебору вариантов и выбору на­илучшего из них по известному критерию оптимальности. Такое решение возможно для задач с небольшим числом дискретных значений регулируемого параметра, напри­мер выбор рационального напряжения, сече­ния проводника. При большом числе возможных значений регулируемых параметров общее число вариантов оказывается значи­тельным, и даже с помощью ЭВМ решить задачу за приемлемый промежуток времени оказывается невозможным. В этом случае используют методы нахождения экстремума целевой функции F(x₁, х₂,..., х_n) (методы оптимизации).

В простейшем случае дифференцируемости целевой функции и неравенства нулю вторых производных задача сводится к ре­шению п алгебраических уравнений

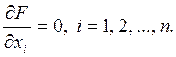(7)

В классической математике разработаны методы решения и доказательства принци­пиальной разрешимости уравнений вида (7), что привело к созданию так назы­ваемых аналитических методов оптимиза­ции. Из аналитических методов оптимизации в практике проектирования систем электро­снабжения широко применяют метод неопре­деленных множителей Лагранжа, отличаю­щийся простотой и наглядностью.

Сущность метода заключается в следую­щем. Пусть необходимо оптимизировать вы­пуклую целевую функцию от п переменных

F(x₁, х₂,..., х_n) (8)

Область допустимых решений опреде­ляется m уравнениями связи

ψ_j(x₁, х₂,..., х_n) = 0, j = 1, 2,..., т. (9)

Составляют вспомогательную функцию

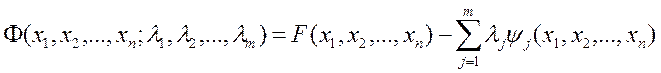(10)

где λ₁, λ₂, …, λ_m – неопределенные мно­жители Лагранжа. Необходимым условием существования экстремума функции (10) является равенство нулю ее частных про­изводных

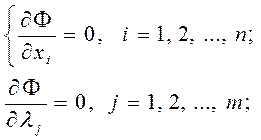(11)

Систему уравнений (11) преобра­зуют к виду

(12)

Решение п + т уравнений (12) относи­тельно п + т неизвестных дает искомые зна­чения переменных х,, х₂,..., х_п.

Метод неопределенных множителей Лагранжа эффективен при небольшом числе переменных и ограничений; с увеличением же числа переменных и ограничений на них сложность решения уравнений (12) резко возрастает. Поэтому наряду с аналитически­ми методами большое развитие получили методы линейного, нелинейного и динамиче­ского программирования. Реальные задачи математического программирования доста­точно сложны и, как правило, не могут быть решены без использования ЭВМ.

Математически задачу линейного про­граммирования ставят следующим образом: ищут минимум линейной формы

(13)

при соблюдении ограничений

(14)

Неравенства (13) можно свести к стро­гим равенствам, добавив переменную x_n+1:

(15)

Тогда условие (14) сводится к (15) и ус­ловию неотрицательности переменной x_n+1. Поэтому при решении задачи линейного программирования определяют такие значе­ния п переменных х, которые бы обращали в минимум линейную форму (13) при усло­вии выполнения m равенств (15).

Применение методов решения задачи линейного программирования в техни­ко-экономических расчетах систем электро­снабжения возможно, когда с относительно небольшой погрешностью нелинейные функ­ции затрат З_i от расчетной мощности S_pi на различные элементы сети могут быть ап­проксимированы линейными зависимостями вида

(16)

где b, с — постоянные коэффициенты для ка­ждой типовой группы элементов электриче­ской сети; m – число элементов схемы элек­троснабжения.

Линеаризация затрат позволяет полу­чить простую функцию цели (линейная функция от расчетной мощности) следующе­го вида:

.

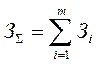В результате появляется возможность использовать для определения искомых оп­тимальных значений параметров хорошо разработанные методы решения задачи ли­нейного программирования, например сим­плекс-метод.

Методы решения задачи линейного про­граммирования достаточно подробно изла­гаются в соответствующей литературе. Разработаны также стан­дартные программы для решения подобных задач на ЭВМ.

Нелинейное программирование яв­ляется наиболее общей задачей математиче­ского программирования и включает в себя методы определения минимума функции п переменных

F(x₁, х₂,..., х_n) (17)

при m + п ограничениях

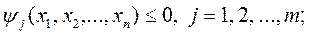(18)

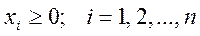(19)

В общем случае функции F(x₁, х₂,..., х_n) и ψ_j(x₁, х₂,..., х_n) бывают произвольными и, в частности, линейными. Допускают любые соотношения между п и т.

Задачи нелинейного программирования по сравнению с задачами линейного про­граммирования обладают большим разно­образием. Решение задач нелинейного про­граммирования может давать два или более экстремума. Теоретически наиболее широко и детально в нелинейном программировании разработан раздел квадратичного програм­мирования, т. е. для методов решения задач квадратичного программирования найдены соотношения, являющиеся необходимыми и достаточными условиями оптимума, и ал­горитмы поиска экстремума с доказатель­ством их сходимости. Функции (17), (18) в этом случае представляют в виде суммы линейной и квадратичной форм

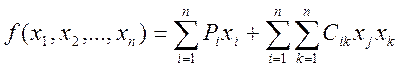(20)

Методы квадратичного программирова­ния применяют, например, для решения за­дач оптимального распределения реактивной мощности, так как потери активной мощно­сти являются квадратичной функцией реак­тивной мощности. В настоящее время нет универсальных методов решения задачи не­линейного программирования. В зависимо­сти от свойств целевой функции (17) и ограничений (18) эффективным может оказаться тот или иной метод. Сравнительная оценка методов и подбор наилучшего из них являются сложной задачей и во многом за­висят от опыта программиста, так как незна­чительная доработка алгоритма может суще­ственно повысить эффективность метода.

Основной недостаток методов нелинейного программирования заключается в том, что с их помощью не удается найти глобальный экстремум при наличии нескольких ло­кальных экстремумов. Определить гло­бальный экстремум можно лишь методом динамического программирования.

Метод наименьших квадратов

Пусть мы имеем экспериментальные данные, и нам необходимо провести аппроксимирующую кривую, которая не проходит через экспериментальные точки, но в то же время отражает исследуемую зависимость и сглаживает разброс значений за счет погрешности эксперимента. Применяется метод наименьших квадратов.

Имеем таблицу экспериментальных данных

хi	x1	x2	x3	xn
yi = f (xi)	y1	y2	y3	yn

Введем непрерывную функцию j (х) для аппроксимации дискретной зависимости f (x_i). В узловых точках функции j (х) и f (x) будут отличаться на величину e_i = j(x_i) – f (x_i). Отклонения e могут принимать положительные и отрицательные значения. Чтобы не учитывать знаки, возведем каждое отклонение в квадрат и просуммируем квадраты отклонений по всем узлам:

.

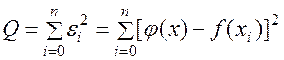Метод построения аппроксимирующей функции j(х) из условия минимума величины Q называется методом наименьших квадратов (МНК).

Далее: из условия Q' = 0 находятся неизвестные параметры.

Пример: парабола, линейная аппроксимация.

Динамическое программирование позволяет решать задачи, в которых процесс принятия решений может быть разбит на от­дельные этапы. При этом не имеет значения, протекает ли процесс во времени или пред­ставляет собой многошаговую формальную процедуру. Однако его применение зависит от определенных условий, обеспечивающих выполнение принципа оптимальности Беллмана.

Условия, при которых может быть при­менен метод динамического программирова­ния, следующие:

1) для рассматриваемой управляемой системы, которая под действием управления переходит из начального S₀ в конечное S_n со­стояние, состояние в конце k -го этапа S_k за­висит только от предшествующего состоя­ния S_k-1, и управления на данном этапе U_k. Это свойство получило название отсутствия последствия;

2) целевая функция должна быть адди­тивной, т. е. должна представлять собой сумму частных функций, рассчитанных на отдельных этапах:

.

Принцип оптимальности Беллмана мо­жет быть сформулирован следующим обра­зом: последующие решения должны соста­влять оптимальное поведение относительно предыдущего состояния, полученного в ре­зультате решения на предыдущем этапе, не­зависимо от того, какими бы эти состояние и решение ни были. Это положение в аналитической форме можно записать в виде следующего соотношения:

.

Динамическое программирование мож­но представить как некоторый оптимальный метод перебора вариантов. Это достигается за счет того, что на каждом этапе процесса рассматривают лишь оптимальное его пред­ложение. С помощью метода динамического программирования в настоящее время доста­точно эффективно решают задачи энергетики (например, оптимизация развития электриче­ских сетей, выбор варианта развития линий электропередачи, совместный выбор компен­сирующих и регулирующих устройств в си­стеме электроснабжения и др.).

Схемы замещения воздушных и кабельных линий электропередачи

(Герасименко А.А., Федин В.Т. Передача и распределение электрической энергии. – Ростов н/Д: Феникс, 2008.- 715 с.)

Дата добавления: 2014-01-05