Комплексные числа

Форма ведения плана и учета

На сегодня нет единой формы ведения плана (молодые - развернутый).

План составляется на день, неделю, 2 недели, месяц. Система занятий может разрабатываться на квартал, месяц, конкретизироваться в ежедневном плане.

В плане фиксируется:

1. Название занятия

2. Програмное содержание

3. Оборудование

4. План занятия

Література

1.Аршавский И.А. Физиология развития детей. - Пущино: Ин-т биофизики АН СССР, 1985. – 36 с.

2. Васин Ю.Г. Физические упражнения – основа профилактики ожирения у детей. – К.: Здоров’я, 1981. – 156 с.

3. Валеология и физическая реабилитация в учебно-воспитательной работе // Международный сборник научных работ. ХГИФК: -Белгород. – 1996. – 425 с.

4. Вільчковский Э.С. Теорія і методика фізичного виховання дітей дошкільного віку. Львів: ВНТЛ. - 1998. – 336 с.

5. Вильчковский Э.С. Развитие двигательной функции у детей. – К.: Здоров’я, 1983. – 208 с.

6. Кузьмина Н.В. Методы исследования педагогической деятельности. – Л.: ЛГУ, 1970. – 114 с.

7. Методичні рекомендації “Планування навчально-виховної роботи за експериментальною програмою формування культури здоров’я дітей дошкільного віку “Малятко - здоров’ятко” /Денисенко Н.Ф., Шевцова Л.Г., Паук С.Л та ін. – Запоріжжя, 2004. – 68с.

8. Поддъяков Н.Н. Мышление дошкольника. – М.: Педагогика. – 272 с.

9. Програма виховання дітей дошкільного віку. Малятко / Відпов.ред. Плохій З.П./. – К.: 1991. – 200 с.

10. Програма виховання і навчання дітей дошкільного віку. Дитина. /Відпов.ред. Проскура О.В./ К.: Освіта, 1993. – 272 с.

11. Программа учебного предмета «Основы здорового образа жизни» для общеобразовательной школы всех ступеней. – Запорожье, ЗГУ, 1993. – 28.

12. Ротенберг Р. Расти здоровым: Детская энциклопедия здоровья: Пер. с англ. – М: Фізкультура и спорт, 1992. – 592 с.

13. Рубинштейн С.Л. Бытие и сознание. – М.: Изд-во АН СССР, 1957. – 328с.

14. Русова С. Теорія педагогіки на основі психології. – Прага, 1924. – 234 с.

15. Савченко О.Я. Розвиток пізнавальної самостійності молодших школярів. – К., 1982. – 176 с.

16. Спок В. Ребенок и уход за ним: Пер.с англ.. – М.: Пресса, 1992. – 271 с.

17. Сухарев А.Г. Здоровье и физическое воспитание детей и подростков. – М.: Медицина, 1991. – 272 с.

18. Шмалей С.В. Діагностика здоров’я: Практическое пособие по оздоровлению. – Херсон, 1994. – 208с.

19. Формирование здорового образа жизни детей: Комплексный межотраслевой поход: // Метод.рекомендации/. – Алма-Ата, 1991. – 24 с.

Лекции на тему «Комплексные числа»

Понятие числа, которое является одним из самых основных математических понятий, имеет свою многовековую историю. Число, как и все научные понятия, возникло не в результате свободного творчества человеческого разума, а было создано для удовлетворения практических потребностей людей. Так как с течением времени практическая деятельность людей развивалась, то и понятие числа также изменялось и совершенствовалось.

Понятие о числе возникло в доисторические времена в связи с необходимостью счета различных предметов, животных, растений и т. д. Поэтому первоначально рассматривались лишь целые и положительные числа, которые теперь называют натуральными числами. Натуральные числа вполне удовлетворяли потребности практики тех времен, и лишь по прошествии многих веков возникли дробные числа как результат деления, производимого над объектами, для которых имеет смысл дробление единицы на равные доли. Потребность более точных измерений таких величин, как длина, площадь, вес, время и т. п., привела к дроблению основной единицы меры на более мелкие части, получившие особые наименования.

Так, например, были введены минута (от латинского minutus — уменьшенный, малый) для обозначения 1/60 часа или градуса, секунда (от латинского secunda — второй, т. е. второе деление) для обозначения 1/60 минуты, или 1/602 = 1/3600 часа или градуса.

Несмотря на то, что дробные числа встречаются в самых древних из известных нам рукописей, понятие дроби как отвлеченного числа проникало в науку с чрез­вычайным трудом и начало получать признание лишь в XVI—XVII веках после изобретения десятичных дробей и логарифмов. Особенно большие логические труд­ности представлял тот факт, что при умножении на правильную дробь в резуль­тате получалось число не большее, а меньшее исходного. Интересно также отметить, что еще Штифель в 1553 г. назвал дроби «воображаемыми числами».

Целые положительные числа совместно с числами дробными получили назва­ние рациональных чисел.

Задачи измерения непрерывных величин, т. е. выражения всякого значения такой величины числом, привели к введению чисел иррациональных.

Историческое предание приписывает так называемое «открытие» иррациональ­ных чисел Пифагору, который обнаружил несоизмеримость диагонали квадрата с его стороной. Другими словами, Пифагор обнаружил, что отношение длины диа­гонали квадрата к длине его стороны не может быть выражено никаким рацио­нальным числам (это отношение может быть выражено только бесконечной дробью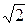: а : а = 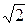= 1,414213...).

Значительно позже начали появляться и входить в обиход отрицательные числа. Систематическое применение отрицательных чисел в общих формулах и их исполь­зование в качестве коэффициентов алгебраических уравнений одновременно с вве­дением нуля как самостоятельного числа впервые встречаются у индусов (VI— XI век) и несколько позже у народов Средней Азии и Закавказья — хорезмийцев, таджиков, узбеков, азербайджанцев и др. Индусам же принадлежит и правильное истолкование нуля, отрицательных чисел и действий над ними на примерах прос­тейших направленных величин, таких как прибыль — убыток, перемещение в про­тивоположных направлениях и т. п.

В этом отношении средневековые европейские алгебраисты долгое время отста­вали от ученых Востока и либо совсем не рассматривали отрицательных решений уравнений, либо, получая такие уравнения, считали отрицательные числа фиктив­ными, абсурдными числами, «числами меньшими, чем ничто». Лишь в XVI веке Декарт, разрабатывая аналитическую геометрию, дал геометрическое истолкование отрицательных чисел как направленных отрезков, которое с тех пор и стало общепринятым.

Новое расширенное понятие о числе окончательно закрепляется в математике в самом начале XVIII века определением, данным Ньютоном, которое было при­ведено в конце § 24 гл. III.

Числа рациональные и иррациональные, положительные и отрицательные полу­чили общее название действительных, или вещественных, чисел.

Геометрически действительные числа изображаются точками числовой оси — прямой, на которой указано положительное направление, масштаб и начальная точка (т. е. точки, изображающие нуль и единицу).

Однако не успело еще закрепиться новое расширенное понятие числа, как в процессе дальнейшего развития математики обнаружилось, что и новое понятие является также неудовлетворительным. В частности, решение квадратных уравне­ний уже на самой ранней ступени развития алгебры привело к невозможной в области действительных чисел операции извлечения квадратного корня из отри­цательного числа.

Величина b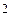 при любом числовом значении b будет не отрицательна, т. е. она может быть либо положительна, либо равна нулю, например при b = +8 имеем b 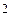= +64; при b = 0 и b 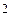= 0.

Таким образом, среди действительных чисел нет ни одного такого, квадрат которого был бы величиной отрицательной; следовательно, и корень квадратный из отрицательной величины 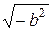не может быть выражен никаким действитель­ным числом.

Означает ли это, однако, что величина 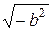является «воображаемой», «не­возможной», «мнимой», как ее называли, следуя традиции, неизменно повторяю­щейся при всяком новом расширении понятия числа?

Конечно, нет. Величина 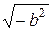является реально существующей величиной, которая только не может быть выражена узким, несовершенным понятием действи­тельного числа.

С аналогичными явлениями мы сталкиваемся не только в математике. Напри­мер, обыкновенная фотопленка всю красочность природы передает как комбинацию черных и белых тонов. Однако в связи с этим никто не утверждает, что «действи­тельными» цветами являются только белый и черный, а все остальные — «вообра­жаемые», «невозможные», «мнимые». Новая, более совершенная пленка, светочув­ствительный слой которой состоит не из одного, а из трех слоев, чувствительных соответственно к синему, желтому и зеленому цветам, уже в состоянии дать сни­мок в натуральных красках.

Так и в рассматриваемом случае, кроме известной «действительной» единицы, при помощи которой выражаются все действительные числа, необходимо ввести еще одну, принципиально новую единицу, которую будем обозначать буквой i, понимая под этим обозначением величину

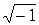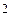i = или i= -1.

Тогда 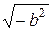может быть выражено через новую единицу i так:

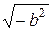= ib.

По исторической традиции число i назвали мнимой единицей, а числа ib - чисто мнимыми числами. Число вида a + ib получило название комплексного числа, в котором различают действительную часть (а) и мнимую часть (b).

Действительные числа, как было сказано выше, геометрически изображаются точками числовой оси. Комплексные числа на одной числовой оси представить невозможно. Они изображаются точками числовой плоскости: каждое конкретное комплексное число изображается точкой в системе прямоугольных координат. Осью абсцисс является действительная числовая ось, а осью ординат — ось «чисто мнимых чисел» Для изображения комплексных чисел на числовой плоскости необходимо уже задать начало отсчета (нулевую точку), положительное направление каждой из осей и две масштабные единицы: действительную (1) и мнимую (i). Обычно масштаб по обеим осям выбирают одинаковым, но это не является обязательным.

Таким образом, любому комплексному числу а + ib = (1 • а) + (i • b) соответствует одна и только одна точка числовой плоскости,

Установленный факт кратко формулируется так: между точками числовой плоскости и всем множеством комплексных чисел существует взаимно однозначное соответствие.

Комплексные числа начали появляться в работах отдельных математиков на­чиная с XVI века. Но широкое признание и распространение они получили лишь в XIX веке, после того как на рубеже XVIII — XIX веков одновременно и неза­висимо друг от друга К. Гауссом (в 17971799 гг.), К. Весселем (в 1798—1799 гг.) и Ж. Арганом (в 1806 г.) была дана геометрическая интерпретация комплексных чисел как точек числовой плоскости, и после того, как при помощи комплексных чисел удалось решить ряд практически важных задач, неразрешенных в области действительных чисел.

До тех пор к комплексным числам относились с большим недоверием и не понимали их сути даже многие крупные математики. Например, Лейбниц писал: «Комплексное число — это тонкое и поразительное средство божественного духа, почти амфибия между бытием и небытием».

В заключение остановимся еще на связи между расширением понятия числа и на возможностях выполнения математических действий.

В области натуральных чисел всегда выполнимы только сложение и умноже­ние. Вычитание уже может приводить к числам отрицательным, а деление — к дробным.

В области рациональных чисел всегда выполнимы все четыре действия арифме­тики, но действие извлечения корня не всегда возможно.

В области действительных чисел возникшая трудность снята лишь частично: извлечение корня возможно за исключением извлечения корней четной степени из отрицательных чисел.

В области комплексных чисел всегда выполнимы все четыре действия арифме­тики и извлечения корня любой степени из любого комплексного числа. (Действие возведения в степень мы не рассматриваем, так как оно эквивалентно действию умножения).

В результате выполнения этих действий над комплексными числами снова получаем комплексные числа.

Для комплексных чисел остаются справедливыми все основные законы ариф­метики и алгебры и в качестве значения функции от комплексного аргумента мы получаем снова комплексное число.

Кроме того, целый ряд вопросов, которые в области действительного перемен­ного не могли быть решены и часто рассматривались как парадоксы, получили простое и естественное объяснение в области комплексного переменного.

Например, в области комплексного переменного алгебраическое уравнение n-й степени всегда имеет точно n корней, в то время как в области действитель­ного переменного оно может иметь и меньшее число корней и даже ни одного.

В области комплексного переменного существует логарифм от отрицательных чисел, функции синус и косинус могут принимать любые значения, а не только значения, не превышающие единицы, и т. д.

Дата добавления: 2014-01-05