
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение, изображение комплексных чисел. Действия над комплексными числами в алгебраической форме
|
|
|
|
Комплексные числа
На множестве С вводятся понятия функции, предела таким образом, что соответствующие понятия действительного анализа рассматриваются как частный случай. Естественно, при этом сохраняются известные свойства функций действительного переменного: теоремы о пределах, правила дифференцирования, формулы интегрирования и т.д. Однако, благодаря расширению класса функций, частым случаем которых являются функции действительного переменного, появляются новые свойства. Например, доказывается, что из существования производной функции следует существование ее производных n-го порядка в области. Устанавливается, что все элементарные функции связаны между собой: тригонометрические функции выражаются через показательную функцию, а обратные тригонометрические - через логарифмическую. Значительно глубже, чем в анализе функций действительного переменного, развита геометрическая теория - конформные отображения. Благодаря сочетанию аналитических и геометрических методов теория функций комплексного переменного находит широкое применение в других разделах математики и прикладных задачах.
Комплексным числом z называется выражение вида
z = x + iy, где х и у – действительные числа, а i – так называемая мнимая единица, i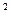 = -1.
= -1.
Если х = 0, то число 0 + iy = iy называется чисто мнимым; если у = 0, то число х + i0 = х отождествляется с действительным числом х. Число х называется действительной частью комплексного числа z и обозначается х = Re z, а у – мнимой частью z и обозначается у=Im z. Запись числа z в виде z = x + iy называют алгебраической формой комплексного числа.
Два комплексных числа Z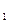 = x
= x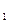 + iy
+ iy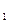 и Z
и Z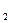 = x
= x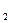 + iy
+ iy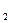 называются равными (Z
называются равными (Z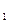 = Z
= Z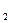 ) тогда и только тогда, когда равны их действительные части и их мнимые части: x
) тогда и только тогда, когда равны их действительные части и их мнимые части: x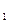 = x
= x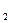 , y
, y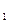 = y
= y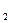 . В частности, комплексное число Z = x + iy равно нулю тогда и только тогда, когда х = = у = 0.
. В частности, комплексное число Z = x + iy равно нулю тогда и только тогда, когда х = = у = 0.
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Пример 1. При каких действительных значениях х и у выполняются равенства:
а) x (2 – i) + y (2i – 1) = 4 – 5i;
б) ix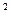 + (3 – i) x – (1 – 2i) y = 2 + 2i?
+ (3 – i) x – (1 – 2i) y = 2 + 2i?
3. Два комплексных числа z = x + iy и 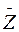 = x – iy, отличающиеся лишь знаком мнимой части, называются сопряженными.
= x – iy, отличающиеся лишь знаком мнимой части, называются сопряженными.
Например: 1 + i и 1 – i; 2i и –2i.
Комплексные числа, отличающиеся знаком действительной и мнимой частей, называются противоположными.
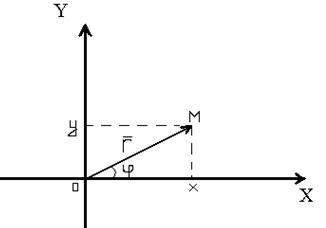
Всякое комплексное число z = x + iy можно изобразить точкой М(х;у) плоскости Оху такой, что x = Re z, y = Im z. Ось OX называется действительной, ось OY-мнимой. И, наоборот, каждую точку М(х;у) координатной плоскости можно рассматривать как образ комплексного числа z = x + iy. Комплексное число Z можно задавать с помощью радиус-вектора 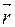 =
= 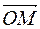 =
= 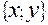 .
.
Пример 2. Изобразить геометрически следующие комплексные числа и им сопряженные: а) 3; б) 2i; в) –2-3i; г) 1 + 2i.
Длина вектора 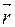 называется модулем комплексного числа и обозначается
называется модулем комплексного числа и обозначается  или r: r =
или r: r = 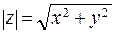 . Величина угла между положительным направлением действительной оси и вектором
. Величина угла между положительным направлением действительной оси и вектором 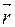 , изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Arg z или
, изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Arg z или 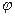 . Arg z = arg z + 2
. Arg z = arg z + 2 ,
,  - любое целое число; arg z – главное значение аргумента,
- любое целое число; arg z – главное значение аргумента,
- < arg z ≤ p. Аргумент
< arg z ≤ p. Аргумент 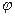 определяется из формулы:
определяется из формулы: 
 tg
tg 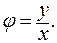
Так как 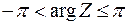 , то из формулы:
, то из формулы: 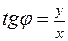 получаем, что
получаем, что


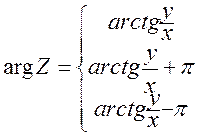
 Если точка z лежит на действительной или мнимой оси, то arg z можно найти непосредственно.
Если точка z лежит на действительной или мнимой оси, то arg z можно найти непосредственно.
Пример 3. Найдите модуль и главное значение аргумента следующих комплексных чисел: а) 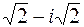 ; б) –3i.
; б) –3i.
Суммой двух комплексных чисел Z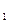 = x
= x + iy
+ iy и Z
и Z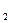 = x
= x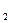 + iy
+ iy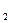 называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством 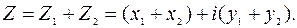
Свойства сложения комплексных чисел:
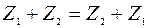
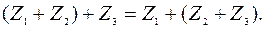
Вычитание определяется как действие, обратное сложению. Если  то
то 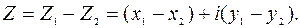
Произведением комплексных чисел Z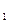 = x
= x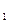 + iy
+ iy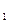 и Z
и Z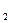 = x
= x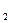 + iy
+ iy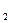 называется комплексное число, определяемое равенством:
называется комплексное число, определяемое равенством: 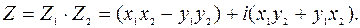 Заметим, что
Заметим, что 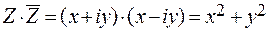 - действительное число.
- действительное число.
Свойства умножения комплексных чисел:

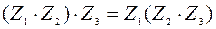
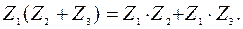
Например: 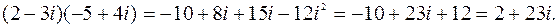
9. Деление определяется как действие, обратное умножению. Если
 то
то
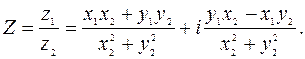
На практике частное двух комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю («избавляются от мнимости в знаменателе»).
2. Тригонометрическая и показательная формы комплексного числа
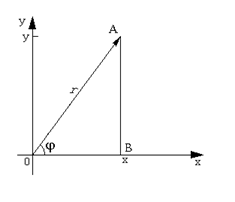 1. Рассмотрим комплексное число z в алгебраической форме:
1. Рассмотрим комплексное число z в алгебраической форме: 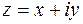 . Изобразим это число на комплексной плоскости в виде вектора
. Изобразим это число на комплексной плоскости в виде вектора 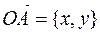 .Рассмотрим
.Рассмотрим 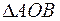 , где
, где 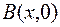 .
.
Пусть r - модуль комплексного числа z; 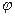 -один из его аргументов (любой). Тогда из
-один из его аргументов (любой). Тогда из 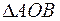 следует, что
следует, что 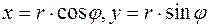 . Откуда число z запишется в виде:
. Откуда число z запишется в виде: 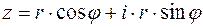 . Представление числа z в виде:
. Представление числа z в виде: 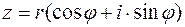 называется тригонометрической формой комплексного числа z.
называется тригонометрической формой комплексного числа z.
Пример 1. Представьте в тригонометрической форме комплексные числа 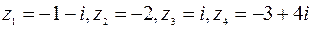 .
.
Пример 2. Записать числа в тригонометрической форме
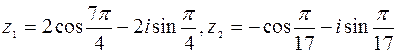
2. Пусть 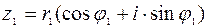 ,
,  ,
,
Тогда 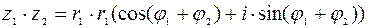 ,
,
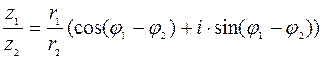 .
.
Пример 3. Найти произведение чисел
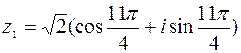 и
и 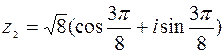 .
.
Пример 4. Записать в тригонометрической форме комплексное число 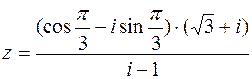 .
.
3. Пусть 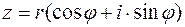 , тогда
, тогда 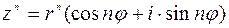 (формула Муавра), где
(формула Муавра), где 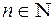 .
.
Пример 5. Вычислить. 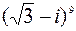 .
.
4. Корнем n-ой степени из комплексного числа z называется такое комплексное число W (обозначается 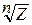 ), если
), если 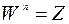 .
.
Все значения корня n-ой степени из 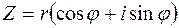 содержатся в формуле
содержатся в формуле
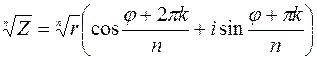 (1), где k=0,1,2,…,n-1.
(1), где k=0,1,2,…,n-1.
Пример 6.Найти все значения:
a) 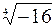 ; б)
; б) 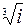 ; в)
; в) 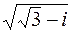 .
.
Пример 7. Записать число  в алгебраической форме при условии, что действительные части корней
в алгебраической форме при условии, что действительные части корней 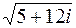 и
и 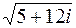 отрицательны.
отрицательны.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1258; Нарушение авторских прав?; Мы поможем в написании вашей работы!