Исследование линейных систем на фазовой плоскости

Особенности метода фазового пространства.

1. фазовые пространства и фазовые траектории это лишь геометр образы динамических процессов протекающих в системе. 2. в этом геометр-ом предствал-ии участвуют фазовые координаты, а время исключено. 3. Фазовая траектория дает лишь качественное но неколичественное представление о характере поведения системы. 4. Если исходная система ур-ий составлена в отклонениях от установившегося состояния, то установ-ся состояние будет харак-ся началом координат в фазовом пространстве. 4.1 Соотв-е фазовые траектории устойчив системы будут асимптотически приближаться к началу координат. 4.2 Для НС фазовые координаты в различных областях могут иметь различные очертания. 4.3 В верхней полуплоскости фазовой плоскости, фазовые точки с увелич времени всегда направлены в сторону возрастания координаты х1. Главное св-во фазов. траектории которое обуславливает наглядность фазового портрета состоит в том, что фазовые траектории никогда не пересекаются в не особых точках. Недостатки: 1) Сложность исследования систем выше II порядка. 2) Нет количественных оценок во времени.

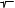
Постановка задачи: Пусть дана лин-я система которая описыв-ся ур-ем II порядка, где х-это отклонение от заданного состояния d²x/dt²+a₁dx/dt+a₀x=0 (1) Требуется построить фазовый портрет и исследовать систему на устойчивость качества при различ. элементах a₁, a₀. процедура исследования линейных систем на фазовой плоскости сост. из след. этапов: I. представление исходной системы в виде Коши (диф ур-е I порядка). Введем х=х1, тогда {^dx1/dt=x2_{dx2/dt=-a0x1-a1x2}; (2) dx₂/dt=d²x₁/dt² =d²x/dt². II. Состоит в исключение времени. Поделим второе ур-е на первое, чтобы исключить время. dx₂/dx₁= (-a₀x₁/x₂)– a₁ (3) III. Нахождение решения и построение фазовых траекторий, анализ устойчивости и качества. Вид фазовой траектории зависит от расположения корней хар-го ур-я в соотв-ии с необходимым и достаточным условием устойчивости. Запишем хар-ое ур-е для данной системы: p²+ a₁p+a₀=0 => p_1,2=-a₁/2 ± a₁²/4-a₀ (4). Рассмотрим все случаи: Iслуч когда а₁=0 а₀>0, исходя из представления ур-я (3) с учетом выше написанных коэфф-ов, запишем dx₂/dx₁= -a₀x₁/x₂, p_1,2=± -a₀=±j a₀, проинтегрируем: x₂dx₂=a₀x₁dx₁. x₂²/2= -a₀x₁²/2+C. x₂²/2C+x₁²/(2C/ a₀)=1 – уравнение элипса.

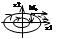Направление на фазовых траекториях определяем следующим образом: 1) выберем точку М₀ в I квадранте, для нее харак-но

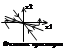х1>0, x2>0 => dx1/dx2>0; далее dx2/dx1=-a₀x₁ <0. Def Особая точка- на фазовой плоскости это такая точка в которой направление движения не определено. Для нас это особая точка типа центр. II случ а1>0, a0>0 => (a₁²/4)-a₀>0. p1=-α₁; p2=-α₂. Для этого случая мы можем записать решение в следующем виде: x₁=Σ²_i=1 c_ie^-αt, x₂=dx₁/dt=-Σ²_i=1 α_ic_ie^-αt.

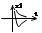
Затухающим апереодич. процесса соотв-ет фазовая траектория вливающаяся в начало координат. поскольку явно разделить переменные не удается (прим. ур-я 3), поэтому построение ведется с помощью следующей таблицы.

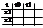Особая точка в данном случае называется устойчивый узел.

III случ а1<0, a0>0 =>(a₁²/4)-a₀>0. p1=α₁; p2=α₂.

x₁=Σ²_i=1 c_ie^αt, x₂=dx₁/dt=Σ²_i=1 α_ic_ie^-αt.

Мы наблюдаем следующий процесс. Он так же может протекать по разному:

IV случ a1>0, a0>0, (a₁²/4)-a₀<0; p₁,₂=-α±jβ.

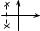x1=c₁e^-αtsin(βt+φ). Тогда производная равна x2=-αc₁e^-αtsin(βt+φ)+ βc₁e^-αtсos(βt+φ).

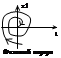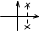
Особая точка типа устойчивый фокус. V случ: a1<0, a0<0, (a₁²/4)-a₀<0; p₁,₂=α±jβ. x1=c₁e^αtsin (βt+φ). x2=αc₁e^αtsin(βt+φ)+ βc₁e^αtсos(βt+φ).

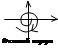Особая точка типа неустойчивый фокус.

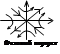VI случ: а1=0, а0<0; p₁,₂=±√-а₀=±ω₀. Пусть -а₀= ω₀². Исходя из dx₂/dx₁= (-a₀x₁/x₂)– a₁, получим dx₂/dx₁= -a₀x₁/x₂ => dx₂/dx₁= ω₀x₁/x₂; x₂dx₂=ω₀²x₁dx; x₂²/2= (ω₀²x₁²/2)+C; (x₀²/2C) – (x₁²/(2C/ω₀²))=1-гипербола.

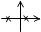
Особая точка называется типа седло.

Дата добавления: 2014-01-05