Исследование Н.С. на фазовой плоскости

Пусть дана система след. вида:

W₀(p)=z(p)/u(p)=k₀/p

W_ИМ(p)=u(p)/v(p)=k_И/p

Будем анализировать поведение системы в откланениях от заданного значения g=0 E=g-z=-z

v=f(E) описание НЭ-та

Этим передаточным функциям соотв-ют след. диф. уравнения:

dz/dt=k₀*u

du/dt=k_И*u (1)

Перепишем эти уравнения относительно ошибки E=-z

dE/dt=-k₀*u

du/dt=k_И*f(E)

u=-1/k₀*dE/dt

-1/k₀*d²E/dt²=k_И*f(E)

d²E/dt²=-k₀*k_И*f(E) (2)

Введем обозначение E=x₁

dE/dt=dx₁/dt=x₂

dx₂/dt=d²x₁/dt²=-k₀*k_И*f(x₁)

Проведем исследование:

1. Записываем систему уравнений в форме Коши:

dx₁/dt=x₂

dx₂/dt=-k₀*k_И*f(x₁)

2. Исключаем время (2)/(1)

dx₂/dx₁=-k₀*k_И*f(x₁)/x₂

Дальнейшее исследование проведем для различных характеристик НЭ:

1) f(x)=k*x₁

dx₂/dx₁=-k₀*k_И*k*x₁/x₂

x₂*dx₂=-k₀*k_И*k*x₁*dx₁

x₂²/2=-k₀*k_И*k*x₁²/2+c

k₀*k_И*k=K

x₂²/(2c/K)+x₂²/2c=1

Имеем незатухающие колебания.

Особая точка – типа центр.

2) НЭ – идеальное реле

V= k, x₁>=0

- k, x₁<0

dx₁/dt=x₂

dx₂/dt=-k₀*k_И*f(x₁)

f(x₁)= k, x₁>=0

-k, x₁<0

3.Определение линий перекл-ния

Линия кот. разбивает фаз. плоскость на области внутри кот. нелинейность имеет линейное значение наз. линией переключения.

4. Построение фаз. траекторий по облястям.

а) Пусть x₁>0, f(x₁)=k

dx₁/dt=x₂

dx₂/dt=-k₀*k_И*k

dx₂/dx₁=-k₀*k_И*k/x₂

x₂*dx₂=-k₀*k_И*k*dx₁

x₂*dx₂=-K*dx₁

x₂²/2=-K*x₁+c – ур-ние параболы

x₁>0

dx₂/dt=-K

б) Пусть x₁<0 f(x₁)=-k

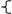dx₁/dt=x₂

dx₂/dt=k₀*k_И*k=K

dx₂/dx₁=K/x₂

x₂*dx₂=K*dx₁

x₂²/2=K*x₁+c – ур-е параболы

Объединяем оба участка

Фаз. траектории представляют собой две параболы с линией переключения на оси ординат. Траектория замкнутая.

Вывод: в системе возникают незатухающие негармонические автоколебания.

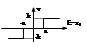3) реле с зоной нечувствительности

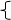k, x₁>a

V= 0, -a<=x₁<=a

-k, x₁<-a

3. Определение линий переключения

x₁=a, x₁=-a

4. Построение фаз. траектории по участкам

a) x₁>a v=+k (см. пред. случай)

x₂²/2=-K*x₁+c

б) x₁<-a v=-­k (см. пред. случай)

x₂²/2=K*x₁+c

в) –a<=x₁<=+a v=0

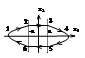
dx₁/dt=x₁

dx₂/dt=0

dx₂/dx₁=0

x₁=const

В системе устанавливаются гармонические колебания

Введение зоны нечувствительности приводит к появлению отрезков покоя и полосы образованной линиями переключения x₁=a, x₁=-a внутри которой отрезки фаз. траектории параллельны оси абсцис.

4) Стабилизируем систему введя местную ООС по скорости (коррекция по скорости)

НЭ – идеальное реле

dz/dt=k₀*u

du/dt=k_и*f(s)

g=0

E=g-z=-z

s=E-a*u

E= x₁

dE/dt=x₂

u=1/k₀*dz/dt=-1/k₀*dE/dt=

=-1/k₀*dx₁/dt

3. Линия переключения s=0

E-a*u=0 E=x₁ u=1/k₀*x₂

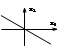x₁+a/k₀*x₂=0 – ур-е линии пер-ния

x₂=-k₀/a/*x₁

a) s>0 v=k

dx₁/dt=x₂

dx₂/dt=-k₀*k_и*k=-K

x₂²/2=-K*x₁+c

б) s<0 v=-k

dx₁/dt=x₂

dx₂/dt=+K

x₂²/2=+K*x₁+c

В системе возникают затухающие колебания.

Интересный случай возникает, когда касательная к фазовой траектории совпадает с линией переключения. В этом случае в системе возникает так называемое скольжение.

Отрезок АВ соответствует зоне, где существует скольжение.

Исходя из s=0, a*x₂+k₀*x₁=0 можем записать a*dx₂/dt+k₀*x₁=0

a*p+k₀=0, p=-k₀/a

x₁=c₁*exp(-k₀/a*t) (*)

По отрезку АВ происходит скольжение в соответствии с (*).

Найдем координаты т. А, где парабола касается линии переключения.

Из уравнения линий переключения

???-> x₂/x₁=-k₁/a далее

dx₂/dx₁=-k₀*k_и*k/x₂ Это в том случае, когда НЭ представлен как идеальное реле.

dx₂/dx₁=-k₀/a -k₀/a=-k₀*k_и*k/x₂

x₂=k_и*k*a отсюда найдем x₁

x₁=-a*x₂/k₀=-a²*k_и*k/k₀

Т.о. мы нашли координаты т.А.

По анологии находятся к-ты т.В.

Крайние точки отрезка скольжения АВ определяются как точки, в которых парабола касается правого и левого семейства. Внутри отрезка АВ фаз. тр-ии подходят к нему с двух сторон встречаясь в нем. Попав в этот отрезок изображающая точка не может сойти с него как и остаться на нем, поэтому она будет скользить по отрезку к началу координат. Однако точное движение (*) по линии скольжения невозможно в реальных условиях, т.к. оно может иметь место только при мгновенном срабатывании реле. Не мгновенность приводит к появлению замыканий и размыканий контактов большой частоты, может быть обгорание контактов. С появлением бесконтактных реле проблема снята и скользящие режимы стали создавать искусственно с целью обеспечения заданного качества.

Дата добавления: 2014-01-05