Исследование устойчивости нелинейных систем.Исследование НС с помощью метода Ляпунова

Основные понятия и определения в теории устойчивости.

Определение понятия устойчивости любой механической системы по Ляпунову:

Пусть уравнение динамики НС будет записано следующим образом y=F(y,t), пусть у^*(t)-движение по наперёд заданной траектории.

Отклонение движения y(t) определяется по уравнению 1, обозначим x(t)=y(t)-y^*(t), тогда отклонение х' =Ф(x, t), хÎR^N, движение по наперёд заданной траектории можно записать х^*=0, при этом xi, i=1,n можно рассматривать как переменное состояние системы.

Геометрическая интерпретация определения устойчивости по Ляпунову:

Невозмущённое движение системы х^* =0 называется устойчивым по Ляпунову, если задав трубу сколь угодно малого сечения Е можно подобрать в начальный момент времени t0 такую область начальных условий б(Е), что в дальнейшим с увеличением времени возмущённое движение x(t) не выйдет из заданной трубки Е.

Аналитическая формулировка.

Невозмущённое движение системы х^*=0 называется устойчивым по Ляпунову, если любого сколь угодно малого положительного числа Е существует такое сколь угодно малое б(Е), что êхi(t) ê< б(E,t0) i=1,n всегда выполняется условие êхi(t) ê<Е. Если кроме того, что система устойчива по Ляпунову выполняется предельное соотношение вида: lim x(t)=0 при t à к бесконечности, то невозмущённое движение системы х^* =0 называется асимптотически устойчивым по Ляпунову.

Понятие о знакоопределённых, знакопостоянных и знакопеременных функциях.

Функция V(x1,x2…xn) называется знакоопределённой функцией если во всей рассматриваемой области, содержащей нач. коорд. Она сохраняет один и тот же знак и обращается в 0 только в нач. коорд. Если n=3, то V=ax1² +bx2² +cx3². Знакоопределённые функции могут быть как положительно определёнными, так и отрицательно определёнными. Если функция V сохраняет один и тот же знак, но обращается в 0 не только в нач. коорд., то такая функция называется знакопостоянной. Например: n=3 V=ax1² +bx2² V=(x1+x2)² +x3²

Функция V называется знакопеременной, если она в рассматриваемой области не сохраняет свой знак. n=3 V=x1+x2+x3 Функция Ляпунова – это однозначная непрерывная функция, аргументами которой являются n координат состояния и которая в достаточно большой окрестности пространства состояний вокруг точки равновесного состояния системы является всегда положительной, имеет непрерывные частные производные и в равновесном состоянии системы принимает min значение. V(0)=min, V(0)=0. Пусть динамика системы описывается: dxi/dt=Ф(x1 …xn) (1) dx/dt=Ф(x). Берём функцию Ляпунова V(х1….хn) Рассмотрим производную по времени в силу исходных уравнений (1): dV/dt=¶V/¶x1*dx1/dt+¶V/¶2*dx2/dt+…..+¶V/¶xn*dxn/dt В результате подстановки из системы (1) получим dV/dt=¶V/¶x1*Ф1+ ¶V/¶2 * Ф2+ …..+¶V/¶xn*Фn gradV={¶V/¶x1, ¶V/¶2,…., ¶V/¶xn}. С другой стороны вектор скоростей, изображающий точку можно представить как Ф={ dx1/dt, dx2/dt,…., dxn/dt } Фn=gradV, Ф=½grad V½*½Ф½* cosj (2) 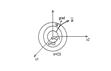Представили функцию Ляпунова в виде поверхности равного уровня. Вектор gradV перпендикулярен поверхности. Если dV/dt>0, то согласно выражению (2) вектор Ф составляет с gradV острый угол, т. е. фазовая траектория пересекает поверхность V=const в сторону увеличения значения V. Если dV/dt<0, то угол тупой и фазовая траектория идёт в сторону уменьшения значения V.

12 1-ая теорема 2-го метода Ляпунова (об устойчивости).

Теорема Если для системы 1 существует знакоопределённая функция V(x), производная которой по времени dV/dt в силу ур-ний 1 является знакопостоянной противоположного знака, то решение системы устойчиво.

Геометрическая интерпретация:

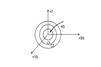dV/dt<0, то фазовая траектория пересекает поверхности уровня из вне- внутрь

dV/dt=0, то фазовая траектория может остаться на такой поверхности.

Дата добавления: 2014-01-05