Приближенные методы исследования НС. Метод гармонической линеаризации при симметричных колебаниях

Основу метода гармонической линеаризации составляют следующие исходные предположения. Пусть имеется НС 1 класса и нелинейная статическая характеристика y = F(x). Линейная часть Wлч(p) = R(p) / Q(p) m / n

Предполагается, что на вход Н звена подается гармонический сигнал x = a sin wt = a sin i (1).

Следовательно на выходе y = F (a sin wt) (2). Этот периодический выходной сигнал нелинейного звена можно разложить в ряд Фурье:

A0 n

y = —— + Σ (An cos n wt + Bn sin n wt) (3)

2 j = 1

где нужно определиться с коэффициентами:

w 2π / w

A0 = —— ∫ F (a sin wt) dt /

π 0 /

w 2π / w /

An = —— ∫ F (a sin wt) cos n wt dt / (4)

π 0 /

w 2π / w /

Bn = —— ∫ F (a sin wt) sin n wt dt /

π 0 /

Из условий физической реализуемости предполагается, что порядок числителя меньше порядка знаменателя (m ≤ n), т. е. срабатывает фильтр низких частот.

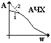
1 – статистическая система

2 – астатизм. Допускаем, что в данной системе возможны автоколебания и предполагаем соответственно, что линейная часть обладает свойством фильтра низких частот A(nw) << A(w), где n = 2, 3… При наличии фильтра линейная часть будет хорошо пропускать только первую гармонику нелинейных колебаний (3) и ослаблять все высшие гармоники. Таким образом, задача сводится к представлению существенно нелинейной зависимости в более простом виде, с учетом фильтра низких частот ЛЧ, а именно к проведению гармонической линеаризации существенной нелинейности. Таким образом, из выражения (3) ограничиваемся только первыми гармониками. Тогда y = (A0 / 2) + A1 cos wt + B1 sin wt (5). Для симметричных колебаний А0 = 0. Введем некоторый коэффициент q(a) = B1/a и q'(a) = A1/a. Получили: y = q '(a) a cos wt + q(a) a sin wt (6) A0 = 0, т. к. симметричные колебания. x = a sin wt dx / dt = aw cos wt d / dt = p => px = aw cos wt

y = q '(a) (px/a) + q(a)x y = (q (a) + q '(a) p / w) x (7)

2π/w

q(a) = B1/a = w/πa ∫ F(a sin wt) sin wt dt

0 wt = i 0 ≤ t ≤ 2π/w 0 ≤ i ≤ 2π q(a) = —1/2па ∫^2п₀ F (a sin i) sin i di (8)

q'(a) = A1/a = w/π a ∫^2п₀ F (a sin wt cos wt) dt q'(a) = 1/π a = ∫^2п₀ F (a sin i) cos i dt (9)

Представление (7) называется гармонической линеаризацией нелинейности, а коэффициенты q(a) и q' (a) – ее коэффициентами. Когда амплитуда постоянна – правая част выражения (7) линейна. Если зависимость F(x) не имеет гистерезиса, то коэффициент q' (a) = 0 и тогда зависимость (7) упрощается и получается y = q(a) x (10). Т.е. криволинейная или ломаная зависимость y = F(x) с точностью до высших гармоник заменяются прямолинейной характеристикой, tg угла наклона зависит от амплитуды колебаний а. При гистерезисе коэффициент q' (a) не равен 0, в следствии различия в очертании нелинейности при возрастании и убывании аргумента коэф. q (a) и q' (a). Пусть дана нелинейная характеристика следующего вида:

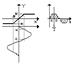
x1 = a sin i1 = b sin i1 = b/a i1 = arcsin b/a

При вычислении коэф гармонической линеаризации для симметричных колебаний можно

2π 2π

∫ = ∫ а для симметричных относительно

0 0 начала координат без гистерезисных

характеристик, при вычислении q(a) можно 2π

2π π/2 ∫ = 4 ∫

0 0

0 0

/ kx/b, x ≤ b, x ≥ b

F(x) = / k, x > b

/ -k, x < - b

q(a) = 4/πa ∫^2п₀ F (a sin ψ) sinψdψ = 4/πa[∫^ψ1₀ F (a sin ψ) sin ψ dψ + ∫^п/2_ψ1 F (a sin ψ)sin ψdψ ] =

= 4/πa [∫^ψ1₀ (k/b) a sin²ψdψ + ∫^п/2_ψ1 ksinψdψ] = (4/πa) · (ka/b) ∫^ψ₀ ((1-cos2ψ) / 2) dψ – (4k/πa) cosψ |= (2k/πb) ψ1 – 0 - (2k/πb2) sin 2ψ |_ψ1^ψ2 - 0 + (4k/πa) cosψ1 = (2k/πb) [ arcsin (b/a) – ((2 sinψ1 cosψ1) / 2) + (2b/a) √ 1 – b/a] = (2k/πb) [ arcsin b/a - b/a √ 1 – b²/a² + 2b/a √ 1 – b²/a²]

q(a) = 2k/πb [ arcsin b/a + b/a √ 1 – b²/a² ]

Дата добавления: 2014-01-05