Аннулирующий многочлен

Ортогональная классификация поверхностей второго порядка.

Ортогональная классификация кривых второго порядка

Приведение квадрики ортогональным преобразованием. Ортогональные инварианты и полуинварианты.

Рассмотрим задачу упрощения уравнения квадрики с использованием ортогональным преобразованием системы координат. Отметим, что при ортогональной замене координат сохраняются метрические характеристики.

Опишем алгоритм приведения квадрики к простейшему виду ортогональным преобразованием.

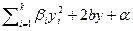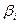1. Приводим квадратичную форму к главным осям ортогональным преобразованием . В результате получим уравнение квадрики , где , k – ранг матрицы A, а - ее ненулевые собственные числа.
2. Сдвигом начала координат при и при i > k приведем квадрику к виду , где . Если при i > k, то конец, а иначе перейдем на следующий шаг.
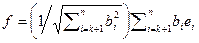3. Положим . Система векторов 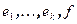- ортонормированная. Дополним ее до ортонормированного базиса всего пространства. Пусть T – матрица перехода к новому базису. Сделаем замену переменных 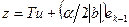. Очевидно, сделанная замена является ортогональной. В новой системе координат уравнение квадрики .

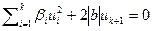Оформим доказанное выше в виде теоремы.

Теорема 9.2. Ортогональным преобразованием, сдвигом начала координат и умножением на ненулевое число уравнение квадрики приводится к одному из следующих четырех видов , , , .

Обозначим через 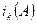сумму всех главных миноров k -го порядка матрицы A. Величина 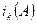является коэффициентом характеристического многочлена 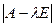при .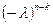

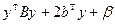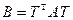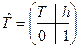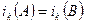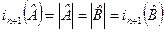Пусть квадрика ортогональным преобразованием x = h + Ty приводится к виду , где , , . Поскольку T ортогональная матрица, то , и, значит, , где k= 1,…, n. Кроме того, , и, следовательно, . Тем самым установлен следующий факт.

Свойство 9.1 При ортогональном преобразовании не меняются следующие величины 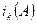, где k= 1,…, n, и , которые называются ортогональными инвариантами квадрики.

К сожалению, ортогональные инварианты не всегда позволяют установить простейший тип квадрики.

Свойство 9.2. Пусть 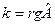и , тогда 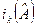не меняется при ортогональном преобразовании.

Доказательство. При ортогональном преобразовании (без сдвига) величины 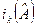не меняются. Пусть квадратичная форма приводится к главным осям ортогональной заменой координат 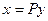. Пусть - ортогональное преобразование квадрики. Поскольку 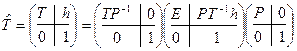, то для доказательства утверждения достаточно рассмотреть случай, когда 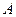- диагональная матрица и преобразование заключается в сдвиге на вектор h начала координат. Если 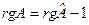, то . В этой матрице единственный минор k порядка, не содержащий нулевых строк, определитель которого не зависит от сдвига. Следовательно, утверждение в данном случае доказано. Пусть , тогда 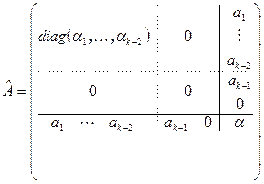. В этой матрице единственный минор k порядка, не содержащий нулевых строк, определитель которого не зависит от сдвига. Следовательно, утверждение и в данном случае доказано.

Величины 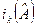называются полуинвариантами ортогонального преобразования.

Набор инвариантов и полуинвариантов квадрики позволяет однозначно установить простейшее уравнение квадрики.

Теорема 9.3. Любая кривая второго порядка ортогонально эквивалентна одному из 9 классов кривых, приведенных в таблице. Приведенные кривые ортогонально не эквивалентны между собой.

Название кривой	Каноническое уравнение кривой
Эллипс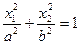
Мнимый эллипс
Гипербола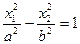
Пара пересекающихся мнимых прямых
Пара пересекающихся прямых	,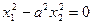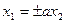
Парабола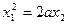
Пара параллельных прямых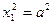
Пара параллельных мнимых прямых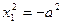
Пара совпавших параллельных прямых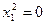

Доказательство. очевидно

Теорема 9.4 Любая поверхность второго порядка ортогонально эквивалентна одной из поверхностей в одном из 17 классов, приведенных в таблице. Приведенные поверхности ортогонально не эквивалентны между собой.

Название поверхности	Каноническое уравнение поверхности
Эллипсоид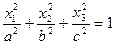
Мнимый эллипсоид
Однополостный гиперболоид
Двуполостный гиперболоид
Мнимый конус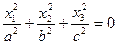
Конус
Эллиптический параболоид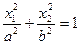
Эллиптический цилиндр
Мнимый эллиптический цилиндр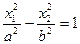
гиперболический цилиндр
Пара пересекающихся мнимых плоскостей	,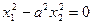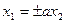
Пара пересекающихся плоскостей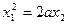
Параболический цилиндр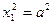
Пара параллельных плоскостей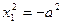
Пара параллельных мнимых плоскостей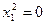
Пара совпавших плоскостей
Гиперболический параболоид (седло)

Доказательство очевидно.

Дата добавления: 2014-01-05