
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 5. § 128. Эллипсоид
|
|
|
|
Аналитическая геометрия.
Глава 9. Поверхности второго порядка, заданные каноническими уравнениями
Определение. Эллипсоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид: 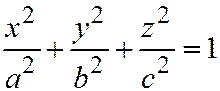 (1)
(1)
Будем считать, что 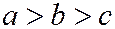 . Если на эллипсоиде лежит точка
. Если на эллипсоиде лежит точка 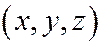 , то на нём лежат и точки
, то на нём лежат и точки  (с любым набором знаков плюс или минус). Отсюда следует, что для эллипсоида (1) начало координат
(с любым набором знаков плюс или минус). Отсюда следует, что для эллипсоида (1) начало координат  является его центром симметрии и называется центром эллипсоида; оси координат являются осями симметрии и называются главными осями; плоскости координат являются плоскостями симметрии и называются главными плоскостями.
является его центром симметрии и называется центром эллипсоида; оси координат являются осями симметрии и называются главными осями; плоскости координат являются плоскостями симметрии и называются главными плоскостями.
Если 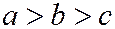 , то эллипсоид называется трёхосным.
, то эллипсоид называется трёхосным.
Если 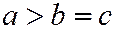 , то эллипсоид называется вытянутым эллипсоидом вращения; он получается вращением эллипса:
, то эллипсоид называется вытянутым эллипсоидом вращения; он получается вращением эллипса: 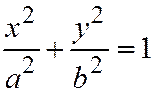 вокруг его большей оси (См. рис. 197)
вокруг его большей оси (См. рис. 197) 
Если  , то эллипсоид называется сжатым эллипсоидом вращения; он получается вращением эллипса:
, то эллипсоид называется сжатым эллипсоидом вращения; он получается вращением эллипса: 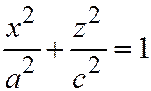 вокруг его малой оси (См. рис. 198)
вокруг его малой оси (См. рис. 198)
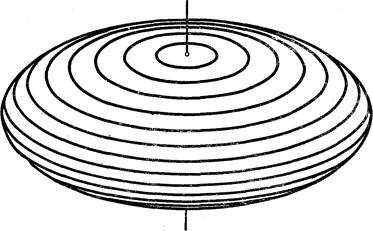
Рис. 198.
Если  , тоэллипсоид является сферой радиуса
, тоэллипсоид является сферой радиуса 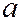 с центром в начале координат.
с центром в начале координат.
Вершинами трёхосного эллипсоида являются точки пересечения эллипсоида с его главными осями. Трёхосный эллипсоид имеет 6 вершин 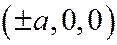 ,
,  ,
,  .
.
Из уравнения (1) следует, что 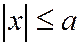 ,
, 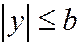 ,
,  . Это означает, что эллипсоид (1) лежит внутри прямоугольного параллелепипеда с вершинами
. Это означает, что эллипсоид (1) лежит внутри прямоугольного параллелепипеда с вершинами  . Каждая грань этого параллелепипеда имеет с эллипсоидом только одну общую точку - его вершину.
. Каждая грань этого параллелепипеда имеет с эллипсоидом только одну общую точку - его вершину.
Плоскость  пересекает эллипсоид (1) по линии, выраженной уравнениями:
пересекает эллипсоид (1) по линии, выраженной уравнениями: 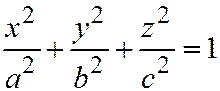 ,
,  или эквивалентной системой:
или эквивалентной системой:  (2)
(2)
Аналогично плоскость  пересекает эллипсоид (1) по линии, уравнения которой:
пересекает эллипсоид (1) по линии, уравнения которой:  ,
, 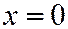 , (3) а плоскость
, (3) а плоскость  по линии:
по линии:  ,
,  . (4)
. (4)
Линии (2), (3), (4) суть эллипсы. Эти эллипсы, т.е. сечения эллипсоида (1) его главными плоскостями, называются главными сечениями.
Рассмотрим сечения эллипсоида какими-нибудь координатными плоскостями, например плоскостями, параллельными плоскости 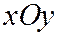 , т.е. плоскостями, выраженными уравнением
, т.е. плоскостями, выраженными уравнением 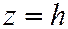 , где
, где  - произвольное действительное число. В таком случае, уравнения линии сечения имеют вид:
- произвольное действительное число. В таком случае, уравнения линии сечения имеют вид: 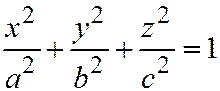 ,
, 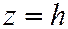 , или
, или 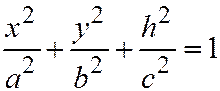 ,
, 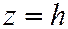 , или:
, или:  (5) Если
(5) Если 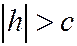 , то первому уравнению системы (5) не удовлетворяет ни одна пара действительных чисел
, то первому уравнению системы (5) не удовлетворяет ни одна пара действительных чисел 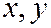 т.е. система (5) не имеет действительных решений
т.е. система (5) не имеет действительных решений  . это означает, что плоскость
. это означает, что плоскость 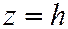 при
при 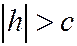 не пересекает эллипсоид (1).
не пересекает эллипсоид (1).
При  первое уравнение системы (5) имеет вид:
первое уравнение системы (5) имеет вид:  , откуда
, откуда  . Таким образом, плоскости
. Таким образом, плоскости 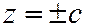 встречают эллипсоид (1) в его вершинах
встречают эллипсоид (1) в его вершинах 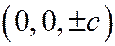 . Наконец, если
. Наконец, если 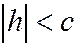 , то систему уравнений (5), выражающих линию сечения, можно переписать так:
, то систему уравнений (5), выражающих линию сечения, можно переписать так: 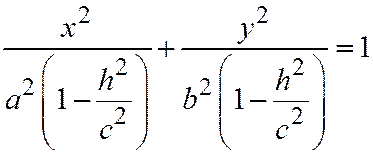 ,
, 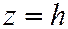 .
.
Или:  ,
, 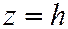 .
.
Эти уравнения являются уравнения эллипса, лежащего в плоскости сечения 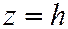 ; центр этого эллипса - точка
; центр этого эллипса - точка 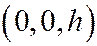 , оси симметрии параллельны осям
, оси симметрии параллельны осям 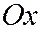 и
и 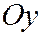 , а полуоси равны:
, а полуоси равны: 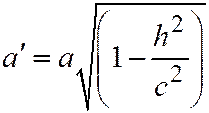 ,
, 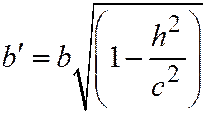 . Таким образом, любое сечение эллипсоида плоскостями, параллельными координатным, дают в сечении эллипс.
. Таким образом, любое сечение эллипсоида плоскостями, параллельными координатным, дают в сечении эллипс.
Отметим, что эллипсоид (1) может быть получен из сферы 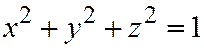 , если провести 3 равномерных сжатия:
, если провести 3 равномерных сжатия:  ;
;  ;
;  к трём попарно перпендикулярным плоскостям.
к трём попарно перпендикулярным плоскостям.
§ 129. Однополостный гиперболоид
Определение. Однополостным гиперболоидом на-зывается поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе коор-динат, имеет вид:  (6)
(6)
Будем считать, что  . Также как и в преды-дущем параграфе доказывается, что для однополостного гиперболоида (6) начало координат является центром симметрии (центр однополостного гиперболоида). Оси координат являются осями симметрии (главные оси), а координатные плоскости - плоскостями симметрии (главные плоскости) (См. рис. 200).
. Также как и в преды-дущем параграфе доказывается, что для однополостного гиперболоида (6) начало координат является центром симметрии (центр однополостного гиперболоида). Оси координат являются осями симметрии (главные оси), а координатные плоскости - плоскостями симметрии (главные плоскости) (См. рис. 200).
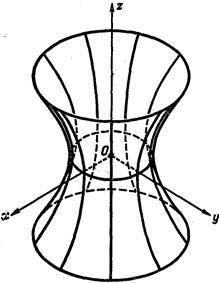
Рис. 200.
Если в уравнении (6)  , то однополостный гиперболоид (6) называется однополостным гиперболоидом вращения, так как может быть получен вращением гиперболы
, то однополостный гиперболоид (6) называется однополостным гиперболоидом вращения, так как может быть получен вращением гиперболы  вокруг мнимой оси (См. рис. 200).
вокруг мнимой оси (См. рис. 200).
Вершинами однополостного гиперболоида называ-ются точки пересечения гиперболоида с его главными осями. Гиперболоид (6) в случае 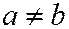 имеет 4 вершины
имеет 4 вершины 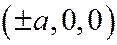 ;
;  .
.
Плоскость  пересекает однополостный гипер-болоид (6) по эллипсу, выраженному уравнениями:
пересекает однополостный гипер-болоид (6) по эллипсу, выраженному уравнениями:
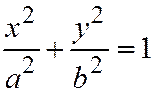 ,
,  , называемому горловым эллипсом однополостного гиперболоида (6). Плоскость
, называемому горловым эллипсом однополостного гиперболоида (6). Плоскость  пересекает однополостный гиперболоид (6) по гипер-боле, выраженной уравнениями:
пересекает однополостный гиперболоид (6) по гипер-боле, выраженной уравнениями:  ,
, 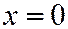 .
.
А плоскость  пересекает однополостный гиперболоид (6) по гиперболе, выраженной уравнениями:
пересекает однополостный гиперболоид (6) по гиперболе, выраженной уравнениями:  ,
,  .
.
Рассмотрим сечения однополостного гиперболоида (6) плоскостями, параллельными координатной плоскости 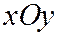 , т.е. плоскостями
, т.е. плоскостями 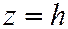 . Уравнения линии сечения будут:
. Уравнения линии сечения будут:  ;
; 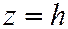 . Эта система уравнений эквивалентна следующей системе:
. Эта система уравнений эквивалентна следующей системе: 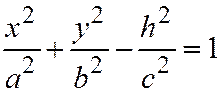 ;
; 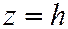 или
или
 ;
; 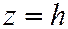 .
.
Этими уравнениям выражается эллипс с полуосями  ,
, 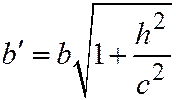 с центром на оси
с центром на оси  в точке
в точке 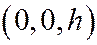 и осями, параллельными соответственно осям
и осями, параллельными соответственно осям 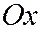 и
и 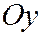 . из выражений
. из выражений  ,
, 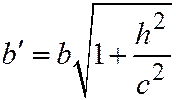 следует, что
следует, что  ,
,  , т.е. горловой эллипс является наименьшим из всех эллипсов, по которым однополостный гиперболоид (6) рассекается плоскостями, параллельными плоскости
, т.е. горловой эллипс является наименьшим из всех эллипсов, по которым однополостный гиперболоид (6) рассекается плоскостями, параллельными плоскости  .
.
Плоскость  , параллельная плоскости
, параллельная плоскости  , пересекает однополостный гиперболоид (6) по линии, выражаемой уравнениями:
, пересекает однополостный гиперболоид (6) по линии, выражаемой уравнениями:  ;
;  . Или
. Или  ;
;  .
.
Если 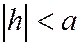 , то этими уравнениями определяется гипербола с центром в точке
, то этими уравнениями определяется гипербола с центром в точке  , лежащая в плоскости
, лежащая в плоскости  , действительная ось которой параллельна оси
, действительная ось которой параллельна оси 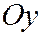 , а мнимая - оси
, а мнимая - оси  . Полуоси этой гиперболы:
. Полуоси этой гиперболы: 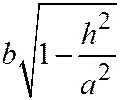 (действительная полуось),
(действительная полуось),  - (мнимая полуось).
- (мнимая полуось).
Если  , то уравнения линии сечения имеет
, то уравнения линии сечения имеет
вид:  ;
;  . Уравнения
. Уравнения  ;
; 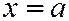 являются уравнениями двух пересекающихся прямых
являются уравнениями двух пересекающихся прямых  и
и 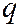 :
: 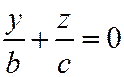 ,
, 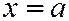 - прямая
- прямая  ;
;  ,
, 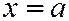 - прямая
- прямая 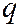 .
.
Аналогично уравнения  ;
;  являются уравнениями двух пересекающихся прямых:
являются уравнениями двух пересекающихся прямых: 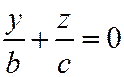 ,
,  и
и  ,
,  .
.
Если  , то в сечении получается гипербола, уравнения которой:
, то в сечении получается гипербола, уравнения которой:  ;
; 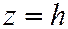 .
.
Действительная ось этой гиперболы параллельна оси  , мнимая - оси
, мнимая - оси 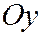 , центр лежит в точке
, центр лежит в точке  .
.
Асимптоты всех гипербол, получающихся при пересечении однополостного гиперболоида (6) плоскостями  ,
, 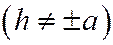 параллельны прямым, получающимся при пересечении гиперболоида плоскостями
параллельны прямым, получающимся при пересечении гиперболоида плоскостями  .
.
Сечения плоскостями 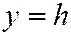 , параллельными плоскости
, параллельными плоскости  аналогичны рассматриваемым. Все эти сечения дают представление о форме поверхности однополостного гиперболоида (См. рис. 201).
аналогичны рассматриваемым. Все эти сечения дают представление о форме поверхности однополостного гиперболоида (См. рис. 201).

Рис. 201.
Всякий однополостный гиперболоид можно получить из однополостного гиперболоида вращения:  ,
, 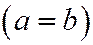 производя равномерное сжатие
производя равномерное сжатие 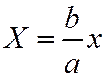 .
. 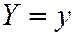 ,
,  к плоскости
к плоскости  . Однополостный гиперболоид (6) можно получить из равностороннего гиперболоида вращения:
. Однополостный гиперболоид (6) можно получить из равностороннего гиперболоида вращения:
 , производя равномерные сжатия
, производя равномерные сжатия  ,
,  ,
,  соответственно к плоскостям
соответственно к плоскостям  ,
,  и
и 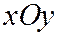 с коэффициентами сжатия
с коэффициентами сжатия 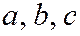 .
.
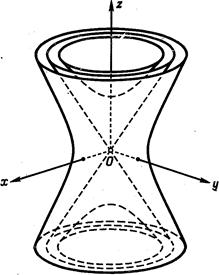
§ 130. Двуполостный гиперболоид.
Определение. Двуполостным гиперболоидом назы-вается поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе коор-динат, имеет вид:  . (7)
. (7)
Начало координат является центром симметрии (центр) двуполостного гиперболоида. Оси координат - осями симметрии (главные оси), координатные плос-кости - плоскостями симметрии (главные плоскости).
Если в уравнении (7)  , то двуполостный гиперболоид называется гиперболоидом вращения, так как может быть получен вращением гиперболы:
, то двуполостный гиперболоид называется гиперболоидом вращения, так как может быть получен вращением гиперболы:  вокруг его действительной оси (См. рис.
вокруг его действительной оси (См. рис.  202).
202).

Рис. 202. Рис. 203
Вершинами двуполостного гиперболоида называются точки его пересечения с главной осью  . Двуполостный гиперболоид (7) имеет две вершины
. Двуполостный гиперболоид (7) имеет две вершины  .
.
Плоскости  и
и  пересекает двуполостный гиперболоид (7) по гиперболам:
пересекает двуполостный гиперболоид (7) по гиперболам:  ,
,  , и
, и 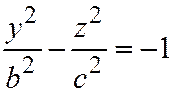 ,
, 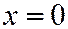 .
.
Сечения двуполостного гиперболоида (7) плоскостью 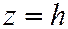 выражается уравнениями:
выражается уравнениями:
 ;
; 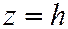 .
.
Если 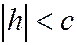 , то первое уравнение не имеет действительных решений - плоскость
, то первое уравнение не имеет действительных решений - плоскость 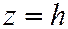 не пересекает поверхности.
не пересекает поверхности.
Если  , то
, то  , откуда
, откуда  , т.е. это две точки
, т.е. это две точки  .
.
Если 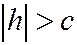 , то уравнение линии пересечения можно переписать в виде:
, то уравнение линии пересечения можно переписать в виде:
 ;
; 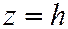 .
.
Этими уравнениями выражается эллипс с полуосями  ,
,  с центром в точке
с центром в точке 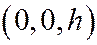 и осями, соответственно параллельными осям
и осями, соответственно параллельными осям 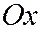 и
и 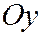 .
.
Плоскость  пересекает поверхность двуполостного гиперболоида (7) по линии, выражаемой уравнениями:
пересекает поверхность двуполостного гиперболоида (7) по линии, выражаемой уравнениями: 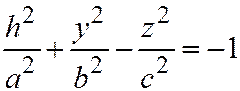 ;
;  .
.
Или  ;
;  ,
,
т.е. по гиперболе с центром в точке  , лежащей в плоскости
, лежащей в плоскости  . Действительная ось этой гиперболы, параллельна оси
. Действительная ось этой гиперболы, параллельна оси  , мнимая - оси
, мнимая - оси 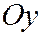 .
.
Аналогично исследуются сечения поверхности (7) плоскостями 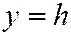 (См. рис. 203).
(См. рис. 203).
Двуполостный гиперболоид можно получить из двуполостного гиперболоида вращения:  ,
, 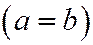 производя равномерное сжатие
производя равномерное сжатие 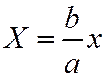 .
. 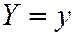 ,
,  к плоскости
к плоскости  . Двуполостный гиперболоид (7) можно получить из равностороннего двуполостного гиперболоида враще-ния:
. Двуполостный гиперболоид (7) можно получить из равностороннего двуполостного гиперболоида враще-ния:  , производя равномерные сжатия
, производя равномерные сжатия  ,
,  ,
,  соответственно к плоскостям
соответственно к плоскостям  ,
,  и
и 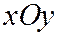 с коэффициентами сжатия
с коэффициентами сжатия 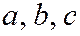 .
.
§ 131. Конус второго порядка.
Определение. Конусом второго порядка называется поверхность, уравнение которой в некоторой спе-циально выбранной прямоугольной системе коор-динат, имеет вид:  . (8)
. (8)
Считаем, что в этом уравнении  . Начало координат, оси координат и координатные плоскости являются соответственно, центром симметрии, осями симметрии и плоскостями симметрии и называются вершиной, главными осями и главными плоскостями.
. Начало координат, оси координат и координатные плоскости являются соответственно, центром симметрии, осями симметрии и плоскостями симметрии и называются вершиной, главными осями и главными плоскостями.
Осью конуса (8) обычно называют ось  . Основное свойство конуса - это, если на конусе лежит точка
. Основное свойство конуса - это, если на конусе лежит точка  (не совпадающая с вершиной), то на нём лежат все точки прямой
(не совпадающая с вершиной), то на нём лежат все точки прямой 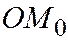 , проходящей через вершину
, проходящей через вершину  и эту точку
и эту точку 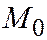 .
.
В самом деле, если 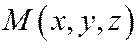 - произвольная точка, лежащая на прямой
- произвольная точка, лежащая на прямой 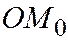 , то
, то 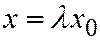 ,
,  ,
,  и поэтому:
и поэтому:
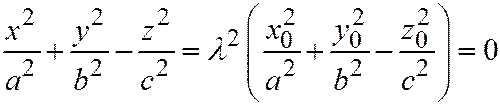 .
.
Таким образом, поверхность (8) образована прямыми, проходящими через начало координат. Поэтому для представления вида этой поверхности достаточно рассмотреть её сечение какой-нибудь плоскостью 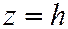 , параллельной плоскости
, параллельной плоскости 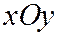 . В сечении получится эллипс, уравнения которого имеют вид:
. В сечении получится эллипс, уравнения которого имеют вид:  ,
, 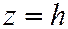 . Центр этого эллипса
. Центр этого эллипса  лежит на оси
лежит на оси  в точке
в точке 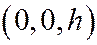 , а значит, поверхность (8) образована прямыми, соединяющими начало ко-ординат со всеми точками эллипса
, а значит, поверхность (8) образована прямыми, соединяющими начало ко-ординат со всеми точками эллипса  . (См. рис. 204).
. (См. рис. 204).
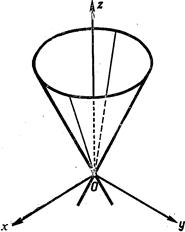
Рис. 204.
Конус (8) может быть получен в результате равномерного сжатия 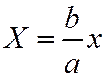 ,
, 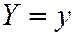 ,
,  к плоскости
к плоскости  конуса вращения
конуса вращения  , полученного вращением вокруг оси
, полученного вращением вокруг оси  прямой
прямой 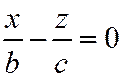 ,
,  , или в результате равномерного сжатия к плоскостям
, или в результате равномерного сжатия к плоскостям  ,
,  и
и 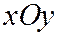 :
:  ,
,  ,
,  равностороннего конуса вращения
равностороннего конуса вращения 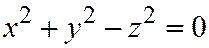 .
.
§ 131. Асимптотический конус гиперболоидов.
Два гиперболоида (один однополостный, другой двуполостный):  (9)
(9)
называются сопряжёнными.
Конус второго порядка, выражаемый уравнением:  (10)
(10)
называется асимптотическим конусом для обоих гиперболоидов.
Докажем, что любая плоскость, проходящая через ось  , пересекает поверхности (9) по сопряжённым гиперболам, а асимптотический конус (10) по двум прямым, которые для этих сопряженных гипербол являются асимптотами. В самом деле, повернём оси координат вокруг оси
, пересекает поверхности (9) по сопряжённым гиперболам, а асимптотический конус (10) по двум прямым, которые для этих сопряженных гипербол являются асимптотами. В самом деле, повернём оси координат вокруг оси  на угол
на угол 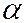 .
.
Уравнения (9) и (10) в новой системе координат 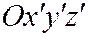 будут иметь вид:
будут иметь вид:
 , (
, (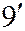 )
)
 . (
. ( )
)
Сечения этих поверхностей плоскостью  выражаются уравнениями:
выражаются уравнениями:
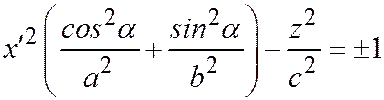 ,
, 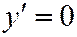 (
( )
)
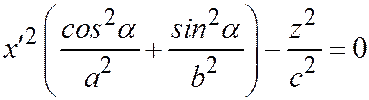 ,
, 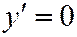 (
(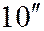 )
)
Из этих уравнений видно, что сечениями являются две гиперболы ( ) с полуосями:
) с полуосями: 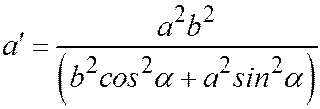 ,
, 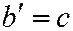 , а прямые (
, а прямые (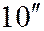 ) - асимптотами этих гипербол (См. рис. 205).
) - асимптотами этих гипербол (См. рис. 205).
Заметим, что все гиперболоиды семейства:  имеют общий асимптотический конус:
имеют общий асимптотический конус:  (См. рис. 206).
(См. рис. 206).

Рис. 205. Рис. 206.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 630; Нарушение авторских прав?; Мы поможем в написании вашей работы!