
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 6. § 133. Эллиптический параболоид
|
|
|
|
Аналитическая геометрия.
Глава 9. Поверхности второго порядка, заданные каноническими уравнениями
Определение. Эллиптическим параболоидом назы-вается поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе коор-динат, имеет вид:  , (1)
, (1)
где 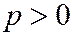 ,
,  . Будем считать, что
. Будем считать, что  . Если
. Если  , то эллиптический параболоид (1) является параболоидом вращения, т.к. получается вращением параболы:
, то эллиптический параболоид (1) является параболоидом вращения, т.к. получается вращением параболы:  вокруг оси
вокруг оси 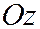 , являющейся осью параболы.
, являющейся осью параболы.
Ось 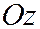 является осью симметрии эллиптического параболоида (1) (она называется осью параболида), а плоскости
является осью симметрии эллиптического параболоида (1) (она называется осью параболида), а плоскости 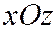 и
и  - плоскостями симметрии (главные плоскости). Начало координат для эллиптического параболоида (1) является точкой пересечения этой поверхности с её осью и называется вершиной.
- плоскостями симметрии (главные плоскости). Начало координат для эллиптического параболоида (1) является точкой пересечения этой поверхности с её осью и называется вершиной.
Плоскость  пересекает эллиптический парабо-лоид (1) по линии:
пересекает эллиптический парабо-лоид (1) по линии:  ,
,  ; или
; или
 ,
,  ; (2)
; (2)
Если 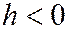 , то первое уравнение не имеет действительных решений, т.к.
, то первое уравнение не имеет действительных решений, т.к. 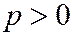 ,
,  , это означает, что плоскость
, это означает, что плоскость  при
при 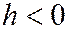 не пересекает эллиптический параболоид (1),
не пересекает эллиптический параболоид (1),
Если 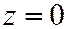 , то
, то  , т.е. плоскость
, т.е. плоскость 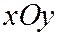 имеет с эллиптическим параболоидом только одну общую точку - вершину
имеет с эллиптическим параболоидом только одну общую точку - вершину  .
.
Если 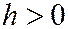 , то переписав уравнение (2) в виде:
, то переписав уравнение (2) в виде:
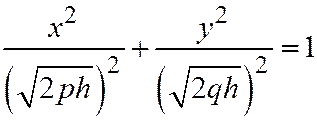 ,
,  , видим, что сечением является эллипс с центром в точке
, видим, что сечением является эллипс с центром в точке 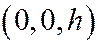 и полуосями:
и полуосями: 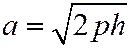 и
и 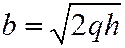 .
.
Плоскость 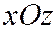 пересекает эллиптический параболоид (1) по параболе
пересекает эллиптический параболоид (1) по параболе  ,
, 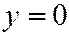 , а плоскость
, а плоскость  по параболе
по параболе  ,
, 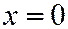 .
.
Таким образом, числа 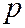 и
и  - параметры парабол, получающихся в сечении параболоида плоскостями симметрии (См. рис. 207).
- параметры парабол, получающихся в сечении параболоида плоскостями симметрии (См. рис. 207).

Рис. 207. Рис. 208.
Рассмотрим сечения эллиптического параболоида плоскостями, параллельными плоскостям 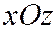 , т.е. плоскостями, выражаемыми уравнением
, т.е. плоскостями, выражаемыми уравнением  .
.
Уравнение линии сечения будет следующим:
 ,
,  , или
, или 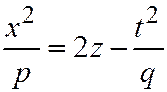 ,
,  , или:
, или:
 ,
,  .
.
Эти уравнения выражают параболу с вершиной  , ось которой выражается уравнением:
, ось которой выражается уравнением: 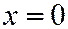 ,
,  и одинаково направлена с осью
и одинаково направлена с осью 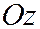 . Параметр параболы
. Параметр параболы  ,
,  равен
равен 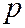 , т.е. параметру главного сечения эллиптического параболоида плоскостью
, т.е. параметру главного сечения эллиптического параболоида плоскостью 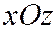 .
.
Аналогичная картина получается и для сечений эллиптического параболоида (1) плоскостями, параллельными плоскости  .
.
Таким образом, эллиптический параболоид может быть образован параллельным переносом параболы 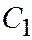 по параболе
по параболе  , а оси этих парабол параллельны и одинаково направлены (См. рис. 208).
, а оси этих парабол параллельны и одинаково направлены (См. рис. 208).
Эллиптический параболоид является образом параболоида вращения  при равномерном сжатии пространства:
при равномерном сжатии пространства:  ,
,  ,
, 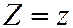 к плоскости
к плоскости  (коэффициент сжатия
(коэффициент сжатия 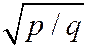 ).
).
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 469; Нарушение авторских прав?; Мы поможем в написании вашей работы!