
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные определения. Системы координат и базисы
|
|
|
|
Системы координат и базисы
Основные свойства операций над векторами
1) (a + b) + c = a + (b + c) (ассоциативность сложения);
2) a + b = b + a (коммутативность сложения);
3) a + 0 = 0 + a = a (существование нейтрального элемента по сложению);
4) a + (− a) = (− a) + a = 0 (существование противоположного элемента);
5) (λ + m) a = λ a + m a;
6) λ(a + b) = λ a + λ b;
7) (λm) a = λ(m a) (ассоциативность умножения на скаляр);
8) 1∙ a = a.
Свойства 5 и 6 в совокупности называются дистрибутивностью, свойство 8 специального названия не имеет. Свойства 1, 3 и 4 были доказаны выше, 2 было предоставлено читателю. Свойство 8 совершенно очевидно, доказательство свойств 5, 6 и 7 предоставляю читателю.
Хотя помимо приведённых восьми свойств, называемых основными, можно сформулировать множество других (некоторые из них сейчас будут приведены и доказаны), однако эти 8 свойств играют ту важную роль, что в принципе любое другое свойство можно чисто логически вывести из этих основных свойств, не опираясь на геометрию.
Примеры. 1. 0∙ a = 0.
Доказательство. 0∙ a = (0 + 0)∙ a = 0∙ a + 0∙ a;
0∙ a + (−(0∙ a)) = (0∙ a + 0∙ a) + (−(0∙ a));
0 = 0∙ a + (0∙ a + (−(0∙ a)));
0 = 0∙ a + 0;
0 = 0∙ a, QED.
Вы, конечно, можете сказать, что гораздо проще доказать это утверждение, обратившись непосредственно к определению умножения вектора на скаляр. Это так, но я хотел на этом примере показать, как можно выводить разнообразные свойства чисто логически из восьми основных.
2. λ∙ 0 = 0.
Доказательство. λ∙ 0 = λ(0 + 0) = λ∙ 0 + λ∙ 0;
λ∙ 0 + (−(λ∙ 0)) = (λ∙ 0 + λ∙ 0) + (−(λ∙ 0));
0 = λ∙ 0 + (λ∙ 0 + (−(λ∙ 0)));
0 = λ∙ 0 + 0;
0 = λ∙ 0, QED.
3. λ(a − b) = λ a − λ b (дистрибутивность умножения относительно вычитания).
Доказательство. Достаточно доказать, что
λ(a − b) + λ b = λ a.
Но действительно,
λ(a − b) + λ b = λ((a − b) + b) = λ a.
4. (λ − m) a = λ a − m a (дистрибутивность).
Доказательство. Достаточно доказать, что
(λ − m) a + m a = λ a.
Но действительно,
(λ − m) a + m a = ((λ − m) + m) a = λ a.
5. Если λ a = 0, то λ = 0 или a = 0.
Доказательство. В самом деле, пусть λ a = 0. Если λ ≠ 0, то
a = 1∙ a = (λ−1λ) a = λ−1(λ a) = λ−1∙ 0 = 0, QED.
А теперь мы в состоянии доказать единственность λ в формулировке предложения о двух параллельных векторах:
Предложение. Если a || b и b ≠ 0, то существует такое λ Î R, что a = λ b. Более того, это число (скаляр) λ определяется единственным образом.
Доказательство единственности. Пусть a = λ b и вместе с тем a = m b. Тогда
0 = λ b − m b = (λ − m) b,
откуда λ − m = 0 или b = 0. Но по условию предложения b ≠ 0, так что λ − m = 0, т. е. λ = m, QED.
Определение 1. Базисом в двумерном пространстве (т. е. на плоскости) называется любая пара неколлинеарных векторов.
Определение 2. Базисом в трёхмерном пространстве называется любая тройка некомпланарных векторов.
Определение 3. Стандартным базисом в двумерном пространстве (т. е. на плоскости) называется пара (неколлинеарных) векторов e 1, e 2, из которых первый есть вектор единичной длины, коллинеарный оси абсцисс и сонаправленный с нею, а второй есть вектор единичной длины, коллинеарный оси ординат и сонаправленный с нею. Обыкновенно будем представлять себе эти векторы приложенными к началу координат.
Определение 4. Стандартным базисом в трёхмерном пространстве называется тройка (некомпланарных) векторов e 1, e 2, e 3, из которых первый есть вектор единичной длины, коллинеарный оси абсцисс и сонаправленный с нею, второй есть вектор единичной длины, коллинеарный оси ординат и сонаправленный с нею, а третий есть вектор единичной длины, коллинеарный оси аппликат и сонаправленный с нею. Обыкновенно будем представлять себе эти векторы приложенными к началу координат.
Предложение 1. Пусть a, b − базис плоскости, т. е. пара неколлинеарных векторов. Тогда любой третий вектор c этой же плоскости может быть разложен по этому базису, т. е. представлен в виде линейной комбинации векторов a и b. Это означает, что найдутся такие числа λ и m, что имеет место равенство:
c = λ a + m b.
Более того, коэффициенты λ и m определяются единственным образом.
Доказательство. Приведём векторы a, b и c к общему началу S и пусть a = 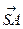 , b = =
, b = =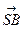 , c =
, c = 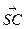 . Проведём через точку C прямую, коллинеарную вектору b, до пересечения с линией вектора a в точке P. (Эта прямая не может быть коллинеарна вектору a, т. к. в противном случае векторы a и b были бы коллинеарны.) Имеем:
. Проведём через точку C прямую, коллинеарную вектору b, до пересечения с линией вектора a в точке P. (Эта прямая не может быть коллинеарна вектору a, т. к. в противном случае векторы a и b были бы коллинеарны.) Имеем:
c = 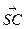 =
= 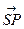 +
+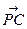 .
.
Т. к. 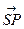 || a, а
|| a, а 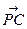 || b, то по предложению о двух коллинеарных векторах
|| b, то по предложению о двух коллинеарных векторах 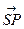 = λ a, а
= λ a, а 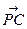 = = m b для некоторых чисел λ и m. Существование разложения доказано.
= = m b для некоторых чисел λ и m. Существование разложения доказано.
Для доказательства единственности предположим, что
λ1 a + m1 b = λ2 a + m2 b.
Тогда
λ1 a − λ2 a = m2 b − m1 b;
(λ1 − λ2) a = (m2 − m1) b.
Если λ1 ≠ λ2, то a =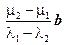 , и векторы a и b коллинеарны, что противоречит условию. А если λ1 = λ2, то (m2 − m1) b = 0, а т. к. b ≠ 0 (векторы a и b неколлинеарны), то m2 = m1, QED.
, и векторы a и b коллинеарны, что противоречит условию. А если λ1 = λ2, то (m2 − m1) b = 0, а т. к. b ≠ 0 (векторы a и b неколлинеарны), то m2 = m1, QED.
Предложение 2. Пусть a, b, c − базис трёхмерного пространства, т. е. тройка некомпланарных векторов. Тогда любой четвёртый вектор d может быть разложен по этому базису, т. е. представлен в виде линейной комбинации векторов a, b и c. Это означает, что найдутся такие числа λ, m и n, что имеет место равенство:
d = λ a + m b + n c.
Более того, коэффициенты λ, m и n определяются единственным образом.
Доказательство. Приведём векторы a, b, c и d к общему началу S и пусть a = 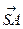 , b =
, b = 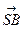 , c =
, c = 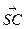 , d =
, d =  . Обозначим через π плоскость, проведённую через векторы a и b. Эта плоскость определяется однозначно, ибо векторы a и b неколлинеарны (иначе тройка a, b, c была бы компланарной). Проведём через точку D прямую, коллинеарную вектору c, до пересечения с плоскостью π в точке P. (Эта прямая не может быть параллельна плоскости π или лежать в ней, т. к. в противном случае вектор c лежал бы в ней, и векторы a, b, c были бы компланарны.) Имеем:
. Обозначим через π плоскость, проведённую через векторы a и b. Эта плоскость определяется однозначно, ибо векторы a и b неколлинеарны (иначе тройка a, b, c была бы компланарной). Проведём через точку D прямую, коллинеарную вектору c, до пересечения с плоскостью π в точке P. (Эта прямая не может быть параллельна плоскости π или лежать в ней, т. к. в противном случае вектор c лежал бы в ней, и векторы a, b, c были бы компланарны.) Имеем:
d =  =
= 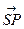 +
+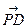 .
.
Т. к. 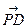 || c, то по предложению о двух коллинеарных векторах
|| c, то по предложению о двух коллинеарных векторах 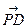 = n c для некоторого числа n. Что же касается вектора
= n c для некоторого числа n. Что же касается вектора 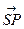 , то он лежит в плоскости π, и по предыдущему предложению может быть представлен в виде:
, то он лежит в плоскости π, и по предыдущему предложению может быть представлен в виде:
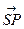 = λ a + m b.
= λ a + m b.
Существование разложения доказано.
Для доказательства единственности предположим, что
λ1 a + m1 b + n1 c = λ2 a + m2 b + n2 c.
Тогда
n1 c − n2 c = λ2 a − λ1 a + m2 b − m1 b;
(n1 − n2) c = (λ2 − λ1) a + (m2 − m1) b.
Если n1 ≠ n2, то c =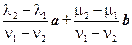 , и вектор c лежит в плоскости π, т. е. a, b, c компланарны, что противоречит условию. А если n1 = n2, то
, и вектор c лежит в плоскости π, т. е. a, b, c компланарны, что противоречит условию. А если n1 = n2, то
λ1 a + m1 b = λ2 a + m2 b,
и по предыдущему предложению λ1 = λ2, m2 = m1, QED.
Определение 5. Координатами вектора a называются (однозначно определённые) коэффициенты в разложении его по стандартному базису. Первая координата называется абсциссою и обозначается absc. a. Вторая координата называется ординатою и обозначается ord. a. Третья координата называется аппликатою и обозначается appl. a.
Определение. Координатами точки M (абсциссой, ординатой и аппликатой) называются соответствующие координаты вектора 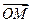 (где O − начало координат).
(где O − начало координат).
Таким образом, по определению
absc. M = absc. 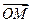 ;
;
ord. M = ord. 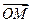 ;
;
appl. M = appl. 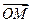 .
.
Если 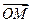 = {λ; m; n}, то M = (λ; m; n) (так обозначаем координаты точки M).
= {λ; m; n}, то M = (λ; m; n) (так обозначаем координаты точки M).
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 564; Нарушение авторских прав?; Мы поможем в написании вашей работы!