Основная теорема

Прямая линия на плоскости и плоскость в пространстве

Рассмотрим общий вид линейного уравнения (т. е. уравнения первой степени) в трёхмерном пространстве:

Ax + By + Cz + D = 0 (1)

и на плоскости:

Ax + By + C = 0. (2)

Обозначим через n вектор { A; B; C } (в двумерном случае { A; B }).

Основная теорема. Если n ≠ 0, то уравнение (1) является уравнением плоскости, а уравнение (2) − прямой линии. При этом вектор n ортогонален этой плоскости или пря­мой.

Доказательство буду вести для трёхмерного случая, для двумерного рассуждение аналогично.

Обозначим через Γ множество всех тех и только тех точек пространства, коорди­наты которых удовлетворяют уравнению (1). Нам надо доказать, что Γ есть плоскость, перпендикулярная n.

Убедимся прежде всего, что множество Γ непусто. Хотя бы одно из чисел A, B и C не равно 0. Пусть, например, B ≠ 0. (Для других случаев рассуждение аналогично.) Будем искать точку (x ₀; y ₀; z ₀), удовлетворяющую уравнению (1) и дополнительным условиям x ₀ = 0 и z ₀ = 0. Получаем уравнение

By ₀ + D = 0,

которое имеет (единственное) решение 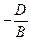, потому что B ≠ 0. Следовательно, точка (0; 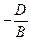; 0) Î Γ и Γ непусто. Возьмём и зафиксируем теперь какую-нибудь точку, принадлежа­щую Γ (они есть), и обозначим её через M ₀. Пусть её координаты суть (x ₀; y ₀; z ₀). Так как эта точка принадлежит Γ, для её координат справедливо соотношение:

Ax ₀ + By ₀ + Cz ₀ + D = 0. (1¢)

Вычитая из уравнения (1) равенство (1¢), мы получаем новое уравнение

A (x − x ₀) + B (y − y ₀) + C (z − z ₀) = 0, (1*)

очевидным образом равносильное уравнению (1) (т. к. мы можем вернуться к уравнению (1), прибавляя к уравнению (1*) равенство (1¢)). Значит, уравнение (1*) определяет то же самое множество Γ.

Возьмём теперь произвольную точку M = (x; y; z) из множества Γ и распишем ко­ординаты вектора :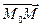

{ x − x ₀; y − y ₀; z − z ₀}.

Уравнение (1*) можно записать теперь так:

(n, 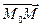) = 0. (3)

Это новое равенство (3) показывает нам, что точка M принадлежит множеству Γ тогда и только тогда, когда n ^ 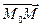. Обозначим через π плоскость, проходящую через точку M ₀ и перпендикулярную вектору n. Если точка M принадлежит множеству Γ, то n ^ ^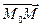. Прямая M ₀ M перпендикулярна вектору n и, следовательно, лежит в π. Значит, точка M лежит в π. Но, очевидно, верно и обратное, так что Γ = π, QED.

Следствие из теоремы. Уравнение плоскости, проходящей через точку с координа­тами (x ₀; y ₀; z ₀) и ортогональной данному ненулевому вектору с координатами { A; B; C }, имеет вид:

A (x − x ₀) + B (y − y ₀) + C (z − z ₀) = 0

(в двумерном случае уравнение прямой, проходящей через точку с координатами (x ₀; y ₀) и ортогональной данному ненулевому вектору с координатами { A; B }, есть A (x − x ₀) + B (y − − y ₀) = 0).

Примечания. 1. Заметим, что выполнение неравенства n ≠ 0 в условии теоремы существенно, ибо если n = 0, то в трёхмерном случае мы получим либо пустое множество (если D ≠ 0), либо всё пространство (если D = 0). Равным образом в двумерном случае по­лучим либо пустое множество (если C ≠ 0), либо всю плоскость (если C = 0).

2. Верно и обратное утверждение: любая плоскость в трёхмерном пространстве об­ладает уравнением вида (1), а любая прямая на плоскости − уравнением вида (2).

Доказательство (для трёхмерного случая). Возьмём произвольный вектор n = { A; B; C } ≠ 0, ортогональный данной плоскости, и произвольную точку M ₀ = (x ₀; y ₀; z ₀), ей принадлежащую. Рассмотрим уравнение (1*). По основной теореме оно определяет плос­кость, перпендикулярную вектору n. Очевидно также, что эта плоскость проходит через точку M ₀. Но такая плоскость единственна и совпадает с данной.

Определение. Уравнения (1) и (2) называются общими уравнениями соответст­венно плоскости и прямой.

Дата добавления: 2014-01-05