Поверхность уровня

Dx

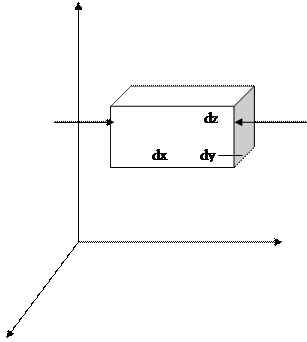
Основное дифференциальное уравнение равновесия жидкости.

Z

x

y

Рассмотрим жидкость находящуюся в состоянии равновесия. Выделим из нее бесконечно малый элемент в форме параллелепипеда. Рассмотрим давление, действующее по направлению оси Ч на элемент жидкости. Предположим, что в центре левой грани будет действовать давление ρ, тогда в центре правой грани будет действовать давление перпендикулярное этой грани и равное ρ + 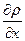dx.

Тогда сила давления, действующая на левую грянь равна:

р^лг = ρ●dy●dz; р^пг = (ρ + 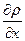dx) ●dy●dz.

Кроме того, на выделенный элемент жидкости будет действовать массовая сила в направлении оси ОХ:

М = ρ●dy●dz●Х,

где Х-проекция ускорения всех массовых сил на ось Ох.

Для того чтобы элемент находился в равновесии, сумма всех сил должна быть равна нулю.

ρ●dy●dz - (ρ + 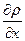dx) ●dy●dz + ρ●dy●dz●Х = 0.

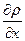●dx●dy●dz + ρ●dy●dz●Х = 0.

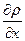-+ ρХ = 0. |dx

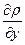-+ ρХ = 0. |dy

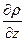-+ ρХ = 0. |dz

Получили систему дифференциальных уравнений равновесия жидкости Эйлера.

Она выражает в дифференциальной формуле закон распределения гидростатического давления, как несжимаемой капельной жидкости, так и сжимаемой. Для того, чтобы определить действие сил в направлении всех трех координатных осей умножим уравнения на dx, dy, dz соответственно и сложим:

dx + ρХ = 0.

+ dy + ρХ = 0.

dz + ρХ = 0

_____________

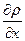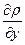dx + dy + 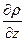dz = p (Xdx +Ydy +Zdz)

Так как гидростатическое давление зависит только от трех независимых переменных X, Y, Z, то левая части уравнения представляет собой сумму трех част. Дифференциалов

dρ=p (Xdx +Ydy +Zdz) – основное дифференциальное уравнение равновесия жидкостей.

Поверхность все точки, которой имеют одинаковое значение функции, называется поверхностью уровня.

Так поверхность жидкости с одинаковым давлением во всех ее точках называется поверхностью равного давления.

Поверхность, отделяющая жидкое тело от газообразной среду называется свободной поверхностью жидкости.

Из дифференциального уравнения Эйлера можно получить уравнение поверхности уровня в дифференциальной форме.

ρ = const;

dρ = 0;

p = const.

p (Xdx + Ydy + Zdz) = 0.

Xdx + Ydy + Zdz = 0.

Уравнение устанавливает связь между свободной поверхностью и действующими на жидкость объемными внешними силами, которые характеризуются ускорениями x, y, z.

Свойства поверхности уравнения:

1) Две различные поверхности не пересекаются между собой.

2) Объемные внешние силы направлены нормально к жидкости.

Дата добавления: 2014-01-05